Twierdzenie o maksymalnym przenoszeniu mocy
Ilość mocy pobieranej przez obciążenie jest ważnym parametrem w zastosowaniach elektrycznych i elektronicznych. W obwodach prądu stałego obciążenie możemy przedstawić za pomocą rezystora o rezystancji R L omów. Podobnie w obwodach prądu przemiennego możemy to przedstawić za pomocą złożonego obciążenia o impedancji Z L Ω.
Maximum power transfer theorem stwierdza, że źródło napięcia stałego będzie dostarczać maksymalną moc do rezystora zmiennego obciążenia tylko wtedy, gdy rezystancja obciążenia jest równa rezystancji źródła.
Podobnie, Maximum power transfer theorem stwierdza, że źródło napięcia prądu przemiennego będzie dostarczać maksymalną moc do zmiennego złożonego obciążenia tylko wtedy, gdy impedancja obciążenia jest równa złożonemu sprzężonemu impedancji źródła.
W tym rozdziale omówimy twierdzenie o maksymalnym przenoszeniu mocy dla obwodów prądu stałego.
Dowód twierdzenia o maksymalnym przenoszeniu mocy
Wymień dowolne dwa zaciski liniowej sieci lub obwodu po lewej stronie rezystora zmiennego obciążenia o rezystancji R L omów na równoważny obwód Thevenina. Wiemy, że równoważny obwód Thevenina przypomina praktyczne źródło napięcia.
Koncepcję tę zilustrowano na poniższych rysunkach.
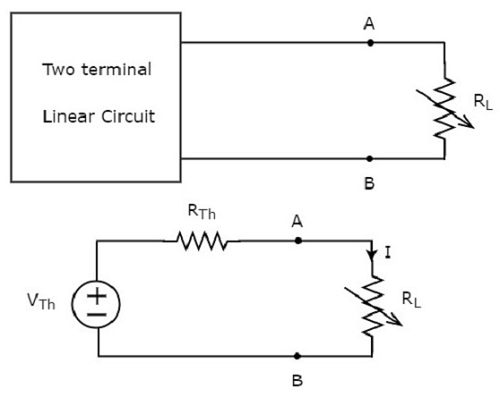
Ilość mocy rozproszonej na rezystorze obciążenia wynosi
$$ P_L = I ^ 2 R_L $$
Podstaw $ I = \ frac {V_ {Th}} {R_ {Th} + R_L} $ w powyższym równaniu.
$$ P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L $$
$ \ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L) ^ 2} \ rbrace $ Equation 1
Warunek maksymalnego transferu mocy
Dla maksimum lub minimum pierwsza pochodna będzie wynosić zero. Rozróżnij więc równanie 1 względem R L i zrób z niego zero.
$$ \ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L) ^ 2 \ times 1 - R_L \ times 2 (R_ {Th} + R_L) } {(R_ {Th} + R_L) ^ 4} \ rbrace = 0 $$
$$ \ Rightarrow (R_ {Th} + R_L) ^ 2 -2R_L (R_ {Th} + R_L) = 0 $$
$$ \ Rightarrow (R_ {Th} + R_L) (R_ {Th} + R_L - 2R_L) = 0 $$
$$ \ Rightarrow (R_ {Th} - R_L) = 0 $$
$$ \ Rightarrow R_ {Th} = R_L \: lub \: R_L = R_ {Th} $$
Dlatego też condition for maximum powerrozproszenie na obciążeniu wynosi $ R_L = R_ {Th} $. Oznacza to, że jeśli wartość rezystancji obciążenia jest równa wartości rezystancji źródła, czyli rezystancji Thevenina, wówczas moc rozpraszana na obciążeniu będzie miała wartość maksymalną.
Wartość maksymalnego transferu mocy
Podstaw $ R_L = R_ {Th} \: \ & \: P_L = P_ {L, Max} $ w równaniu 1.
$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th}) ^ 2} \ rbrace $$
$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}, \: od \: R_ {L} = R_ {Th} $$
Dlatego też maximum amount of power przeniesiony do obciążenia
$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} $$
Wydajność maksymalnego transferu mocy
Możemy obliczyć sprawność maksymalnego transferu mocy, $ \ eta_ {Max} $, używając następującego wzoru.
$ \ eta_ {Max} = \ frac {P_ {L, Max}} {P_S} $ Equation 2
Gdzie,
$ P_ {L, Max} $ to maksymalna ilość mocy przekazanej do obciążenia.
$ P_S $ to ilość energii generowanej przez źródło.
Plik amount of power generated według źródła
$$ P_S = I ^ 2 R_ {Th} + I ^ 2 R_L $$
$$ \ Rightarrow P_S = 2 I ^ 2 R_ {Th}, \: od \: R_ {L} = R_ {Th} $$
Podstaw $ I = \ frac {V_ {Th}} {2 R_ {Th}} $ w powyższym równaniu.
$$ P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th} $$
$$ \ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th} $$
$$ \ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th}} $$
Zastąp wartości $ P_ {L, Max} $ i $ P_S $ w Równaniu 2.
$$ \ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} { 2R_ {Th}} \ rgroup} $$
$$ \ Rightarrow \ eta_ {Max} = \ frac {1} {2} $$
Możemy przedstawić wydajność maksymalnego transferu mocy w kategoriach percentage w następujący sposób -
$$ \% \ eta_ {Max} = \ eta_ {Max} \ times 100 \% $$
$$ \ Rightarrow \% \ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ times 100 \% $$
$$ \ Rightarrow \% \ eta_ {Max} = 50 \% $$
Dlatego wydajność maksymalnego transferu mocy wynosi 50 %.
Przykład
Znaleźć maximum powerktóre można dostarczyć do rezystora obciążającego R L obwodu pokazanego na poniższym rysunku.
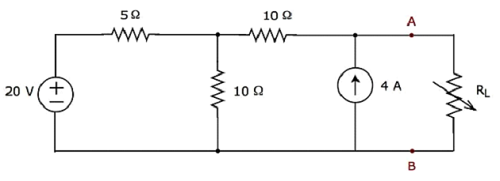
Step 1- W rozdziale Twierdzenie Thevenina obliczyliśmy obwód zastępczy Thevenina po lewej stronie zacisków A i B. Teraz możemy użyć tego obwodu. Przedstawiono to na poniższym rysunku.
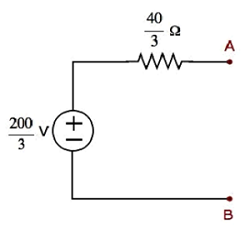
Tutaj napięcie Thevenina $ V_ {Th} = \ frac {200} {3} V $ i opór Thevenina $ R_ {Th} = \ frac {40} {3} \ Omega $
Step 2- Zamień część obwodu, która jest po lewej stronie zacisków A i B danego obwodu, na powyższy obwód zastępczy Thevenina. Powstały schemat obwodu pokazano na poniższym rysunku.

Step 3- Maksymalną moc, która zostanie dostarczona do rezystora obciążenia, R L, możemy znaleźć za pomocą następującego wzoru.
$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
Podstaw $ V_ {Th} = \ frac {200} {3} V $ i $ R_ {Th} = \ frac {40} {3} \ Omega $ w powyższym wzorze.
$$ P_ {L, Max} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup} $$
$$ P_ {L, Max} = \ frac {250} {3} W $$
Dlatego też maximum power który zostanie dostarczony do rezystora obciążenia RL danego obwodu to $ \ mathbf {\ frac {250} {3}} $ W