Macierze topologii sieci
W poprzednim rozdziale omówiliśmy, jak przekształcić obwód elektryczny w równoważny wykres. Omówmy teraz macierze topologii sieci, które są przydatne do rozwiązywania wszelkich problemów z obwodami elektrycznymi lub siecią przy użyciu ich równoważnych wykresów.
Macierze powiązane z wykresami sieci
Poniżej przedstawiono trzy macierze używane w teorii grafów.
- Macierz przypadków
- Podstawowa macierz pętli
- Matryca podstawowego zestawu cięcia
Macierz przypadków
Macierz incydentów przedstawia wykres danego obwodu elektrycznego lub sieci. W związku z tym możliwe jest narysowanie wykresu tego samego obwodu elektrycznego lub sieci z plikuincidence matrix.
Wiemy, że graf składa się ze zbioru węzłów, które są połączone niektórymi gałęziami. Tak więc łączenie gałęzi z węzłem nazywa się zdarzeniem. Macierz zachorowań jest oznaczona literą A. Jest również nazywana macierzą częstości od węzła do gałęzi lubnode incidence matrix.
Jeśli istnieje „n” węzłów, a gałęzie „b” są obecne w pliku directed graph, to macierz częstości będzie miała „n” wierszy i „b” kolumn. Tutaj wiersze i kolumny odpowiadają węzłom i gałęziom skierowanego wykresu. Stądorder macierzy zachorowań będzie n × b.
Plik elements of incidence matrix będzie mieć jedną z tych trzech wartości, +1, -1 i 0.
Jeśli prąd odgałęzienia wychodzi z wybranego węzła, to wartość elementu będzie wynosić +1.
Jeśli prąd rozgałęzienia wchodzi w kierunku wybranego węzła, to wartość elementu będzie wynosić -1.
Jeśli prąd rozgałęzienia nie dociera do wybranego węzła ani nie wychodzi z wybranego węzła, wówczas wartość elementu będzie wynosić 0.
Procedura znajdowania macierzy zdarzeń
Wykonaj poniższe kroki, aby znaleźć macierz częstości na wykresie skierowanym.
Wybierz węzeł w momencie danego wykresu skierowanego i wypełnij wartości elementów macierzy zdarzeń odpowiadających temu węzłowi w wierszu.
Powtórz powyższy krok dla wszystkich węzłów danego grafu skierowanego.
Przykład
Rozważ następujące directed graph.

Plik incidence matrix odpowiadający powyższemu skierowanemu wykresowi będzie
$$ A = \ begin {bmatrix} -1 & 1 & 0 & -1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 & -1 \ end {bmatrix} $$
Wiersze i kolumny powyższej macierzy reprezentują węzły i gałęzie danego grafu skierowanego. Rząd tej macierzy częstości wynosi 4 × 6.
Obserwując powyższą macierz zdarzeń, możemy stwierdzić, że summationkolumnowych elementów macierzy zdarzeń jest równa zeru. Oznacza to, że prąd odgałęzienia wychodzi z jednego węzła i wchodzi tylko do innego pojedynczego węzła.
Note- Jeśli dany wykres jest typu niekierowanego, zamień go na wykres skierowany, przedstawiając strzałki na każdej jego gałęzi. Możemy wziąć pod uwagę dowolny kierunek przepływu prądu w każdej gałęzi.
Podstawowa macierz pętli
Podstawowa pętla lub f-loopto pętla, która zawiera tylko jedno łącze i jedną lub więcej gałązek. Tak więc liczba pętli F będzie równa liczbie łączy. Podstawowa macierz pętli jest oznaczona literą B. Jest również nazywana asfundamental circuit matrixi macierz wiązana. Ta macierz podaje związek między prądami gałęzi i prądami łącza.
Jeśli istnieje „n” węzłów, a gałęzie „b” są obecne w pliku directed graph, wówczas liczba linków występujących w współdrzewie, które odpowiada wybranemu drzewu danego wykresu, będzie wynosić b-n + 1.
Zatem podstawowa macierz pętli będzie miała wiersze „b-n + 1” i kolumny „b”. Tutaj wiersze i kolumny odpowiadają połączeniom ko-drzewa i gałęzi danego wykresu. Stąd kolejność podstawowej macierzy pętli będzie(b - n + 1) × b.
Plik elements of fundamental loop matrix będzie mieć jedną z tych trzech wartości, +1, -1 i 0.
Wartość elementu będzie wynosić +1 dla łącza wybranej pętli F.
Wartość elementów będzie wynosić 0 dla pozostałych linków i gałązek, które nie są częścią wybranej pętli F.
Jeżeli kierunek prądu gałązki wybranej pętli f jest taki sam jak kierunek prądu łącza f-pętli, to wartość elementu będzie wynosić +1.
Jeżeli kierunek prądu gałązki wybranej pętli f jest przeciwny do kierunku prądu łącza pętli f, to wartość elementu będzie wynosić -1.
Procedura znajdowania podstawowej macierzy pętli
Wykonaj poniższe kroki, aby znaleźć podstawową macierz pętli danego wykresu skierowanego.
Wybierz drzewo danego wykresu skierowanego.
Dołączając jedno łącze na raz, otrzymamy jedną pętlę F. Wypełnij wartości elementów odpowiadających tej pętli f w wierszu podstawowej macierzy pętli.
Powtórz powyższy krok dla wszystkich linków.
Przykład
Spójrz na następujące drzewo directed graph, który jest brany pod uwagę w przypadku macierzy zdarzeń.

Powyższe drzewo zawiera trzy gałęzie d, e i f. W związku z tym gałęzie a, b i c będą połączeniami drzewa wspólnego odpowiadającego powyższemu drzewu. Dołączając po jednym linku do powyższego drzewa, otrzymamy jedenf-loop. Tak więc będą trzyf-loops, ponieważ istnieją trzy linki. Te trzy pętle F pokazano na poniższym rysunku.
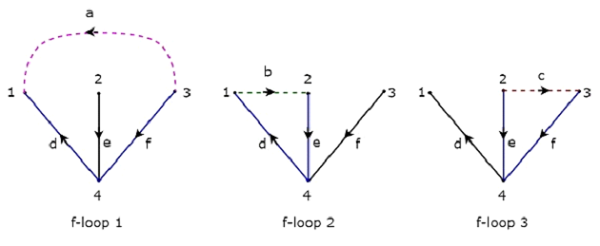
Na powyższym rysunku gałęzie, które są przedstawione kolorowymi liniami, tworzą pętle F. Otrzymamy wartości elementów dla wierszy macierzy typu Tie-set z każdej pętli f. Tak więcTieset matrix z powyższego drzewa będzie
$$ B = \ begin {bmatrix} 1 & 0 & 0 & -1 & 0 & -1 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & -1 & 1 \ end {bmatrix} $$
Wiersze i kolumny powyższej macierzy reprezentują łącza i gałęzie danego skierowanego wykresu. Kolejność tej macierzy częstości to 3 × 6.
Plik number of Fundamental loop matriceswykresu skierowanego będzie równa liczbie drzew tego wykresu skierowanego. Ponieważ każde drzewo będzie miało jedną podstawową macierz pętli.
Podstawowa macierz zestawów cięć
Zestaw do cięcia podstawowego lub f-cut setjest minimalną liczbą gałęzi, które są usuwane z wykresu w taki sposób, że oryginalny wykres stanie się dwoma izolowanymi podgrafami. Zestaw f-cut zawiera tylkoone twigi co najmniej jeden link. Tak więc liczba zestawów ciętych w kształcie litery F będzie równa liczbie gałązek.
Fundamental cut set matrix jest oznaczona literą C. Ta macierz podaje zależność między napięciami gałęzi i napięciami gałęzi.
Jeśli istnieje „n” węzłów, a gałęzie „b” są obecne w pliku directed graph, to liczba gałązek obecnych w wybranym Drzewie danego wykresu wyniesie n-1. Zatem podstawowa macierz zbioru cięć będzie miała wiersze „n-1” i kolumny „b”. Tutaj rzędy i kolumny odpowiadają gałązkom wybranego drzewa i gałęziom danego wykresu. Stądorder podstawowej macierzy zestawu cięć będzie (n-1) × b.
Plik elements of fundamental cut set matrix będzie mieć jedną z tych trzech wartości, +1, -1 i 0.
Wartość elementu wyniesie +1 dla gałązki wybranego zbioru f-cut.
Wartość elementów będzie wynosić 0 dla pozostałych gałązek i ogniw, które nie są częścią wybranego zbioru f-cut.
Jeżeli kierunek prądu łącza wybranego zestawu f-cut jest taki sam jak kierunek prądu f-cut set twig, to wartość elementu będzie wynosić +1.
Jeżeli kierunek prądu łącza wybranego zestawu f-cut jest przeciwny do kierunku prądu f-cut set twig, to wartość elementu będzie wynosić -1.
Procedura znajdowania podstawowej macierzy zestawów cięć
Wykonaj poniższe kroki, aby znaleźć podstawową macierz zbioru cięć dla danego skierowanego wykresu.
Wybierz drzewo danego skierowanego wykresu i przedstaw łącza liniami przerywanymi.
Usuwając po jednej gałązce i niezbędnych ogniwach na raz, otrzymamy jeden zestaw f-cut. Wypełnij wartości elementów odpowiadających temu zestawowi f-cut w wierszu podstawowej macierzy zestawu cięć.
Powtórz powyższy krok dla wszystkich gałązek.
Przykład
Rozważ to samo directed graph , które omówiliśmy w sekcji macierzy częstości. Wybierz gałęzie d, e i f tego skierowanego wykresu jako gałązki. Zatem pozostałe gałęzie a, b i c tego skierowanego wykresu będą linkami.
Plik twigs d, e i f są przedstawiane liniami ciągłymi i links a, b i c są przedstawione liniami przerywanymi na poniższym rysunku.
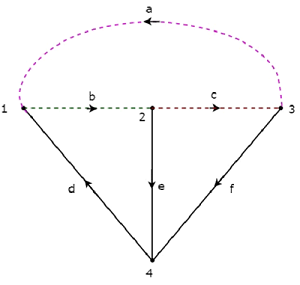
Usuwając po jednej gałązce i niezbędnych ogniwach na raz, otrzymamy jeden zestaw f-cut. Tak więc będą trzy zestawy cięć typu F, ponieważ są trzy gałązki. Ta trójkaf-cut sets pokazano na poniższym rysunku.

Będziemy mieć trzy zestawy f-cut, usuwając zestaw gałązek i ogniw C 1 , C 2 i C 3 . Otrzymamy wartości elementów w wierszach podstawowej macierzy zbioru cięć z każdego zbioru f-cut. Tak więcfundamental cut set matrix z powyższego drzewa będzie
$$ C = \ begin {bmatrix} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \ end {bmatrix} $$
Wiersze i kolumny powyższej macierzy reprezentują gałązki i gałęzie danego skierowanego wykresu. Kolejność tej podstawowej macierzy zbioru cięć wynosi 3 × 6.
Plik number of Fundamental cut set matriceswykresu skierowanego będzie równa liczbie drzew tego wykresu skierowanego. Ponieważ każde drzewo będzie miało jedną macierz podstawowego zestawu cięć.