Rozumowanie - zakodowane liczby binarne
Liczba o podstawie 2 jest znana jako liczba binarna. Liczbę binarną tworzą komplementy zera i jedynki. Zatem zakodowana liczba binarna składa się z dwóch procesów. Jedna to konwersja liczby dwójkowej na dziesiętną, a druga to konwersja dziesiętna na dwójkową.
Liczby dziesiętne
Wiedzieć co binary numberjest to, że najpierw musimy wiedzieć o liczbach dziesiętnych. Tak więc liczba dziesiętna składa się z dziesięciu cyfr (tj. 0,1,2,3,4,5,6,7,8,9). Za pomocą tych liczb można przedstawić dowolny system dziesiętny. Na przykład ciąg cyfr to 2, 4, 6 i 8. Robimy to w następujący sposób -
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- Wartość liczb otrzymujemy w tym przypadku mnożąc różne cyfry ciągu przez potęgi 10 i dodając. Tutaj ta 10 nazywa się podstawą lub radixem. Dlatego w systemie dziesiętnym naszą podstawą jest 10.
Liczby binarne
Używamy dziesięciu cyfr do reprezentacji decimal number; w ten sposób używamy tylko dwóch cyfr do przedstawienia liczby binarnej. Dowolną liczbę można przedstawić za pomocą tych dwóch cyfr, tj. 0 i 1.
Przykład liczby binarnej to - 1101. Tutaj występują 4 cyfry w ciągu cyfr - 1, 1, 0, 1. Wartość otrzymujemy w następujący sposób.
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
Zatem liczba binarna reprezentuje trzynaście w systemie dziesiętnym. Wartość można określić za pomocąmultiplying different digits sekwencji przez potęgę 2 i dodawanie.
Conventional method - W powyższym przykładzie widzimy, że aby uzyskać wartość dowolnej liczby binarnej, używamy następującej reguły -
Pierwsza cyfra od prawej jest mnożona przez 2 0 = 1
Druga cyfra od prawej jest mnożona przez 2 1 = 2
Trzecia cyfra od prawej jest mnożona przez 2 2 = 4
Podobnie n- ta cyfra od prawej jest mnożona przez 2 n − 1
Wreszcie wszystkie te są dodane.
For Example - Zamień następujące liczby binarne na liczby dziesiętne.
A - 1010
B - 1111
C - 100
D - 10000
Solution -
A - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
B - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
C - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
D - 10000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
Szybsza metoda
Step I- Rozpoczynając od prawej cyfry podanej liczby wpisz 1, 2, 4, 8, 16, 32 ……. i tak dalej pod każdą cyfrą, idąc w lewo.
Step II- Zignoruj liczby poniżej zera. Dodaj wszystkie liczby poniżej 1s.
Rozwiążmy przykład 1 tą metodą.
A - 1010
Użyjemy 1, 2, 4, 8, ponieważ obecne są tutaj 4 cyfry.
Otrzymujemy,
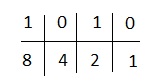
4 i 1 wypadają poniżej zer. Ignorujemy je i dodajemy pozostałe. Otrzymujemy 8 + 2 = 10
W ten sposób możemy rozwiązać inne liczby.
Liczbę dziesiętną można przekonwertować na binarną metodą successive divisions. Za każdym razem dywidenda jest dzielona przez 2. Przypomnienie jest odnotowywane, a iloraz staje się kolejną dywidendą, która jest ponownie dzielona przez 2. Proces jest powtarzany, aż dalsze dzielenie nie jest możliwe.
Na przykład - zamień 17 na liczbę binarną -
Podziel 17 przez 2, dopóki nie będzie już możliwe.
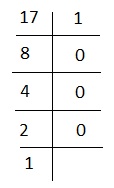
Tak więc binarna forma liczby 17 to 10001.
Direction (Q. 1-4) − Study the following question and give the answer.
W pewnym kodzie symbol 0 to +, a 1 to #. Żadna liczba ani symbol nie jest większa niż 1. Wartość symbolu za 1 podwaja się za każdym razem, gdy przesuwa się o jedno miejsce w lewo.
„0” jest przedstawiane jako +
„1” jest przedstawiane jako #
„2” jest przedstawiane jako # +
„3” jest przedstawiane jako ##
„4” jest przedstawiane jako # ++ i tak dalej
1 - Które z poniższych będzie reprezentować 11?
Options -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - żaden z tych
Answer - Opcja A
Explanation - Aby otrzymać odpowiednik 11, stosujemy metodę sukcesywnego dzielenia przez 2.

Zatem forma binarna będzie wynosić 10111. Zamieniając 1 i 0 na # i + otrzymamy # + ##.
2 - Które z poniższych będzie reprezentować 8?
Options -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - żaden z tych
Answer - Wariant E.
Explanation - na 8 mamy-
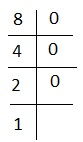
czyli 1000 lub # +++. Prawidłowy wybór to 5.
3 - Które z poniższych będą reprezentowane przez ## + #?
Options -
A - 8
B - 11
C - 13
D - 12
E - żaden z tych
Answer - Wariant E.
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 15
4 - Która z poniższych liczb będzie reprezentowana przez # +++ #?
Options -
A - 22
B - 31
C - 14
D - 17
E - żaden z tych
Answer - Opcja D
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
Systemy binarne mają podstawę 2, system dziesiętny ma podstawę 10, a trzeciorzędny ma podstawę 3, a ósemkowy podstawę 8. W przypadku trzeciorzędu mamy trzy cyfry do reprezentacji liczb. Są to 0, 1 i 2. W tym przypadku liczby zostaną zamienione na dziesiętne poprzez pomnożenie ich przez odpowiednie potęgi 3.
For Example -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3