Rozumowanie - logiczna dedukcja
Logiczna dedukcja jest ważnym rozdziałem, ponieważ wiele łatwych i dających ocenę pytań z tego rozdziału jest zawartych w różnych egzaminach konkursowych. W tym rozdziale omówimy dwie metody rozwiązywania takich problemów -
- Metoda sylogizmu
- Metoda diagramu Venna
Podstawy
Jeśli istnieją dwa stwierdzenia, to sylogizm będzie najlepszym sposobem rozwiązania problemu, ale jeśli liczba zdań jest większa niż dwa, wybierz metodę diagramu Venna. Czasami stwierdzenia i wnioski wypływają z ogólnie przyjętych faktów, ale mogą też być nielogiczne. Na przykład -
a) Niektóre krzesła są drzwiami.
b) Wszyscy mężczyźni są kobietami
c) Żadne mleko nie jest białe
Aby dojść do wniosku, potrzebne jest myślenie abstrakcyjne. Trzeba zrozumieć logiczny sens zdania, a następnie odpowiednio odpowiedzieć na wnioski. Każde stwierdzenie musi być uważane za prawdziwe, a następnie musimy zweryfikować, czy wnioski są logicznie zgodne ze stwierdzeniami.
Kwalifikatory
Oto niektóre z podstawowych słów, które są używane do opisania, jak bardzo jedna rzecz jest podobna lub różni się od drugiej. Przykładami niektórych kwalifikatorów są „Wszystkie”, „Niektóre”, „Niektóre - nie” itp.
Koncepcja diagramu Venna
Z drugiej strony diagram Venna to proces, w którym możemy przedstawić zdanie lub stwierdzenie w postaci figur geometrycznych. Wszystkie podane stwierdzenia są przedstawione na możliwych diagramach Venna. Następnie wszystkie wnioski są weryfikowane za pomocą tych diagramów. Każdy wniosek, który spełnia wszystkie diagramy Venna, będzie uznany za ważny wniosek.
| Sprawozdania | Odpowiadające diagramy Venna |
|---|---|
| Wszystkie A są B. |
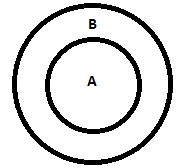
|
| Niektóre A to B (LUB) Niektóre A nie są B. |
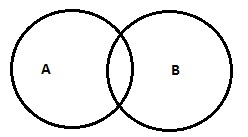
|
| Nie A to B |
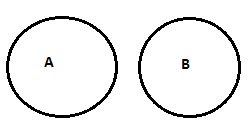
|
Weźmy prosty przykład, aby lepiej to zrozumieć.
Sample − 1
Statements -
Wszyscy inżynierowie są głupcami. Wszyscy głupcy są lekarzami. Wszyscy lekarze są biedni.
Conclusions -
I. Niektórzy biedni są głupcami.
II. Niektórzy biedni to inżynierowie.
Options -
A - Tylko ja jest ważny
B - Tylko II jest ważny
C - Oba oświadczenia są ważne
D - Żadne z oświadczeń nie jest ważne
Answer - Opcja C
Explanation -
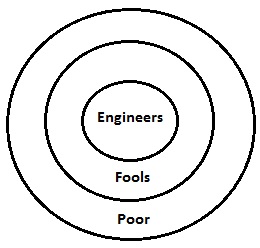
Diagram Venna dla podanych stwierdzeń został przedstawiony powyżej. Pokazuje wszystkie stwierdzenia w formie schematu w jednym miejscu. Tutaj teraz, jeśli omówimy kolejno wnioski o konkluzjach, wszystko będzie jasne.
Tutaj głupcy są podzbiorem biednych. Jest więc oczywistym faktem, że niektórzy biedni będą głupcami. Stąd wniosek I jest ważny. Podobnie wniosek II jest ważny, ponieważ inżynierowie są również podzbiorem ubogich. Dlatego oba oświadczenia będą ważne.
Sample − 2
Statements -
Niektóre klawiatury to mysz. Niektóre myszy to radia.
Conclusions -
I. Niektóre klawiatury to radia.
II. Niektóre radia to klawiatury
III. Wszystkie radia to mysz.
IV. Wszystkie myszy to klawiatury.
Options -
A - Jedyny wniosek I jest ważny
B - Jedyny wniosek II jest ważny
C - Ważny jest I lub II
D - Żaden z wniosków nie jest ważny
E - Oba I i II są ważne
Answer - Opcja D
Explanation - Ponieważ oba stwierdzenia są szczególne, żaden ostateczny wniosek nie jest ważny.
Sample − 3
Statements -
Wszyscy uczniowie są trzeźwi. Wszyscy uczniowie są niegrzeczni.
Conclusions -
I. Wszyscy niegrzeczni są albo trzeźwi, albo odwrotnie.
II. Niektóre trzeźwe osoby są niegrzeczne.
III. Ogólnie niegrzeczni są trzeźwi.
IV. Zbrodnia i poczucie winy idą w parze.
Options -
A - Jedyny wniosek I jest ważny
B - Jedyny wniosek II jest ważny
C - Ważny jest I lub II
D - Żaden z I ani II nie jest ważny
E - Oba I i II są ważne
Answer - Wariant B.
Explanation- Ponieważ średniookresowy termin „studenci” występuje w oświadczeniach dwukrotnie, wniosek nie może być szeroki. Tak więc jest ważne, że „Niektóre osoby trzeźwe są niegrzeczne”. Tak więc, II jest prawdą.