Brakujące znaki - rozwiązane przykłady
Pytanie 1 -
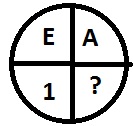
Options :
A - 5
B - 2
C - 3
D - 4
Answer - A
Explanation
W porządku alfabetycznym „A” to jeden, podczas gdy E to 5.
Pytanie 2 -
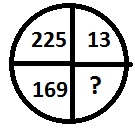
Options :
A - 9
B - 11
C - 15
D - 12
Answer - C
Explanation
Liczby mają swój kwadrat w przestrzeni po przekątnej.
Pytanie 3 -
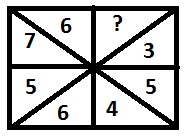
Options :
A - 2
B - 9
C - 5
D - 8
Answer - D
Explanation
Liczby zmieniają się w kierunku zgodnym z ruchem wskazówek zegara, jak przez dodawanie 2 i odejmowanie 1 na przemian, zaczynając od 3. Stąd brakująca liczba to 8.
Pytanie 4 -
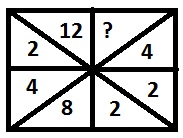
Options :
A - 7
B - 9
C - 6
D - 8
Answer - C
Explanation
Połowa poprzedniej liczby jest umieszczana na kolejnym polu, a 2 zajmuje miejsce po każdych dwóch krokach.
Pytanie 5 -
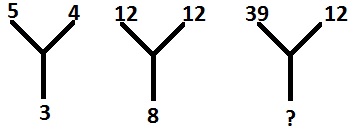
Options :
A - 15
B - 17
C - 19
D - 21
Answer - B
Explanation
Liczbę na dole otrzymuje się jako $ \ frac {5 + 4} {3} = 3 $ i $ \ frac {12 + 12} {3} = 8 $, podobnie $ \ frac {12 + 39} {3 } = 17 $. Dlatego brakująca liczba to 17.
Pytanie 6 -
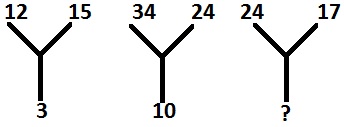
Options :
A - 4
B - 9
C - 11
D - 7
Answer - D
Explanation
Liczby na dole to różnica liczb na górze, dlatego brakująca liczba to 24-17 = 7.
Pytanie 7 -
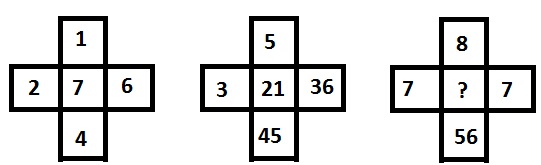
Options :
A - 5
B - 7
C - 8
D - 12
Answer - C
Explanation
Liczby są otrzymywane jako $ \ frac {4} {1} + \ frac {6} {2} = 7 $ i $ \ frac {45} {5} + \ frac {36} {3} = 21 $, podobnie $ \ frac {7} {7} + \ frac {56} {8} = 8 $.
Pytanie 8 -
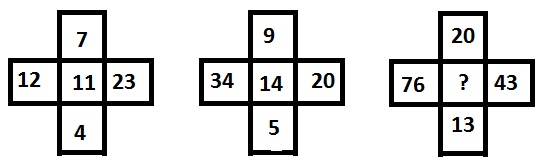
Options :
A - 25
B - 14
C - 62
D - 33
Answer - D
Explanation
Liczby są powiązane jako 23 - 12 = 11 = 7 + 4 i 34 - 20 = 14 = 9 + 5, podobnie 76 - 43 = 33 = 20 + 13.
P 9 -

Options :
A - 68
B - 89
C - 85
D - 90
Answer - C
Explanation
Liczby otrzymujemy jako, 2 2 + 5 2 = 29 i 1 2 +3 2 = 10, dlatego brakująca liczba to 7 2 + 6 2 = 85.
P 10 -
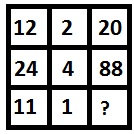
Options :
A - 14
B - 18
C - 23
D - 12
Answer - D
Explanation
Oczywiste jest, że 12 + 2 3 = 20 i 24 + 4 3 = 88, w ten sposób 11 + 1 3 = 12.