Rozumowanie - sylogizm

Znaczenie sylogizmu podane przez Greków jest takie Deduction. To rodzaj logicznej argumentacji.

Definicja niektórych ważnych terminów

Poniżej podano kilka terminów, które odgrywają ważną rolę w rozwiązywaniu problemów sylogizmu.

• Proposition- zdanie to zdanie składające oświadczenia. Zdanie składa się z 3 części: a) podmiot, b) orzeczenie ic) relacja między podmiotem a orzeczeniem. Poniżej podano kilka propozycji.

  • Wszystkie wybrzeża to plaże.
  • Żaden uczeń nie jest uczciwy.
  • Niektóre dokumenty są tajne.

• Subject and Predicate- Temat to ta część, o której coś się mówi. Z drugiej strony predykat jest częścią związaną z podmiotem. Na przykład - z powyższych propozycji wybrzeża, studenci, dokumenty są przedmiotami, a plaże, uczciwość i tajemnica są predykatami.

Typy zdań kategorialnych

• Universal Proposition- Zdaniem uniwersalnym jest to, co obejmuje przedmiot w całości lub całkowicie go wyklucza. Na przykład - żaden uczeń nie jest bystry. Propozycja uniwersalna jest dalej podzielona na następujące -

  • Universal positive proposition - Kiedy jest formularz all X are Ywtedy nazywa się to twierdzeniem pozytywnym. Zwykle jest oznaczony literąA.

  • Universal negative proposition - Kiedy jest formularz no X are T, wtedy nazywa się to twierdzeniem negatywnym. Jest oznaczonyE.

• Particular proposition- To propozycja częściowo ukazuje temat lub częściowo go wyklucza, ale nie całkowicie. Na przykład niektóre koty są bawełniane. Jest również podzielony na następujące typy -

  • Particular positive proposition - Formy jak some X are Unazywane są szczególnie pozytywną propozycją. Są zakodowane jakoI.

  • Particular negative proposition - Formy jak Some T are not P na przykład, some cats are not coils nazywany jest szczególnym zdaniem negatywnym i zakodowany jako O.

• Mediate inference- Tutaj wniosek pochodzi z dwóch stwierdzeń. Przykład - „wszystkie usta to cewki” i „wszystkie piłki to nietoperze”. Zatem wniosek będzie taki, że „wszystkie wargi są cewkami”.

• Immediate inference- Tutaj wniosek zostanie wyciągnięty tylko z jednej propozycji. Na przykład, jeśli stwierdzenie brzmi: „wszyscy nauczyciele są bogami”, wniosek będzie brzmiał: „niektórzy nauczyciele są bogami”.

Dwie ważne metody natychmiastowego wnioskowania

Metody te obejmują konwersję, kontrapozycję itp.

• Implications- Przypuśćmy, że „wszystkie koty to plaże”, to pokazuje, że wniosek „niektóre koty to plaże” jest prawdziwy. Jeśli więc dane zdanie należy do kategorii A, to pokazuje również, że wniosek typu I musi być prawdziwy.

• Conversion - Składa się z 2 stopni.

  Step 1 - Podmiot zostanie przekształcony w orzeczenie i odwrotnie.

  Step 2 - Podana propozycja zostanie odpowiednio zmieniona.

For Example −

Statements- Wszystkie koty to stojaki. Wszystkie torby są stojakami. Niektóre torebki to torby.

Conclusions -

1. Niektóre koty to torby.

2. Niektóre stojaki to koty.

3. Niektóre stojaki to torebki.

A - Tylko 1

B - Tylko 2 i 3

C - Tylko 1 i 2

D - Tylko 1 i 3

Solution −

Odpowiedź - Wariant B.

Obrazowy sposób przedstawiania propozycji formułuje Euler. Istnieją cztery sposoby, na jakie można by ustanowić relację według czterech zdań.

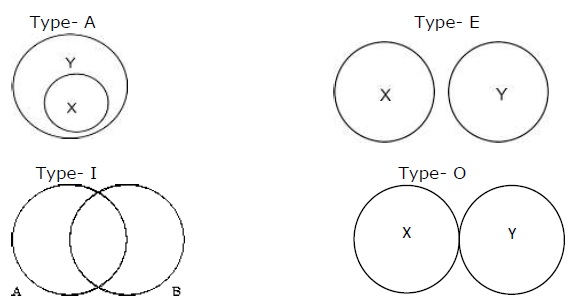
Type - A oznacza „All X are Y”, Type - E oznacza „No X are Y”, Type - I oznacza „Some A are B”, and Type - O oznacza „Some X are not Y”.

For Example −

Statements −

Niektóre aparaty to laptopy.

Niektóre laptopy to telefony.

Niektóre telefony to tablety.

Conclusions −

Ja - przynajmniej niektóre tablety to aparaty

II - Istnieje możliwość, że wszystkie tablety to laptopy

III - Żaden z tabletów nie jest laptopem

Solution −

Schemat koła -

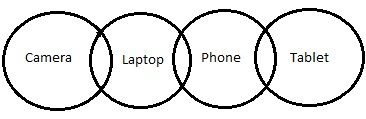
Jak na powyższym schemacie,

Wniosek III następuje. Ale słowo „możliwość” zostało wspomniane w oświadczeniu. Sprawdźmy więc możliwości.

Nowy diagram będzie -

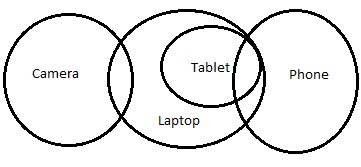
Ale w tym przypadku wniosek III nie wynika. Następuje konkluzja II lub konkluzja III.