Cosmologia - Guia Rápido

Cosmologyé o estudo do universo. Remontando no tempo, havia várias escolas de pensamentos sobre a origem do universo. Muitos estudiosos acreditaram noSteady State Theory. De acordo com essa teoria, o universo foi sempre o mesmo, não teve começo.

Embora houvesse um grupo de pessoas que tinham fé no Big Bang Theory. Esta teoria prevê o início do universo. Houve evidências de radiação quente deixada de fora do Big Bang, o que novamente apóia o modelo. A Teoria do Big Bang prevê a abundância de elementos leves no universo. Assim, seguindo o famoso modelo do Big Bang, podemos afirmar que o universo teve um início. Estamos vivendo em um universo em expansão.

O Hubble Redshift

No início de 1900, o telescópio de última geração, Mt Wilson, um telescópio de 100 polegadas, era o maior telescópio então. Hubble foi um dos cientistas proeminentes que trabalhou com aquele telescópio. Ele descobriu que havia galáxias fora da Via Láctea.Extragalactic Astronomytem apenas 100 anos. Mt Wilson foi o maior telescópio até que o Observatório Palmer foi construído, que tinha um telescópio de 200 polegadas.

Hubblenão foi a única pessoa a observar galáxias fora da Via Láctea, Humason o ajudou. Eles começaram a medir os espectros de galáxias próximas. Eles então observaram que um espectro galáctico estava na faixa de comprimento de onda visível com emissão contínua. Havia linhas de emissão e absorção no topo do continuum. A partir dessas linhas, podemos fazer uma estimativa se a galáxia está se afastando de nós ou em nossa direção.

Quando obtemos um espectro, assumimos que a linha mais forte vem de H-α. Da literatura, a linha mais forte deve ocorrer em6563 Å, mas se a linha ocorrer em algum lugar ao redor 7000Å, podemos facilmente dizer que ele está desviado para o vermelho.

De Special Theory of Relativity,

$$ 1 + z = \ sqrt {\ frac {1+ \ frac {v} {c}} {1- \ frac {v} {c}}} $$

onde, Z é o desvio para o vermelho, um número adimensional ev é a velocidade de recessão.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {rest}} = 1 + z $$

Hubble e Humason listados abaixo 22 Galaxiesem seu papel. Quase todas essas galáxias exibiram deslocamento para o vermelho. Eles traçaram a velocidade (km / s) vs distância (Mpc). Eles observaram uma tendência linear e Hubble apresentou sua famosa lei da seguinte maneira.

$$ v_r = H_o d $$

Isto é o Hubble Redshift Distance Relationship. O subscritorindica que a expansão está na direção radial. Enquanto $ v_r $ é a velocidade de recuo, $ H_o $ é o parâmetro do Hubble,dé a distância da galáxia de nós. Eles concluíram que galáxias distantes se afastam mais rapidamente de nós, se a taxa de expansão do universo for uniforme.

A expansão

Tudo está se afastando de nós. As galáxias não são estacionárias, há sempre algum harmônico de expansão. As unidades do parâmetro Hubble são km seg ⁻¹ Mpc ⁻¹ . Se alguém sair a uma distância de -1 Mpc, as galáxias estariam se movendo a uma taxa de 200 kms / s. O parâmetro Hubble nos dá a taxa de expansão. De acordo com Hubble e Humason, o valor de $ H_o $ é 200 kms / seg / Mpc.

Os dados mostraram que todas as galáxias estão se afastando de nós. Assim, é evidente que estamos no centro do universo. Mas Hubble não cometeu esse erro, segundo ele, em qualquer galáxia em que vivêssemos, encontraríamos todas as outras galáxias se afastando de nós. Assim, a conclusão é que o espaço entre as galáxias se expande e não há centro no universo.

A expansão está acontecendo em todos os lugares. No entanto, existem algumas forças que se opõem à expansão. Ligações químicas, força gravitacional e outras forças atrativas mantêm os objetos unidos. Anteriormente, todos os objetos estavam próximos. Considerando o Big Bang como uma força impulsiva, esses objetos são configurados para se afastarem uns dos outros.

Escala de tempo

Em escalas locais, a cinemática é governada pela gravidade. Na lei de Hubble original, havia algumas galáxias que exibiam deslocamento para o azul. Isso pode ser creditado ao potencial gravitacional combinado das galáxias. A gravidade separou as coisas da lei de Hubble. A Galáxia de Andrômeda está vindo em nossa direção. A gravidade está tentando desacelerar as coisas. Inicialmente, a expansão foi desacelerando, agora está se acelerando.

Havia um Cosmic JerkPor causa disso. Várias estimativas para o parâmetro de Hubble foram feitas. Evoluiu ao longo dos 90 anos de 500 kms / seg / Mpc para 69 kms / seg / Mpc. A disparidade no valor se deve à subestimação da distância. oCepheid Stars foram utilizados como calibradores de distância, porém existem diferentes tipos de estrelas Cefeidas e este fato não foi considerado para a estimativa do parâmetro de Hubble.

Hora de Hubble

A constante de Hubble nos dá uma estimativa realista da idade do universo. O $ H_o $ daria a idade do universo, desde que as galáxias tenham se movido com a mesma velocidade. O inverso de $ H_o $ nos dá o tempo de Hubble.

$$ t_H = \ frac {1} {H_o} $$

Substituindo o valor presente de $ H_o, t_H $ = 14bilhões de anos. A taxa de expansão foi constante ao longo do início do Universo. Mesmo que isso não seja verdade, $ H_o $ fornece um limite útil para a idade do universo. Assumindo uma taxa constante de expansão, quando traçamos um gráfico entre distância e tempo, a inclinação do gráfico é dada pela velocidade.

Nesse caso, o tempo de Hubble é igual ao tempo real. No entanto, se o universo estava se expandindo mais rápido no passado e mais lentamente no presente, o tempo de Hubble fornece um limite superior de idade do universo. Se o universo estava se expandindo lentamente antes, e acelerando agora, o tempo de Hubble dará um limite inferior para a idade do universo.

• $ t_H = t_ {idade} $ - se a taxa de expansão for constante.

• $ t_H> t_ {idade} $ - se o universo se expandiu mais rápido no passado e mais devagar no presente.

• $ t_H <t_ {idade} $ - se o universo se expandiu mais lentamente no passado e mais rápido no presente.

Considere um grupo de 10 galáxias que estão a 200 Mpc de outro grupo de galáxias. As galáxias dentro de um aglomerado nunca concluem que o universo está se expandindo porque a cinemática dentro de um grupo local é governada pela gravitação.

Pontos para lembrar

• Cosmologia é o estudo do passado, presente e futuro do nosso Universo.

• Nosso universo tem 14 bilhões de anos.

• O universo está se expandindo continuamente.

• O parâmetro Hubble é uma medida da idade do universo.

• Valor atual de H_o é 69 kms / seg / Mpc.

Por muito tempo, ninguém considerou que as galáxias estivessem presentes fora de nossa Via Láctea. Em 1924, Edwin Hubble detectouCepheid’sna Nebulosa de Andrômeda e estimou sua distância. Ele concluiu que essas "Nebulosas Espirais" eram na verdade outras galáxias e não uma parte de nossa Via Láctea. Portanto, ele estabeleceu que M31 (Galáxia de Andrômeda) é um universo insular. Este foi o nascimento deExtragalactic Astronomy.

Cefeida mostra um periodic dip in their brightness. As observações mostram que o período entre mergulhos sucessivos denominado período de pulsações está relacionado à luminosidade. Portanto, eles podem ser usados ​​como indicadores de distância. As estrelas da sequência principal, como o Sol, estão em equilíbrio hidrostático e queimam hidrogênio em seu núcleo. Depois que o hidrogênio é totalmente queimado, as estrelas se movem em direção à fase de gigante vermelho e tentam recuperar o equilíbrio.

As estrelas cefeidas são estrelas pós-sequência principal que estão transitando das estrelas da sequência principal para os gigantes vermelhos.

Classificação das cefeidas

Existem 3 grandes classes dessas estrelas variáveis ​​pulsantes -

• Type-I Cepheids (ou Cefeidas Clássicas) - período de 30-100 dias.

• Type-II Cepheids (ou W Virginis Stars) - período de 1 a 50 dias.

• RR Lyrae Stars - período de 0,1-1 dia.

Naquela época, o Hubble não tinha conhecimento dessa classificação de estrelas variáveis. É por isso que houve uma superestimativa da constante de Hubble, por causa da qual ele estimou uma idade inferior do nosso universo. Portanto, a velocidade da recessão também foi superestimada. Nas Cefeidas, os distúrbios se propagam radialmente para fora do centro da estrela até que o novo equilíbrio seja alcançado.

Relação entre Brilho e Período de Pulsação

Vamos agora tentar entender a base física do fato de que um período de pulsação mais alto implica mais brilho. Considere uma estrela de luminosidade L e massa M.

Nós sabemos disso -

$$ L \ propto M ^ \ alpha $$

onde α = 3 a 4 para estrelas de baixa massa.

De Stefan Boltzmann Law, nós sabemos disso -

$$ L \ propto R ^ 2 T ^ 4 $$

E se R é o raio e $ c_s $ é a velocidade do som, então o período de pulsação P pode ser escrito como -

$$ P = R / c_s $$

Mas a velocidade do som através de qualquer meio pode ser expressa em termos de temperatura como -

$$ c_s = \ sqrt {\ frac {\ gamma P} {\ rho}} $$

Aqui, γ é 1 para casos isotérmicos.

Para um gás ideal, P = nkT, onde k é o Boltzmann Constant. Então, podemos escrever -

$$ P = \ frac {\ rho kT} {m} $$

onde $ \ rho $ é a densidade e m é a massa de um próton.

Portanto, o período é dado por -

$$ P \ cong \ frac {Rm ^ {\ frac {1} {2}}} {(kT) ^ {{\ frac {1} {2}}}} $$

Virial Theorem afirma que, para uma distribuição esférica estável, autogravitante e de objetos de massa igual (como estrelas, galáxias), a energia cinética total k do objeto é igual a menos a metade da energia potencial gravitacional total u, ou seja,

$$ u = -2k $$

Vamos supor que o teorema virial seja verdadeiro para essas estrelas variáveis. Se considerarmos um próton bem na superfície da estrela, então, a partir do teorema virial, podemos dizer -

$$ \ frac {GMm} {R} = mv ^ 2 $$

Da distribuição Maxwell,

$$ v = \ sqrt {\ frac {3kT} {2}} $$

Portanto, ponto final -

$$ P \ sim \ frac {RR ^ {\ frac {1} {2}}} {(GM) ^ {\ frac {1} {2}}} $$

que implica

$$ P \ propto \ frac {R ^ {\ frac {3} {2}}} {M ^ {\ frac {1} {2}}} $$

Nós sabemos que - $ M \ propto L ^ {1 / \ alpha} $

Também $ R \ propto L ^ {1/2} $

Então, para β > 0, finalmente obtemos - $ P \ propto L ^ \ beta $

Pontos para lembrar

• As estrelas cefeidas são estrelas pós-sequência principal que estão transitando das estrelas da sequência principal para os gigantes vermelhos.

• As cefeidas são de 3 tipos: Tipo I, Tipo II, RR-Lyrae em ordem decrescente de período pulsante.

• O período de pulsação da Cefeida é diretamente proporcional ao seu brilho (luminosidade).

As observações de Hubble fizeram uso do fato de que a velocidade radial está relacionada ao deslocamento do Spectral Lines. Aqui, observaremos quatro casos e encontraremos uma relação entre a velocidade de recessão ($ v_r $) e o desvio para o vermelho (z).

Caso 1: Caso Não Relativístico de Mudança de Fonte

Nesse caso, v é muito menor que c. A fonte está emitindo algum sinal (som, luz, etc.), que está se propagando conformeWavefronts. O intervalo de tempo entre o envio de dois sinais consecutivos no quadro fonte éΔts. O intervalo de tempo entre a recepção de dois sinais consecutivos no quadro do observador éΔto.

Se o observador e a fonte estiverem estacionários, então Δts = Δto, mas este não é o caso aqui. Em vez disso, a relação é a seguinte.

$$ \ Delta t_o = \ Delta t_s + \ frac {\ Delta l} {c} $$

Agora, $ \ Delta l = v \ Delta t_s $

Além disso, uma vez que (velocidade da onda x tempo) = comprimento de onda, obtemos

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ lambda_o} {\ lambda_s} $$

A partir das equações acima, obtemos a seguinte relação -

$$ \ frac {\ lambda_o} {\ lambda_s} = 1 + \ frac {v} {c} $$

onde $ \ lambda _s $ é o comprimento de onda do sinal na fonte e $ \ lambda _o $ é o comprimento de onda do sinal interpretado pelo observador.

Aqui, uma vez que a fonte está se afastando do observador, v é positivo.

Mudança para o vermelho -

$$ z = \ frac {\ lambda_o - \ lambda_s} {\ lambda_s} = \ frac {\ lambda_o} {\ lambda_s} - 1 $$

A partir das equações acima, obtemos o deslocamento para o vermelho da seguinte maneira.

$$ z = \ frac {v} {c} $$

Caso 2: Caso Não Relativístico de Movimento do Observador

Nesse caso, v é muito menor que c. Aqui, $ \ Delta l $ é diferente.

$$ \ Delta l = v \ Delta t_o $$

Na simplificação, obtemos -

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ left (1 - \ frac {v} {c} \ right) ^ {- 1} $$

Obtemos o turno para o vermelho da seguinte forma -

$$ z = \ frac {v / c} {1-v / c} $$

Desde a v << c, a expressão de desvio para o vermelho para o Caso I e o Caso II são aproximadamente iguais.

Vejamos como os desvios para o vermelho obtidos nos dois casos acima diferem.

$$ z_ {II} - z_I = \ frac {v} {c} \ left [\ frac {1} {1 - v / c} -1 \ right] $$

Portanto, $ z_ {II} - z_ {I} $ é um número muito pequeno devido ao fator $ (v / c) ^ 2 $.

Isso implica que, se v << c, não podemos dizer se a fonte está se movendo ou se o observador está se movendo.

Vamos agora entender o Basics of STR (Teoria da Relatividade Especial) -

• A velocidade da luz é uma constante.

• Quando a fonte (ou observador) está se movendo a uma velocidade comparável à velocidade da luz, efeitos relativísticos são observados.

• Dilatação do tempo: $ \ Delta t_o = \ gamma \ Delta t_s $

• Contração de comprimento: $ \ Delta l_o = \ Delta t_s / \ gamma $

• Aqui, $ \ gamma $ é o Lorrentz factor, maior que 1.

$$ \ gamma = \ frac {1} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

Caso 3: Caso Relativístico de Mudança de Fonte

Nesse caso, v é comparável a c. Consulte a mesma figura do Caso I. Devido ao efeito relativístico, a dilatação do tempo é observada e, portanto, a seguinte relação é obtida. (A fonte está se movendo com velocidade relativística)

$$ \ Delta t_o = \ gamma \ Delta t_s + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ gamma \ Delta t_s} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {1 + v / c} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

Em uma simplificação adicional, obtemos,

$$ 1 + z = \ sqrt {\ frac {1 + v / c} {1-v / c}} $$

A expressão acima é conhecida como Kinematic Doppler Shift Expression.

Caso 4: Caso Relativístico de Movimento do Observador

Consulte a mesma figura do Caso II. Devido ao efeito relativístico, o encurtamento do tempo é observado e, portanto, a seguinte relação é obtida. (O observador está se movendo com velocidade relativística)

$$ \ Delta t_o = \ frac {\ Delta t_s} {\ gamma} + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ Delta t_o} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ sqrt {1- (v ^ 2 / c ^ 2)}} {1-v / c} $$

Para simplificar ainda mais, obtemos -

$$ 1 + z = \ sqrt {\ frac {1+ v / c} {1- v / c}} $$

A expressão acima é a mesma que obtivemos para o Caso III.

Pontos para lembrar

• A velocidade de recessão e o desvio para o vermelho de uma estrela são quantidades relacionadas.

• Em um caso não relativístico, não podemos determinar se a fonte está em movimento ou estacionária.

• Em um caso relativístico, não há diferença na relação redshift-velocidade recessional para o movimento da fonte ou do observador.

• Os relógios em movimento se movem mais devagar, é um resultado direto da teoria da relatividade.

Uma galáxia que está em deslocamento para o vermelho z = 10, corresponde a v≈80% do c. A massa da Via Láctea está ao redor1011M⊙, se considerarmos a matéria escura, é 1012M⊙. Nossa Via Láctea é, portanto, massiva. Se ele se mover a 80% dec, não se encaixa no conceito geral de como os objetos se movem.

Nós sabemos,

$$ \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda {rest}} {\ lambda_ {rest}} $$

Para pequenos valores de z,

$$ z = \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda_ {rest}} {\ lambda_ {rest}} $$

No gráfico a seguir, a classe entre fluxo e comprimento de onda, existem linhas de emissão no topo do continuum. DeH-α informações de linha, podemos concluir que aproximadamente z = 7. Isso implica que a galáxia está se movendo a 70% dec. Estamos observando uma mudança e interpretando-a como velocidade. Devemos nos livrar dessa noção e olhar parazde uma maneira diferente. Imagine o espaço como uma grade 2D representando o universo, conforme mostrado abaixo.

Considere a estrela negra como nossa própria Via Láctea e a estrela azul como alguma outra galáxia. Quando registramos a luz desta galáxia, vemos o espectro e descobrimos seu desvio para o vermelho, ou seja, a galáxia está se afastando. Quando o fóton foi emitido, ele tinha velocidade relativa.

• E se o espaço estivesse se expandindo?

• É um desvio para o vermelho instantâneo do fóton. Redshifts cumulativos ao longo do espaço entre duas galáxias tenderão a um grande redshift. O comprimento de onda mudará finalmente. É a expansão do espaço, e não o movimento cinemático das galáxias.

A imagem a seguir mostra se a gravidade mútua transborda a expansão, então isso não está participando da lei de Hubble.

No Doppler Shift cinemático, o desvio para o vermelho é induzido em um fóton no momento da emissão. Em um Redshift cosmológico, em cada etapa, ele está ficando cumulativamente redshift. Em um potencial gravitacional, um fóton ficará azul deslocado. À medida que sai do potencial gravitacional, ele é desviado para o vermelho.

De acordo com a Teoria da Relatividade Especial, dois objetos que passam um pelo outro não podem ter uma velocidade relativa maior do que a velocidade da luz. A velocidade de que falamos é da expansão do universo. Para grandes valores de z, o redshift é cosmológico e não uma medida válida da velocidade recessional real do objeto em relação a nós.

O Princípio Cosmológico

Origina-se do Copernicus NotionDo universo. De acordo com essa noção, o universo é homogêneo e isotrópico. Não há direção e localização preferenciais no universo.

• Homogeneidade significa que não importa em que parte do universo você reside, você verá que o universo é o mesmo em todas as partes. Natureza isotrópica significa que não importa para qual direção você olhe, você verá a mesma estrutura.

• Um exemplo adequado de homogeneidade é um campo de arroz. Parece homogêneo em todas as partes, mas quando o vento flui, há variações em sua orientação, portanto, não é isotrópico. Considere uma montanha em um terreno plano e um observador está parado no topo da montanha. Ele verá a natureza isotrópica da terra plana, mas não é homogênea. Se em um universo homogêneo, é isotrópico em um ponto, é isotrópico em todos os lugares.

• Tem havido pesquisas em grande escala para mapear o universo. Sloan Digital Sky Surveyé uma dessas pesquisas, que não se concentrou muito na declinação, mas na ascensão reta. O tempo de lookback é de cerca de 2 bilhões de anos. Cada pixel corresponde à localização de uma galáxia e a cor corresponde à estrutura morfológica. A cor verde representava a galáxia espiral azul, enquanto a falsa cor vermelha indicava galáxias massivas.

• As galáxias estão em uma estrutura filamentar em uma teia cosmológica e existem vazios entre as galáxias.

• $ \ delta M / M \ cong 1 $ ie, a flutuação da distribuição da massa é 1 M é a massa da matéria presente dentro de um dado cubo. Neste caso, pegue o cubo de 50 Mpc de volume.

• Para um lado do cubo de 1000 Mpc, $ \ delta M / M \ cong 10 ^ {- 4} $.

• Uma maneira de quantificar a homogeneidade é considerar as flutuações de massa. As flutuações de massa serão maiores em escalas inferiores.

• Para quantificar a natureza isotrópica, considere a radiação cósmica de fundo em microondas. O Universo é quase isotrópico em grandes escalas angulares.

Pontos para lembrar

• Dois objetos passando um pelo outro não podem ter uma velocidade relativa maior do que a velocidade da luz.

• O Princípio Cosmológico afirma que o universo é homogêneo e isotrópico.

• Essa homogeneidade existe em uma escala angular muito grande e não em escalas menores.

• SDSS (Sloan Digital Sky Survey) é um esforço para mapear o céu noturno, verificando o Princípio Cosmológico.

De acordo com a lei da conservação da energia e a lei da conservação da massa, a quantidade total de energia incluindo a massa (E = mc ² ) permanece inalterada em todas as etapas de qualquer processo no universo. A expansão do próprio universo consome energia que pode ser do alongamento do comprimento de onda dos fótons (Cosmological Redshift), interações de energia escura, etc.

Para acelerar o levantamento de mais de 26.000 galáxias, Stephen A. Shectmanprojetou um instrumento capaz de medir 112 galáxias simultaneamente. Em uma placa de metal, furos que correspondiam às posições das galáxias no céu foram perfurados. Cabos de fibra óptica transportavam a luz de cada galáxia para um canal separado em um espectrógrafo no telescópio du Pont de 2,5 metros noCarnegie Observatories no Cerro Las Campanas, no Chile.

Para máxima eficiência, uma técnica especializada conhecida como Drift-Scan Photometryfoi usado, no qual o telescópio foi apontado para o início de um campo de pesquisa e, em seguida, o acionamento automatizado foi desligado. O telescópio ficou parado enquanto o céu passava. Os computadores lêem as informações doCCD Detectorno mesmo ritmo da rotação da Terra, produzindo uma imagem longa e contínua em uma latitude celestial constante. A conclusão da fotometria levou um total de 450 horas.

Existem diferentes formas de ruído e sua modelagem matemática é diferente dependendo de suas propriedades. Vários processos físicos desenvolvem o espectro de energia do universo em grande escala. O espectro de potência inicial transmitido devido às flutuações quânticas segue uma terceira potência negativa de frequência, que é uma forma dePink Noise Spectrum em três dimensões.

The Metric

Em cosmologia, deve-se primeiro ter uma definição de espaço. Uma métrica é uma expressão matemática que descreve pontos no espaço. A observação do céu é feita em uma geometria esférica; portanto, um sistema de coordenadas esféricas deve ser usado. A distância entre dois pontos próximos é dada por -

$$ ds ^ 2 = dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 $$

A imagem a seguir mostra a geometria no espaço euclidiano não expansível tridimensional.

Esta geometria ainda está no espaço euclidiano não expansível tridimensional. Conseqüentemente, a grade de referência que define o próprio quadro estaria se expandindo. A imagem a seguir mostra o aumento da métrica.

Um fator de escala é colocado na equação do espaço não expansível, chamado de 'fator de escala', que incorpora a expansão do universo em relação ao tempo.

$$ ds ^ 2 = a ^ 2 (t) \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $$

Onde a(t) é o fator de escala, às vezes escrito como R(t). Enquanto que,a(t) > 1 significa ampliação da métrica, enquanto a(t) < 1 significa encolhimento da métrica e a(t) = 1significa métrica constante. Por convenção,a(t₀) = 1.

Sistema de Coordenadas Comoving

Em um Comoving Coordinate System, a escala de medição se expande junto com a estrutura (universo em expansão).

Aqui, $ \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $ é a distância de movimento e $ ds ^ 2 $ é o Distância adequada.

A distância adequada corresponderá à distância real medida de uma galáxia distante da Terra no momento da observação, também conhecida como distância instantânea de objetos.

Isso ocorre porque a distância percorrida por um fóton ao atingir o observador de uma fonte distante será a recebida em $ t = t_0 $ do observador, o que significaria que a distância instantânea observada será a distância adequada, e pode-se prever distâncias futuras usando o fator de taxa e o comprimento medido inicial como referência.

O conceito de Comoving e distância adequada é importante para medir o valor real da densidade numérica de galáxias em um determinado volume do espaço observado. Deve-se usar a distância de comovente para calcular a densidade no momento de sua formação quando o fóton observado foi emitido. Isso pode ser obtido uma vez que a taxa de expansão do universo possa ser estimada.

Para estimar a taxa de expansão, pode-se observar a mudança na distância de uma galáxia distante observada durante um longo período de tempo.

Pontos para lembrar

• Uma métrica é uma expressão matemática que descreve os pontos no espaço.

• O fator de escala determina se o universo está se contraindo ou se expandindo.

• Em um sistema de coordenadas móvel, a escala de medição se expande junto com a estrutura (universo em expansão).

• A distância adequada é a distância instantânea dos objetos.

• A distância comovente é a distância real dos objetos.

Neste capítulo, vamos entender em detalhes sobre a métrica Robertson-Walker.

Modelo para mudança de fator de escala com o tempo

Suponha que um fóton seja emitido de uma galáxia distante. O espaço é avançado para o fóton em todas as direções. A expansão do universo está em todas as direções. Vamos ver como o fator de escala muda com o tempo nas etapas a seguir.

Step 1 - Para um universo estático, o fator de escala é 1, ou seja, o valor da distância comovente é a distância entre os objetos.

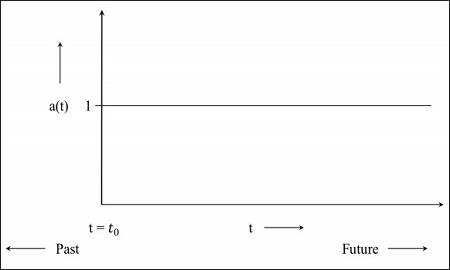
Step 2- A imagem a seguir é o gráfico do universo que ainda está se expandindo, mas em uma taxa decrescente, o que significa que o gráfico começará no passado. ot = 0 indica que o universo começou a partir desse ponto.

Step 3 - A imagem a seguir é o gráfico do universo que está se expandindo em um ritmo mais rápido.

Step 4 - A imagem a seguir é o gráfico do universo que começa a se contrair a partir de agora.

Se o valor do fator de escala se torna 0 durante a contração do universo, isso implica que a distância entre os objetos torna-se 0, ou seja, a distância adequada torna-se 0. A distância comovente, que é a distância entre os objetos no universo atual, é uma quantidade constante. No futuro, quando o fator de escala se tornar0, tudo vai chegar mais perto. O modelo depende do componente do universo.

A métrica para o universo em expansão plano (euclidiano: não há parâmetro para curvatura) é dada como -

$$ ds ^ 2 = a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) $$

Para espaço-tempo, o elemento de linha que obtivemos na equação acima é modificado como -

$$ ds ^ 2 = c ^ 2dt ^ 2 - \ left \ {a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ direita) \ right \} $$

Para o espaço-tempo, o momento em que o fóton é emitido e quando é detectado é diferente. A distância adequada é a distância instantânea aos objetos, que pode mudar com o tempo devido à expansão do universo. É a distância que o fóton percorreu de diferentes objetos para chegar até nós. Está relacionado à distância comovente como -

$$ d_p = a (t) \ vezes d_c $$

onde $ d_p $ é a distância apropriada e $ d_c $ é a distância de movimento, que é fixa.

A distância medida para os objetos no universo atual é considerada como a distância comovente, o que significa que a distância comovente é fixa e não é alterada pela expansão. No passado, o fator de escala era menor que 1, o que indica que a distância adequada era menor.

Podemos medir o desvio para o vermelho de uma galáxia. Portanto, a distância apropriada $ d_p $ corresponde a $ c \ times t (z) $, onde $ t (z) $ é o tempo de lookback para um redshift ec é a velocidade da luz no vácuo. O tempo de lookback é uma função do redshift(z).

Com base na noção acima, vamos analisar como o desvio cosmológico para o vermelho é interpretado neste cenário de $ d_p = a (t) \ times d_c $.

Suponha que um fóton (que está ligado à Terra) seja emitido pela galáxia, G. O $ t_ {em} $ corresponde ao momento em que o fóton foi emitido; $ a (t_ {em}) $ era o fator de escala no momento em que o fóton foi emitido. No momento da detecção do fóton, todo o universo havia se expandido, ou seja, o fóton foi desviado para o vermelho no momento da detecção. O $ t_ {obs} $ corresponde ao momento em que o fóton é detectado e o fator de escala correspondente é $ a (t_ {obs}) $.

O fator pelo qual o universo cresceu é dado por -

$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$

O fator pelo qual o comprimento de onda se expandiu é -

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

que é igual ao fator pelo qual o universo cresceu. Os símbolos têm seu significado usual. Portanto,

$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

Nós conhecemos aquele desvio para o vermelho (z) é -

$$ z = \ frac {\ lambda_ {obs} - \ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} - 1 $$

$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$

O valor presente do fator de escala é 1, portanto $ a (t_ {obs}) = 1 $ e denotando o fator de escala quando o fóton foi emitido no passado por $ a (t) $.

Portanto,

$$ 1 + z = \ frac {1} {a (t)} $$

Interpretação do Redshift na Cosmologia

Para entender isso, tomemos o seguinte exemplo: Se $ z = 2 $, então $ a (t) = 1/3 $.

Isso implica que o universo se expandiu por um fator de três desde que a luz deixou aquele objeto. O comprimento de onda da radiação recebida se expandiu por um fator de três porque o espaço se expandiu pelo mesmo fator durante seu trânsito do objeto emissor. Deve-se notar que em valores tão grandes dez, o redshift é principalmente o redshift cosmológico e não é uma medida válida da velocidade recessional real do objeto em relação a nós.

Para fundo cósmico de microondas (CMB), z = 1089, o que significa que o universo atual se expandiu por um fator de ∼1090. A métrica para o universo plano e euclidiano em expansão é dada como -

$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$

Queremos escrever a métrica em qualquer curvatura.

Robertson and Walker provado para qualquer universo de curvatura (que é homogêneo e isotrópico), a métrica é dada como -

$$ ds ^ 2 = a ^ 2 (t) \ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$

Isso geralmente é conhecido como Robertson–Walker Metrice é verdadeiro para qualquer topologia de espaço. Observe o fator extra em $ dr ^ 2 $. Aqui é a constante de curvatura.

Geometria do Universo

A Geometria do Universo é explicada com a ajuda das seguintes Curvaturas, que incluem -

• Curvatura Positiva
• Curvatura Negativa
• Curvatura Zero

Vamos entender cada um deles em detalhes.

Curvatura Positiva

Se um plano tangente desenhado em qualquer ponto da superfície da curvatura não se cruza em nenhum ponto da superfície, é denominado superfície com curvatura positiva, isto é, a superfície permanece em um lado do plano tangente naquele ponto. A superfície da esfera tem curvatura positiva.

Curvatura Negativa

Se um plano tangente desenhado em um ponto da superfície da curvatura se cruza em qualquer ponto da superfície, ele é chamado de superfície com curvatura negativa, isto é, as curvas da superfície afastam-se do plano tangente em duas direções diferentes. Uma superfície em forma de sela tem uma curvatura negativa.

Agora considere a superfície de uma esfera. Se um triângulo é construído na superfície da esfera unindo três pontos com geodésico (arco de grandes círculos), a soma dos ângulos internos do triângulo esférico é maior que 180 ^o , ou seja -

$$ \ alpha + \ beta + \ gamma> \ pi $$

Esses espaços são chamados de espaços positivamente curvos. Além disso, a curvatura é homogênea e isotrópica. Em geral, o ângulo nos vértices do triângulo esférico segue a relação -

$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$

Onde A é a área do triângulo e Ré o raio da esfera. A imagem a seguir descreve um espaço positivamente curvo.

Para uma curvatura positiva, as linhas paralelas devem se encontrar. Considere a superfície da Terra, que é um espaço positivamente curvo. Pegue dois pontos de partida no equador. As linhas que cruzam o equador em ângulos retos são conhecidas como linhas de longitude. Uma vez que essas linhas cruzam o equador em ângulos retos, podem ser chamadas de linhas paralelas. Começando no equador, eles eventualmente se cruzam nos pólos. Este método foi usado porCarl Gauss e outros para compreender a topologia da Terra.

Considere um espaço curvado negativamente (uma sela mostrada na imagem a seguir), a soma dos ângulos internos do triângulo é menor que 180 ^o , ou seja -

$$ \ alpha + \ beta + \ gamma <\ pi $$

O ângulo nos vértices segue a relação -

$$ \ alpha + \ beta + \ gamma = \ pi - A / R ^ 2 $$

Curvatura Zero

Uma superfície plana tem curvatura zero. Agora, para um espaço plano, se um plano for tomado e um triângulo for construído unindo três pontos com geodésicos (linhas retas), a soma interna dos ângulos será -

$$ \ alpha + \ beta + \ gamma = \ pi $$

A imagem a seguir é um espaço bidimensional plano.

Se alguém quiser que um espaço seja homogêneo e isotrópico, apenas três possibilidades permanecem: o espaço pode ser uniformemente plano ou pode ter uma curvatura positiva uniforme ou pode ter uma curvatura negativa uniforme.

A constante de curvatura pode assumir qualquer um dos três valores a seguir.

$$ k = \ begin {cases} +1, & para \: a \: positivamente \: curvo \: espaço; \\\ quad 0, & para \: a \: plano \: espaço; \\ - 1, & para \: a \: negativamente \: curvo \: espaço; \ end {casos} $$

Topologia Global do Universo

O universo tem uma determinada topologia, mas localmente pode ter rugas. Dependendo de como a matéria se distribui no espaço, há variações menores na curvatura. Vamos supor que haja uma classe de objetos que têm o mesmo tamanho verdadeiro, não importa onde esteja no universo, o que significa que eles são como velas padrão. Eles não têm o mesmo brilho, mas têm o mesmo tamanho.

Se o objeto estiver em um espaço positivamente curvo e os fótons vierem do ponto A (uma extremidade do objeto) e B (outra extremidade do objeto), os fótons se propagarão paralelamente no espaço positivamente curvo através do caminho geodésico e eventualmente se encontrarão . Para um observador em C, parecerá que veio de dois pontos diferentes em direções diferentes.

Se o objeto está no universo local e medimos o tamanho angular, ele não é afetado pela curvatura. Se a mesma classe de objeto for vista em um redshift maior, o tamanho angular não se correlaciona com.

$$ \ theta = \ frac {d} {r} $$

Onde d é o tamanho do objeto e ré a distância ao objeto, ou seja, se o tamanho for maior que o tamanho local, significa que a curvatura é positiva. A imagem a seguir é uma representação do fóton detectado em um espaço positivamente curvo.

Deve-se notar que não existe um objeto astrofísico real de tamanho e morfologia padrão. Embora um cD elíptico massivo - galáxias fossem consideradas adequadas às velas padrão, descobriu-se que também estavam evoluindo com o tempo.

Encontrando distâncias para galáxias

Nesta seção, discutiremos como encontrar a distância até uma galáxia levando em consideração a imagem a seguir.

Considere a Via Láctea em (r, θ,) em um referencial de repouso cosmológico. Pode-se pegar = 0; (0, θ, ϕ), ou seja, o centro do universo invocando a suposição de homogeneidade.

Considere uma galáxia 'G' em (r1, θ,). A distância (adequada) é a distância radial mais curta percorrida por um fóton. Pela simetria do espaço - tempo, a geodésica nula de r = 0 a r = r1, tem uma direção constante no espaço. Em sua propagação radial, as coordenadas angulares não mudam. Se as coordenadas angulares forem alteradas, então este não é o caminho mais curto. Essa é a razão pela qual o termo curvatura está presente no dr ² .

Pontos para lembrar

• A expansão do universo está em todas as direções.

• O universo pode ser estático, em expansão ou contração, dependendo da evolução do fator de escala.

• As galáxias cD evoluem com o tempo e, portanto, não podem ser usadas como velas padrão.

• O universo tem certa topologia, mas localmente pode ter rugas.

Neste capítulo, discutiremos sobre o parâmetro de Hubble, bem como o fator de escala.

• Prerequisite - Cosmological Redshift, Cosmological Principles.

• Assumption - O universo é homogêneo e isotrópico.

Constante de Hubble com taxa fracional de mudança do fator de escala

Nesta seção, relacionaremos a constante de Hubble com a taxa fracionária do fator de mudança de escala.

Podemos escrever velocidade da seguinte maneira e simplificar.

$$ v = \ frac {\ mathrm {d} r_p} {\ mathrm {d} t} $$

$$ = \ frac {d [a (t) r_c} {dt} $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast (ar_c) $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast r_p $$

Aqui, v é a velocidade recessiva, a é o fator de escala e r_p é a distância adequada entre as galáxias.

Hubble’s Empirical Formula era da natureza -

$$ v = H \ ast r_p $$

Assim, comparando as duas equações acima, obtemos -

Hubble’s Parameter = Fractional rate of change of the scale factor

$$ H = da / dt \ ast 1 / a $$

Note- Esta não é uma constante, pois o fator de escala é uma função do tempo. Por isso é chamado de parâmetro de Hubble e não de constante de Hubble.

Empiricamente nós escrevemos -

$$ H = V / D $$

Assim, a partir desta equação, podemos inferir que uma vez que D está aumentando e V é uma constante, então H diminui com o tempo e a expansão do universo.

Equação de Friedmann em conjunção com o modelo Robertson-Walker

Nesta seção, entenderemos como a Equação de Friedmann é usada em conjunto com o modelo de Robertson-Walker. Para entender isso, vamos tirar a seguinte imagem, que tem uma massa de teste à distânciar_p do corpo de massa M como um exemplo.

Levando em consideração a imagem acima, podemos expressar força como -

$$ F = G \ ast M \ ast \ frac {m} {r ^ 2_p} $$

Aqui, G é a constante gravitacional universal e ρ é a densidade da matéria dentro do universo observável.

Agora, assumindo densidade de massa uniforme dentro da esfera, podemos escrever -

$$ M = \ frac {4} {3} \ ast \ pi \ ast r_p ^ 3 \ ast \ rho $$

Usando isso de volta em nossa equação de força, obtemos -

$$ F = \ frac {4} {3} \ ast \ pi \ ast G \ ast r_p \ ast \ rho \ ast m $$

Assim, podemos escrever a energia potencial e a energia cinética da massa m como -

$$ V = - \ frac {4} {3} \ ast \ pi \ ast G \ ast r ^ 2_p \ ast m \ ast \ rho $$

$$ KE = \ frac {1} {2} \ ast m \ ast \ frac {\ mathrm {d} r_p ^ 2} {\ mathrm {d} t} $$

Usando o Virial Theorem -

$$ U = KE + V $$

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} r_p} {\ mathrm {d} t} \ right) ^ 2 - \ frac {4} { 3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Mas aqui, $ r_p = ar_c $. Então, nós temos -

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} a} {\ mathrm {d} t} \ right) ^ 2 r_c ^ 2 - \ frac { 4} {3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Em uma simplificação posterior, obtemos a equação de Friedmann,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ ast G \ ast \ rho + \ frac {2U} {m} \ ast r_c ^ 2 \ ast a ^ 2 $$

Aqui Ué uma constante. Também notamos que o universo em que vivemos atualmente é dominado pela matéria, enquanto a densidade de energia da radiação é muito baixa.

Pontos para lembrar

• O parâmetro Hubble diminui com o tempo e a expansão do universo.

• O universo em que vivemos atualmente é dominado pela matéria e a densidade da energia da radiação é muito baixa.

Neste capítulo, entenderemos o que é a Equação de Friedmann e estudaremos detalhadamente os Modelos de Mundo para diferentes constantes de curvatura.

Equação de Friedmann

Essa equação nos fala sobre a expansão do espaço em modelos homogêneos e isotrópicos do universo.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {2U} {mr_c ^ 2a ^ 2} $ $

Isso foi modificado no contexto de General Relativity (GR) e Robertson-Walker Metric como segue.

Usando equações GR -

$$ \ frac {2U} {mr_c ^ 2} = -kc ^ 2 $$

Onde ké a constante de curvatura. Portanto,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} $ $

Além disso, $ \ rho $ é substituído por densidade de energia que inclui matéria, radiação e qualquer outra forma de energia. Mas, para fins de representação, é escrito como $ \ rho $.

Modelos mundiais para diferentes constantes de curvatura

Vejamos agora as várias possibilidades dependendo dos valores da constante de curvatura.

Caso 1: k = 1, ou universo fechado

Para um universo em expansão, $ da / dt> 0 $. Conforme a expansão continua, o primeiro termo no RHS da equação acima vai como $ a ^ {- 3} $, enquanto o segundo termo vai como $ a ^ {- 2} $. Quando os dois termos se tornam iguais, o universo para de expansão. Então -

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {kc ^ 2} {a ^ 2} $$

Aqui, k = 1, portanto,

$$ a = \ left [\ frac {3c ^ 2} {8 \ pi G \ rho} \ right] ^ {\ frac {1} {2}} $$

Esse universo é finito e possui volume finito. Isso é chamado de Universo Fechado.

Caso 2: k = -1 ou Universo aberto

E se k < 0, a expansão nunca pararia. Depois de algum tempo, o primeiro termo no RHS pode ser negligenciado em comparação com o segundo termo.

Aqui, k = -1. Portanto, $ da / dt ∼ c $.

Nesse caso, o universo está parando. Esse universo tem espaço e tempo infinitos. Isso é chamado de Universo aberto.

Caso 3: k = 0 ou Universo plano

Nesse caso, o universo está se expandindo em uma taxa decrescente. Aqui, k = 0. Portanto,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho $$

Esse universo tem espaço e tempo infinitos. Isso é chamado de Universo plano.

Pontos para lembrar

• A equação de Friedmann nos fala sobre a expansão do espaço em modelos homogêneos e isotrópicos do universo.

• Dependendo dos diferentes valores da constante de curvatura, podemos ter um Universo Fechado, Aberto ou Plano.

Neste capítulo, discutiremos a equação do fluido e como ela nos diz a respeito da densidade do universo que muda com o tempo.

Estimando ρ _c e ρ no Universo Presente

Para o universo presente -

$$ \ rho_c \ simeq 10 ^ {11} M_ \ odot M_ {pc} ^ {- 3} \ simeq 10 \: hidrogênio \: átomos \: m ^ {- 3} $$

Existe toda uma gama de densidade crítica em nosso espaço sideral. Por exemplo, para o meio intergaláctico $ \ rho_c $ é 1 átomo de hidrogênio $ m ^ {- 3} $, enquanto que para nuvens moleculares é $ 10 ^ 6 $ átomos de hidrogênio $ m ^ {- 3} $.

Devemos medir $ \ rho_c $ considerando amostras adequadas de espaço. Dentro de nossa galáxia, o valor de $ \ rho_c $ é muito alto, mas nossa galáxia não é uma representante de todo o universo. Portanto, devemos ir para o espaço onde o princípio cosmológico se mantém, ou seja, distâncias ≈ 300 Mpc. Olhar para 300 Mpc significa olhar 1 bilhão de anos atrás, mas ainda é o universo presente.

Pesquisas como o SDSS são conduzidas para determinar a densidade real da matéria. Eles pegam um volume de 5 × 500 × 5 Mpc ³ , contam o número de galáxias e somam toda a luz proveniente dessas galáxias. Supondo que 1 L ≡ 1 M, ou seja, 1 luminosidade solar ≡ 1 massa solar.

Fazemos uma conversão de luz em massa e então tentamos estimar o número de bárions com base nas partículas de matéria visível presentes naquele volume.

Por exemplo,

$$ 1000L_ \ odot ≡ 1000M_ \ odot / m_p $$

Onde, m _p = massa do próton.

Então obtemos aproximadamente a densidade numérica de bárions $ \ Omega b ∼ = 0,025 $. Isso implica $ \ rho b = 0,25% $ de $ \ rho_c $. Pesquisas diferentes produziram um valor ligeiramente diferente. Portanto, no universo local, a densidade numérica da matéria visível é muito menor do que a densidade crítica, o que significa que estamos vivendo em um universo aberto.

A massa com um fator de 10 não está incluída nessas pesquisas porque elas levam em consideração a radiação eletromagnética, mas não a matéria escura. Doando, $ \ Omega_m = 0,3 - 0,4 $. Ainda conclui que vivemos em um universo aberto.

A matéria escura interage com a gravidade. Muita matéria escura pode interromper a expansão. Ainda não formalizamos como $ \ rho $ muda com o tempo, para o qual precisamos de outro conjunto de equações.

A termodinâmica afirma que -

$$ dQ = dU + dW $$

Para um sistema que cresce em termos de tamanho, $ dW = P dV $. A expansão do universo é modelada como adiabática, ou seja, $ dQ = 0 $. Portanto, a mudança de volume deve acontecer a partir da mudança na energia interna dU.

Tomemos um certo volume do universo de raio de movimentação unitário, ou seja, $ r_c = 1 $. Se $ \ rho $ é a densidade do material dentro deste volume de espaço, então,

$$ M = \ frac {4} {3} \ pi a ^ 3r_c ^ 3 \ rho $$

$$ U = \ frac {4} {3} \ pi a ^ 3 \ rho c ^ 2 $$

Onde, Ué a densidade de energia. Vamos descobrir a mudança na energia interna com o tempo, conforme o universo se expande.

$$ \ frac {\ mathrm {d} U} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ rho c ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} + \ frac {4} {3} \ pi a ^ 3 c ^ 2 \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t} $$

Da mesma forma, a mudança no volume com o tempo é dada por,

$$ \ frac {\ mathrm {d} V} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

Substituindo $ dU = −P dV $. Nós temos,

$$ 4 \ pi a ^ 2 (c ^ 2 \ rho + P) \ ponto {a} + \ frac {4} {3} \ pi a ^ 3c ^ 2 \ dot {\ rho} = 0 $$

$$ \ dot {\ rho} +3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Isso é chamado de Fluid Equation. Diz-nos como a densidade do universo muda com o tempo.

A pressão cai conforme o universo se expande. A cada instante a pressão muda, mas não há diferença de pressão entre dois pontos no volume considerado, portanto, o gradiente de pressão é zero. Apenas materiais relativísticos transmitem pressão, a matéria é sem pressão.

A Equação de Friedmann, juntamente com a Equação de Fluido, modela o universo.

Pontos para lembrar

• A matéria escura interage com a gravidade. Muita matéria escura pode interromper a expansão.

• A equação do fluido nos diz como a densidade do universo muda com o tempo.

• A Equação de Friedmann, juntamente com a Equação de Fluido, modela o universo.

• Apenas materiais relativísticos transmitem pressão, a matéria é sem pressão.

Neste capítulo, discutiremos as soluções para as equações de Friedmann relativas ao universo dominado pela matéria. Na cosmologia, porque estamos vendo tudo em grande escala, os sistemas solares, as galáxias, tudo passa a ser como partículas de poeira (é o que vemos com os nossos olhos), podemos chamar de universo empoeirado ou universo só de matéria.

No Fluid Equation,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho -3 \ left (\ frac {\ dot {a}} {a} \ right ) \ left (\ frac {P} {c ^ 2} \ right) $$

Podemos ver que existe um termo de pressão. Para um universo empoeirado,P = 0, porque a densidade de energia da matéria será maior do que a pressão da radiação, e a matéria não está se movendo com velocidade relativística.

Então, a Equação do Fluido se tornará,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho $$

$$ \ Rightarrow \ dot {\ rho} a + 3 \ dot {a} \ rho = 0 $$

$$ \ Rightarrow \ frac {1} {a ^ 3} \ frac {\ mathrm {d}} {\ mathrm {d} t} (a ^ 3 \ rho) = 0 $$

$$ \ Rightarrow \ rho a ^ 3 = \: constante $$

$$ \ Rightarrow \ rho \ propto \ frac {1} {a ^ 3} $$

Não há contra-intuição nesta equação porque a densidade deve escalar como $ a ^ {- 3} $ porque o volume está aumentando como $ a ^ 3 $.

Da última relação, podemos dizer que,

$$ \ frac {\ rho (t)} {\ rho_0} = \ left [\ frac {a_0} {a (t)} \ right] ^ 3 $$

Para o universo atual, a, que é igual a a₀ deve ser 1. Então,

$$ \ rho (t) = \ frac {\ rho_0} {a ^ 3} $$

Em um universo plano dominado pela matéria, k = 0. Assim, a equação de Friedmann se tornará,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ dot {a} ^ 2 = \ frac {8 \ pi G \ rho a ^ 2} {3} $$

Ao resolver esta equação, obteremos,

$$ a \ propto t ^ {2/3} $$

$$ \ frac {a (t)} {a_0} = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Isso significa que o universo continuará aumentando com uma taxa decrescente. A imagem a seguir mostra a expansão de um Universo empoeirado.

Como ρ muda com o tempo?

Dê uma olhada na seguinte equação -

$$ \ frac {\ rho (t)} {\ rho_0} = \ left (\ frac {t_0} {t} \ right) ^ 2 $$

Sabemos que o fator de escala muda com o tempo como $ t ^ {2/3} $. Então,

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Diferenciando-o, teremos,

$$ \ frac {(da)} {dt} = \ ponto {a} = \ frac {2} {3} \ left (\ frac {t ^ {- 1/3}} {t_0} \ right) $$

Nós sabemos que o Hubble Constant é,

$$ H (t) = \ frac {\ dot {a}} {a} = \ frac {2} {3t} $$

Esta é a equação para Einstein-de sitter Universe. Se quisermos calcular a idade atual do universo, então,

$$ t_0 = t_ {idade} = \ frac {2} {3H_0} $$

Depois de colocar o valor de $ H_0 $ para o universo presente, obteremos o valor da idade do universo como 9 Gyrs. Há muitosGlobular Cluster em nossa própria galáxia, a Via Láctea, que tem idades mais do que isso.

Era tudo sobre o universo empoeirado. Agora, se você assumir que o universo é dominado pela radiação e não pela matéria, a densidade de energia da radiação será $ a ^ {- 4} $ em vez de $ a ^ {- 3} $. Veremos mais disso no próximo capítulo.

Pontos para lembrar

• Na cosmologia, tudo passa a ser como partículas de poeira, portanto, nós o chamamos de universo empoeirado ou universo somente matéria.

• Se assumirmos que o universo é dominado pela radiação e não pela matéria, então a densidade de energia da radiação será $ a ^ {- 4} $ em vez de $ a ^ {- 3} $.

Neste capítulo, discutiremos as soluções para as equações de Friedmann relacionadas ao universo dominado por radiação. No início, comparamos a densidade de energia da matéria com a da radiação. Isso nos permitirá ver se nosso universo é dominado pela matéria ou pela radiação.

Densidade de energia da radiação

A radiação predominante no universo atual pode ser atribuída muito pouco às fontes estelares, mas é principalmente devido ao CMB (Fundo Cósmico de Microondas) remanescente.

A densidade de energia da radiação, $ \ epsilon _ {\ gamma, 0} $, pode ser expressa da seguinte forma -

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$

Aqui, a é a constante de radiação que tem a expressão $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ igual a a = 7.5657 × 10⁻¹⁵erg\: cm⁻³ K⁻⁴. A Temperatura, T0, que consideramos aqui, corresponde à do corpo negro correspondente à CMB.

Substituindo os resultados, temos,

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ vezes 10 ^ {- 13} erg \: cm ^ {- 3} $$

Densidade de energia da matéria

Nos cálculos a seguir, temos a suposição de trabalhar com um universo plano e K = 0. Consideramos a densidade de energia da matéria como $ \ epsilon = \ rho c ^ 2 $. Nós consideramos o seguinte -

$$ \ rho_ {m, 0} c ^ 2 = 0,3 \ rho_ {c, 0} c ^ 2 = 0,3 \ vezes \ frac {3H_0 ^ 2} {8 \ pi G} \ vezes c ^ 2 $$

$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ vezes 10 ^ {- 8} erg \: cm ^ {- 3} $$

$$ \ rho_ {b, 0} c ^ 2 = 0,03 \ rho_ {c, 0} c ^ 2 = 0,03 \ vezes \ frac {3H_0 ^ 2} {8 \ pi G} \ vezes c ^ 2 $$

$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ vezes 10 ^ {- 9} erg \: cm ^ {- 3} $$

Assim, a partir do cálculo acima, vemos que vivemos em um universo dominado pela matéria. Isso pode ser comprovado pelo fato de que o CMB é muito frio. Ao olharmos para trás no tempo, teríamos a temperatura CMB ficando mais quente, e seremos capazes de concluir que pode ter havido uma época em que o universo era dominado pela radiação.

Variação de densidade e fator de escala

A equação do fluido nos mostra que -

$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Se considerarmos um universo empoeirado, teríamos P = 0. Deixando de lado os resultados anteriores, consideramos o universo como dominado pela radiação.

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$

Usando a relação de pressão de $ P_ {rad} = \ rho c ^ {2/3} $ temos -

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$

$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$

Para simplificar ainda mais, temos,

$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$

$$ \ rho_ {rad} a ^ 4 = \: constante $$

$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$

O resultado acima mostra uma ^4ª variação de potência inversa de a com $ \ rho $.

Isso pode ser interpretado fisicamente como $ a ^ {- 3} $ vindo da variação no volume à medida que aumenta. O restante $ a ^ {- 1} $ pode ser tratado como a energia perdida pelo fóton devido à expansão do espaço no universo (redshift cosmológico 1 + z = a ^-1 ).

A imagem a seguir mostra a variação da densidade da matéria e da radiação com o tempo.

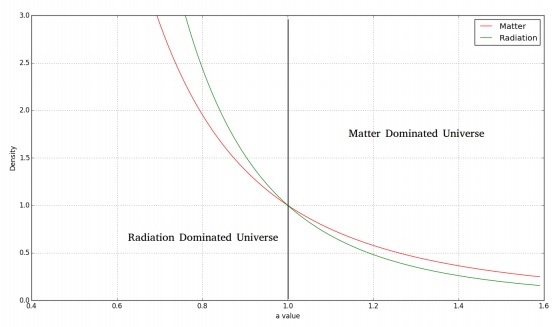
Para um universo plano, dominado por radiação, teríamos a equação de Friedmann da seguinte forma -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$

Na simplificação e aplicação da solução à equação diferencial, temos -

$$ (\ ponto {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$

$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$

Assim, temos -

$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$

Pela equação acima, vemos que a taxa de aumento do fator de escala é menor do que a do universo empoeirado.

Pontos para lembrar

• A radiação predominante no universo atual pode ser atribuída muito pouco às fontes estelares.

• Para um universo empoeirado, a pressão é zero.

• CMB está muito frio.

A área de Energia Escura é uma área muito cinza na astronomia porque é um parâmetro livre em todas as equações, mas não há uma ideia clara do que exatamente é.

Começaremos com as equações de Friedmann,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} $$

A maioria dos livros elementares sobre cosmologia, todos eles começam com a descrição da energia escura deste episódio que antes da observação de Hubble, o universo é fechado e estático.

Agora, para o universo ser estático no lado direito, ambos os termos devem corresponder e devem ser zero, mas se o primeiro termo for maior que o segundo termo, então o universo não será estático, então Einstein abandonou o parâmetro livre ∧ na equação de campo para tornar o universo estático, então ele argumentou que não importa o que o primeiro termo é comparado ao segundo termo, você sempre pode obter um universo estático se houver mais um componente na equação, que pode compensar a dis- correspondência entre esses dois termos.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

$$ \ left (\ frac {\ ddot {a}} {a} \ right) = - \ frac {4 \ pi G} {3} \ left (\ rho + \ frac {3P} {c ^ 2} \ direita) + \ frac {\ wedge} {3} $$

Onde $ P = \ rho \ ast c ^ 2/3 $ e $ \ wedge = \ rho \ ast c ^ 2 $ é o Parâmetro Cosmológico. (O sinal negativo é apenas por causa da atração)

Na equação acima (equação de aceleração) -

• $ 3P / c ^ 2 $ é a pressão negativa devido à radiação,

• $ -4 \ pi G / 3 $ é a atração devido à gravidade, e

• $ \ wedge / 3 $ faz uma contribuição positiva.

O terceiro termo atua como uma força repulsiva porque outra parte da equação é atrativa.

O significado físico da equação é que ˙a = 0porque não havia nenhuma evidência que mostrasse que o universo está se expandindo. E se esses dois termos não corresponderem um ao outro, então é melhor adicionar um componente e dependendo do deslocamento, sempre podemos alterar o valor do parâmetro livre.

Naquela época não havia explicação física sobre esses parâmetros cosmológicos, por isso quando a explicação do universo em expansão foi descoberta na década de 1920, onde Einstein imediatamente teve que jogar fora esta constante.

A explicação disso cosmological constant ainda está em uso porque explica uma versão diferente do universo, mas a definição dessa constante cosmológica, a forma de interpretação, mudou com o tempo.

Agora, o conceito dessa constante cosmológica foi trazido de volta à cosmologia por muitas razões. Uma das razões é que temos observações para densidade de energia de diferentes componentes do universo (bariônico, matéria escura, radiação), então sabemos qual é esse parâmetro. Observações independentes usandocosmic microwave background mostra que k = 0.

$$ CMB, k = 0 \: \ rho = \ rho_c = \ frac {3H_0 ^ 2} {8 \ pi G} \ approx 10 \: Hidrogênio \: átomos.m ^ {- 3} $$

Para k ser 0, $ \ rho $ deve ser igual a $ \ rho_c $, mas tudo o que sabemos se somarmos isso não resulta em 0, o que significa que há algum outro componente que mostra que é muito menor que $ \ rho_c $.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ {rad} << \ rho_c $$

Mais uma evidência da energia escura vem do Type 1 Supernova Observationque ocorre quando a anã branca acrescenta a matéria e excede o limite de Chandrashekhar, que é um limite muito preciso (≈ 1,4M). Agora, toda vez que ocorre uma explosão de supernova tipo 1, temos a mesma massa, o que significa que a energia de ligação total do sistema é a mesma e a quantidade de energia de luz que podemos ver é a mesma.

É claro que a luz da supernova aumenta e depois desmaia, mas se você medir o brilho máximo, ele sempre será o mesmo, o que o torna um candidato padrão. Assim, com uma Supernova Tipo 1, usamos para medir o componente cosmológico do universo e os astrônomos descobriram que a supernova com alto desvio para o vermelho é 30% - 40% mais fraca do que a supernova com baixo desvio para o vermelho e pode ser explicado se houver -zero∧ prazo.

Em modelos cosmológicos DE (Dark Energy)é tratado como um fluido, o que significa que podemos escrever a equação de estado para ele. A equação de estado é a equação que conecta as variáveis ​​como pressão, densidade, temperatura e volume de dois estados diferentes da matéria.

Dimensionalmente, vemos,

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {\ wedge} {3} $$

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} $$

Densidade de energia de DE,

$$ \ epsilon_ \ wedge = \ rho_ \ wedge \ ast c ^ 2 = \ frac {\ wedge c ^ 2} {8 \ pi G} $$

Parâmetro de densidade de energia escura,

$$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $$

$ \ Omega_ \ wedge $ é a densidade da energia escura em termos de densidade crítica.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ \ wedge $$

Existem várias teorias sobre a energia escura, que está repelindo o universo e fazendo com que ele se expanda. Uma hipótese é que essa energia escura poderia ser uma densidade de energia do vácuo. Suponha que o próprio espaço esteja processando alguma energia e quando você conta a quantidade de matéria bariônica, matéria escura e a radiação dentro do volume unitário do espaço, você também está contando a quantidade de energia que está associada ao espaço, mas não está claro que a energia escura é realmente uma densidade de energia do vácuo.

Sabemos que a relação entre densidade e fator de escala para matéria escura e radiação são,

$$ \ rho_m \ propto \ frac {1} {a ^ 3} $$

$$ \ rho_m \ propto \ frac {1} {a ^ 4} $$

Temos o gráfico do fator de escala de densidade v / s. No mesmo gráfico, podemos ver que $ \ rho_ \ wedge $ é uma constante com a expansão do universo que não depende do fator de escala.

A imagem a seguir mostra a relação entre a densidade e o fator de escala.

‘ρ’ v/s ‘a’(fator de escala relacionado ao tempo) no mesmo gráfico, a energia escura é modelada como uma constante. Portanto, qualquer que seja a energia escura que medimos no universo atual, é uma constante.

Pontos para lembrar

• Observações independentes usando radiação cósmica de fundo mostram que k = 0.

• $ \ rho_ \ wedge $ é uma constante com a expansão do universo que não depende do fator de escala.

• A gravidade também está mudando com o tempo, o que é chamado modified Newtonian dynamics.

Neste capítulo, discutiremos as curvas de rotação da galáxia espiral e as evidências de matéria escura.

Matéria escura e fato observacional sobre a matéria escura

• A evidência inicial da matéria escura foi a study of the Kinematics of Spiral Galaxy.

• O Sol está deslocado 30.000 anos-luz do centro de nossa galáxia. A velocidade central da galáxia é de 220 km / s.

• Por que a velocidade de 220 km / s não é 100 km / s ou 500 km / s? O que governa o movimento circular do objeto?

• A massa contida no raio ajuda a detectar a velocidade no Universo.

Rotação da Via Láctea ou Galáxia Espiral - Rotação Diferencial

• Angular Velocity varia com a distância do centro.

• O período orbital depende da distância do centro.

• O material mais próximo do Centro Galáctico tem um período de tempo mais curto e o material longe do Centro Galáctico tem um período de tempo maior.

Curva de Rotação

• Preveja a mudança de velocidade com o Galactic centric radius. A curva que fornece as mudanças de velocidade com o raio orbital.

• Quando vemos as coisas se movendo, pensamos que é a gravidade que influencia a rotação.

• A distribuição da massa varia com o raio. A densidade da matéria irá prever a curva de rotação. A curva de rotação com base na densidade da matéria, que varia com o raio.

Brilho da superfície

• Nós escolhemos o patch e vemos quanta luz está saindo.

• A quantidade de luz proveniente do patch é chamada de brilho da superfície.

• Sua unidade é mag/arcsec².

• Se descobrirmos que o brilho da superfície varia com o raio, podemos descobrir que a matéria luminosa varia com o raio.

  $$ \ mu (r) \ propto exp \ left (\ frac {-r} {h_R} \ right) $$

  $ h_R $ é o comprimento da escala. $ \ mu (r) = \ mu_o \ ast exp \ left (\ frac {-r} {h_R} \ right) $

• $ h_R $ é quase 3 kpc para a Via Láctea.

Galáxias Espirais

Para que os astrônomos entendam a curva rotacional, eles dividem as galáxias em dois componentes, que são -

• Disk
• Bulge

A imagem a seguir mostra uma protuberância esférica central + disco circular. A distribuição estelar e de gás é diferente na protuberância e no disco.

Cinemática de Galáxias Espirais

• A velocidade circular de qualquer objeto - para a protuberância é (r <Rb).

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

  $$ M (r) = \ frac {4 \ pi r ^ 3} {3} \ ast \ rho_b $$

• Para o disco - (Rb <r <Rd)

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

• Bulge tem uma densidade aproximadamente constante de estrelas.

• A densidade dentro da saliência é constante (não muda com a distância dentro da saliência).

• Em um disco, a densidade estelar diminui com o raio. O raio aumenta e a matéria luminosa diminui.

• A granel - $ V (r) \ propto r $

• No disco - $ V (r) \ propto 1 / \ sqrt {r} $

Curva Rotacional de Galáxias Espirais

• Através de Spectroscopy (galáxias próximas - resolvida espacialmente a galáxia), produzimos a curva de rotação.

• Como mencionado acima, vemos que a curva de rotação é plana nas regiões externas, ou seja, as coisas estão se movendo rapidamente nas regiões externas, o que geralmente não é esperado nesta forma.

• A velocidade orbital aumenta com o aumento do raio da região interna, mas fica achatada na região externa.

Matéria escura

Diz-se que a matéria escura é o componente não luminoso do universo. Vamos entender sobre a matéria escura através das seguintes dicas.

• As curvas de rotação planas são contrárias ao que vemos para a distribuição de estrelas e gás nas galáxias espirais.

• A luminosidade da superfície do disco cai exponencialmente com o raio, implicando que a massa da matéria luminosa, principalmente estrelas, está concentrada em torno do centro galáctico.

• O achatamento da curva de rotação sugere que a massa total da galáxia dentro de algum raio r está aumentando sempre com o aumento de r.

• Isso só pode ser explicado se houver uma grande quantidade de massa gravitante invisível nessas galáxias que não esteja emitindo radiação eletromagnética.

• As medições da curva de rotação de galáxias espirais é um dos conjuntos de evidências mais convincentes para a matéria escura.

Evidência de matéria escura

• Missing Mass - 10 vezes a massa luminosa.

• A maior parte dessa matéria escura deve estar no halo da galáxia: grandes quantidades de matéria escura no disco podem perturbar a estabilidade de longo prazo do disco contra as forças das marés.

• Uma pequena fração da matéria escura no disco pode ser bariônica - estrelas escuras (anãs marrons, anãs negras) e remanescentes estelares compactos (estrelas de nêutrons, buracos negros). Mas essa matéria escura bariônica não pode explicar a escala completa da massa ausente nas galáxias.

• Perfil de densidade da matéria escura - $ M (r) \ propto r $ e $ \ rho (r) \ propto r ^ {- 2} $.

• Os dados da curva de rotação para galáxias espirais são consistentes com a matéria escura distribuída em seu halo.

• Este halo escuro constitui grande parte da massa total da galáxia.

• Toda a matéria bariônica (estrelas, aglomerados de estrelas, ISM, etc.) é mantida unida pelo potencial gravitacional deste halo de matéria escura.

Conclusão

• A matéria escura só foi detectada por meio de sua interação gravitacional com uma matéria comum. Nenhuma interação com a luz (nenhuma força eletromagnética) ainda foi observada.

• Neutrinos- Carregue menos, interagindo fracamente, mas a massa é muito menor (<0,23 eV). Partículas de DM devem ter E> 10 eV ou mais para explicar a formação da estrutura.

• Partículas maciças de interação fraca (WIMPS) podem ser a fonte de matéria escura.

Pontos para lembrar

• O material mais próximo do centro galáctico tem um período de tempo mais curto.

• Bulge tem uma densidade aproximadamente constante de estrelas.

• A luminosidade da superfície do disco diminui exponencialmente com o raio.

• Grandes quantidades de matéria escura no disco podem perturbar a estabilidade a longo prazo do disco contra as forças das marés.

A primeira evidência direta de matéria escura veio de Frids Ricky. Ele fez algumas observações que revelaram matéria escura pela primeira vez. Suas observações consideraram o movimento geral dentro do aglomerado de galáxias.

Objetos estendidos são aglomerados de galáxias e são considerados estruturas limitadas. Essas galáxias estão se movendo em relação ao centro do aglomerado, mas não voam. Observamos o movimento geral da galáxia.

Premissa: as velocidades são representativas do potencial subjacente

Cada galáxia terá seu próprio movimento dentro do aglomerado e Hubble Flow Component. As galáxias menores são menores, a maior parte da luz vem de M31 e MW, existem várias galáxias anãs. Para nossa análise bruta, só podemos usar M31 e MW e avaliar a massa dinâmica do grupo local.

Existe uma velocidade relativa entre nós e M31. É grosseiro, mas é verdade. A história começa muito tempo atrás, quando M31 e MW estavam próximos um do outro, porque eram membros de um cluster que estavam se afastando um do outro. Depois de algum tempo, eles alcançam a separação máxima e, em seguida, se aproximam.

Digamos que a separação máxima que pode atingir seja $ r_ {max} $. Agora eles têm uma separação chamadar. DeixeiMser a massa combinada de MW e M31. Não sabemos quando $ r_ {max} $ é atingido.

$$ \ frac {GM} {r_ {max}} = \: Potencial \: em \: r_ {max} $$

Quando essas galáxias estavam se aproximando umas das outras em algum instante r, então a energia do sistema será -

$$ \ frac {1} {2} \ sigma ^ 2 = \ frac {GM} {r} = \ frac {GM} {r_ {max}} $$

σ é a velocidade relativa de ambas as galáxias. M é a massa reduzida apenas, mas a massa de teste é 1. σ é a velocidade de qualquer objeto à distância rdo centro do cluster. Acreditamos que este cluster está em equação dinâmica porque o teorema virial é válido. Portanto, as galáxias não podem vir com velocidades diferentes.

Quanto tempo essas galáxias levariam para atingir a distância máxima?

Para entender isso, consideremos a seguinte equação.

$$ \ frac {1} {2} \ left (\ frac {dr} {dt} \ right) ^ 2 = \ frac {GM} {r} - \ frac {GM} {r_ {max}} $$

$$ t_ {max} = \ int_ {0} ^ {r_ {max}} dt = \ int_ {0} ^ {r_ {max}} \ frac {dr} {\ sqrt {2GM}} \ left (\ frac {1} {r} - \ frac {1} {r_ {max}} \ right) ^ 2 $$

$$ t_ {max} = \ frac {\ pi r_ {max} ^ {\ frac {3} {2}}} {2 \ sqrt {2GM}} $$

Onde, M = massa dinâmica do grupo local. O tempo total desde o início até o final da colisão é $ 2t_ {max} $. Portanto,

$$ 2t_ {max} = t_0 + \ frac {D} {\ sigma} $$

E $ t_0 $ é a idade atual do universo.

Se $ t_ {max} real <RHS $, então temos um limite inferior para o tempo. $ D / \ sigma $ é o momento em que eles colidirão novamente. Aqui, assumimos que σ é constante.

$$ t_ {max} = \ frac {t_0} {2} + \ frac {D} {2 \ sigma} $$

$$ r_ {max} = t_ {max} \ times \ sigma = 770K_ {pc} $$

Aqui, σ = velocidade relativa entre MW e M31.

$$ M_ {dynamic} = 3 \ vezes 10 ^ {12} M_0 $$

$$ M_ {MW} ^ {lum} = 3 \ vezes 10 ^ {10} M_0 $$

$$ M_ {M31} ^ {lum} = 3 \ vezes 10 ^ {10} M_0 $$

Mas, na prática, a massa dinâmica é descoberta considerando cada galáxia dentro do aglomerado. A massa que falta é a matéria escura eFrids Rickynotou que as galáxias no aglomerado de coma estão se movendo muito rápido. Ele previu a existência de estrelas de nêutrons um ano após a descoberta das estrelas de nêutrons e usou o telescópio Palomar para encontrar a supernova.

Pontos para lembrar

• A primeira evidência direta de matéria escura veio de Frids Ricky.

• Objetos estendidos são aglomerados de galáxias e são considerados bound structures.

• Dynamic mass é descoberto considerando cada galáxia dentro do aglomerado.

Neste capítulo, discutiremos sobre os parâmetros de densidade e Hubble.

Parâmetro Hubble

O parâmetro Hubble é definido da seguinte forma -

$$ H (t) \ equiv \ frac {da / dt} {a} $$

que mede a rapidez com que o fator de escala muda. De maneira mais geral, a evolução do fator de escala é determinada pela Equação de Friedmann.

$$ H ^ 2 (t) \ equiv \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

Onde, ∧ é uma constante cosmológica.

Para um universo plano, k = 0, portanto, a Equação de Friedmann torna-se -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {\ wedge} {3} $$

Para um universo dominado por matéria, a densidade varia como -

$$ \ frac {\ rho_m} {\ rho_ {m, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 3 \ Rightarrow \ rho_m = \ rho_ {m, 0} a ^ {- 3} $$

e, para um universo dominado por radiação, a densidade varia como -

$$ \ frac {\ rho_ {rad}} {\ rho_ {rad, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 4 \ Rightarrow \ rho_ {rad} = \ rho_ {rad, 0} a ^ {- 4} $$

Atualmente, vivemos em um universo dominado pela matéria. Portanto, considerando $ \ rho ≡ \ rho_m $, obtemos -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {\ wedge} {3} $$

A constante cosmológica e a densidade de energia escura estão relacionadas da seguinte forma -

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} \ Rightarrow \ wedge = 8 \ pi G \ rho_ \ wedge $$

A partir disso, obtemos -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {8 \ pi G} {3} \ rho_ \ wedge $$

Além disso, a densidade crítica e a constante de Hubble estão relacionadas da seguinte forma -

$$ \ rho_ {c, 0} = \ frac {3H_0 ^ 2} {8 \ pi G} \ Rightarrow \ frac {8 \ pi G} {3} = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} $$

A partir disso, obtemos -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ {m, 0} a ^ {- 3} + \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ \ wedge $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 3} + H_0 ^ 2 \ Omega _ {\ wedge, 0 } $$

$$ (\ dot {a}) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 1} + H_0 ^ 2 \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} \ frac {1} {a} + \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) + \ Omega _ {\ wedge, 0} \ frac {1} { (1 + z) ^ 2} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 (1 + z) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge , 0} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 \ frac {1} {a ^ 2} = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {\ wedge, 0} $$

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge, 0} $$

Aqui, $ H (z) $ é o parâmetro Hubble dependente do deslocamento para o vermelho. Isso pode ser modificado para incluir o parâmetro de densidade de radiação $ \ Omega_ {rad} $ e o parâmetro de densidade de curvatura $ \ Omega_k $. A equação modificada é -

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4+ \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

$$ Ou, \: \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = E (z) $$

$$ Ou, \: H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

Onde,

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

Isso mostra que o parâmetro Hubble varia com o tempo.

Para o Einstein-de Sitter Universo, $ \ Omega_m = 1, \ Omega_ \ wedge = 0, k = 0 $.

Colocando esses valores, obtemos -

$$ H (z) = H_0 (1 + z) ^ {\ frac {3} {2}} $$

que mostra a evolução temporal do parâmetro Hubble para o universo de Einstein-de Sitter.

Parâmetro de Densidade

O parâmetro de densidade, $ \ Omega $, é definido como a razão entre a densidade real (ou observada) ρ e a densidade crítica $ \ rho_c $. Para qualquer quantidade $ x $, o parâmetro de densidade correspondente, $ \ Omega_x $ pode ser expresso matematicamente como -

$$ \ Omega_x = \ frac {\ rho_x} {\ rho_c} $$

Para diferentes quantidades em consideração, podemos definir os seguintes parâmetros de densidade.

S.No.	Quantidade	Parâmetro de Densidade
1	Bárions	$ \ Omega_b = \ frac {\ rho_b} {\ rho_c} $
2	Matéria (bariônico + escuro)	$ \ Omega_m = \ frac {\ rho_m} {\ rho_c} $
3	Energia escura	$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $
4	Radiação	$ \ Omega_ {rad} = \ frac {\ rho_ {rad}} {\ rho_c} $

Onde os símbolos têm seus significados usuais.

Pontos para lembrar

• A evolução do fator de escala é determinada pelo Friedmann Equation.

• H(z) é o parâmetro Hubble dependente do deslocamento para o vermelho.

• o Hubble Parameter varia com o tempo.

• o Density Parameter é definido como a razão entre a densidade real (ou observada) e a densidade crítica.

Conforme discutido nos capítulos anteriores, a evolução do tempo do parâmetro Hubble é dada por -

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

Onde z é o desvio para o vermelho e E(Z) é -

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega ^ {\ wedge, 0} $$

Se a expansão do universo for constante, a verdadeira idade do universo é dada da seguinte forma -

$$ t_H = \ frac {1} {H_0} $$

Se for o universo dominado pela matéria, ou seja, o universo de Einstein Desitter, então a verdadeira idade do universo é dada por -

$$ t_H = \ frac {2} {3H_0} $$

A escala e o Redshift são definidos por -

$$ a = \ frac {a_0} {1 + z} $$

A idade do universo em termos do parâmetro cosmológico é derivada da seguinte forma.

O parâmetro Hubble é dado por -

$$ H = \ frac {\ frac {da} {dt}} {a} $$

Diferenciando, temos -

$$ da = \ frac {-dz} {(1 + z) ^ 2} $$

Onde a₀ = 1 (valor presente do fator de escala)

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {-1} {(1 + z) ^ 2} $$

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} { \ mathrm {d} t} $$

$$ H = \ frac {\ dot {a}} {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} {\ mathrm {d } t} \ frac {1 + z} {1} $$

$$ \ frac {\ dot {a}} {a} = \ frac {-1} {1 + z} \ frac {\ mathrm {d} z} {\ mathrm {d} t} \ frac {1} { 1} $$

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

$$ dt = \ frac {-dz} {H_0E (z) ^ {\ frac {1} {2}} (1 + z)} $$

Se quisermos encontrar a idade do universo em qualquer desvio para o vermelho ‘z’ então -

$$ t (z) = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac {1} {2}} (1+ z)} dz $$

Onde k é o parâmetro de densidade de curvatura e -

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

Para calcular a idade atual do universo, tome z₁ = 0.

$$ t (z = 0) = t_ {idade} = t_0 = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac { 1} {2}} (1 + z)} dz $$

Para o Modelo Desitter de Einstein, ou seja, $ \ Omega_m = 1 $, $ \ Omega_ {rad} = 0 $, $ \ Omega_k = 0 $, $ \ Omega_ \ wedge = 0 $, a equação para a idade do universo torna-se -

$$ t_ {idade} = \ frac {1} {H_0} \ int_ {0} ^ {\ infty} \ frac {1} {(1 + z) ^ {\ frac {5} {2}}} dz $ $

Depois de resolver a integral, obtemos -

$$ t_H = \ frac {2} {3H_0} $$

O céu noturno é como um Cosmic Time Machine.Sempre que observamos um planeta, estrela ou galáxia distante, estamos vendo-o como era há horas, séculos ou mesmo milênios. Isso ocorre porque a luz viaja a uma velocidade finita (a velocidade da luz) e dadas as grandes distâncias no Universo, não vemos os objetos como eles são agora, mas como eram quando a luz foi emitida. O tempo decorrido entre - quando detectamos a luz aqui na Terra e quando ela foi originalmente emitida pela fonte, é conhecido comoLookback Time (t_L(z₁)).

Portanto, o tempo de lookback é dado por -

$$ t_1 (z_1) = t_0-t (z_1) $$

O tempo de retrospectiva para o Universo de Einstein Desitter é -

$$ t_L (z) = \ frac {2} {3H_0} \ left [1- \ frac {1} {(1 + z) ^ {\ frac {3} {2}}} \ right] $$

Pontos para lembrar

• Sempre que observamos um planeta, estrela ou galáxia distante, estamos vendo-o como era há horas, séculos ou mesmo milênios.

• O tempo decorrido entre - quando detectamos a luz aqui na Terra e quando ela foi originalmente emitida pela fonte, é conhecido como tempo de lookback.

Neste capítulo, vamos entender o que é a Distância do Diâmetro Angular e como ela ajuda na Cosmologia.

Para o universo presente -

• $ \ Omega_ {m, 0} \: = \: 0,3 $

• $ \ Omega _ {\ wedge, 0} \: = \: 0,69 $

• $ \ Omega_ {rad, 0} \: = \: 0,01 $

• $ \ Omega_ {k, 0} \: = \: 0 $

Estudamos dois tipos de distâncias até agora -

• Proper distance (lp) - A distância que os fótons viajam da fonte até nós, ou seja, o Instantaneous distance.

• Comoving distance (lc) - Distância entre objetos em um espaço que não se expande, ou seja, distance in a comoving frame of reference.

Distância como uma função do Redshift

Considere uma galáxia que irradia um fóton por vez t₁ que é detectado pelo observador em t₀. Podemos escrever a distância adequada para a galáxia como -

$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$

Deixe o redshift da galáxia ser z,

$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$

$$ \ portanto \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$

Agora, comovendo a distância da galáxia a qualquer momento t será -

$$ l_c = \ frac {l_p} {a (t)} $$

$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$

Em termos de z,

$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$

Existem duas maneiras de encontrar distâncias, que são as seguintes -

Relação Fluxo-Luminosidade

$$ F = \ frac {L} {4 \ pi d ^ 2} $$

Onde d é a distância na fonte.

A distância do diâmetro angular de uma fonte

Se soubermos o tamanho de uma fonte, sua largura angular nos dirá sua distância do observador.

$$ \ theta = \ frac {D} {l} $$

Onde l é a distância do diâmetro angular da fonte.

• θ é o tamanho angular da fonte.

• D é o tamanho da fonte.

Considere uma galáxia de tamanho D e tamanho angular dθ.

Nós sabemos isso,

$$ d \ theta = \ frac {D} {d_A} $$

$$ \ portanto D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ porque dr ^ 2 = 0; \: d \ phi ^ 2 \ approx 0 $$

$$ \ Rightarrow D = a (t) rd \ theta $$

Mudando r para r_c, a distância móvel da galáxia, temos -

$$ d \ theta = \ frac {D} {r_ca (t)} $$

Aqui, se escolhermos t = t₀, acabamos medindo a distância atual até a galáxia. MasDé medido no momento da emissão do fóton. Portanto, usandot = t₀, obtemos uma distância maior da galáxia e, portanto, uma subestimação de seu tamanho. Portanto, devemos usar o tempot₁.

$$ \ portanto d \ theta = \ frac {D} {r_ca (t_1)} $$

Comparando isso com o resultado anterior, obtemos -

$$ d_ \ wedge = a (t_1) r_c $$

$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ porque 1 + z_1 = \ frac {1} {a (t_1)} $$

Portanto,

$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$

d_A é a distância do diâmetro angular para o objeto.

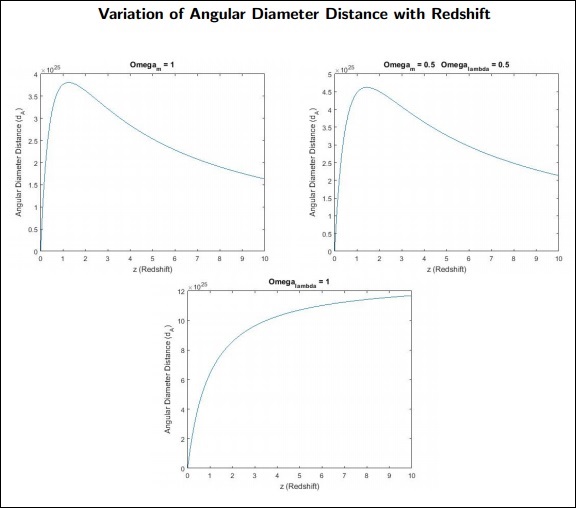
Pontos para lembrar

• Se soubermos o tamanho de uma fonte, sua largura angular nos dirá sua distância do observador.

• Distância adequada é a distância que os fótons viajam da fonte até nós.

• Distância comovente é a distância entre objetos em um espaço que não se expande.

Conforme discutido no capítulo anterior, a distância do diâmetro angular a uma fonte no desvio para o vermelho z é dado por -

$$ d_ \ wedge (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $ $

$$ d_ \ wedge (z_ {gal}) = \ frac {r_c} {1 + z_ {gal}} $$

onde $ r_c $ é a distância móvel.

A distância de luminosidade depende da cosmologia e é definida como a distância na qual o fluxo observado f é de um objeto.

Se a luminosidade intrínseca $ d_L $ de um objeto distante é conhecida, podemos calcular sua luminosidade medindo o fluxo $ f $ que é determinado por -

$$ d_L (z) = \ sqrt {\ frac {L} {4 \ pi f}} $$

A energia do fóton muda para vermelho.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {emi}} = \ frac {a_0} {a_e} $$

onde $ \ lambda_ {obs}, \ lambda_ {emi} $ são observados e os comprimentos de onda emitidos e $ a_0, a_e $ são fatores de escala correspondentes.

$$ \ frac {\ Delta t_ {obs}} {\ Delta t_ {emi}} = \ frac {a_0} {a_e} $$

onde $ \ Delta_t {obs} $ é observado como o intervalo de tempo do fóton, enquanto $ \ Delta_t {emi} $ é o intervalo de tempo no qual eles são emitidos.

$$ L_ {emi} = \ frac {nhv_ {emi}} {\ Delta t_ {emi}} $$

$$ L_ {obs} = \ frac {nhv_ {obs}} {\ Delta t_ {obs}} $$

$ \ Delta t_ {obs} $ levará mais tempo do que $ \ Delta t_ {emi} $ porque o detector deve receber todos os fótons.

$$ L_ {obs} = L_ {emi} \ left (\ frac {a_0} {a_e} \ right) ^ 2 $$

$$ L_ {obs} <L_ {emi} $$

$$ f_ {obs} = \ frac {L_ {obs}} {4 \ pi d_L ^ 2} $$

Para um universo não em expansão, a distância da luminosidade é igual à distância comovente.

$$ d_L = r_c $$

$$ \ Rightarrow f_ {obs} = \ frac {L_ {obs}} {4 \ pi r_c ^ 2} $$

$$ f_ {obs} = \ frac {L_ {emi}} {4 \ pi r_c ^ 2} \ left (\ frac {a_e} {a_0} \ right) ^ 2 $$

$$ \ Rightarrow d_L = r_c \ left (\ frac {a_0} {a_e} \ right) $$

Estamos encontrando a distância de luminosidade $ d_L $ para calcular a luminosidade do objeto emissor $ L_ {emi} $ -

• Interpretation - Se soubermos o desvio para o vermelho zde qualquer galáxia, podemos descobrir $ d_A $ e a partir disso podemos calcular $ r_c $. Isso é usado para descobrir $ d_L $.

• Se $ d_L! = r_c (a_0 / a_e) $, então não podemos encontrar Lemi de $ f_ {obs} $.

A relação entre a distância da luminosidade $ d_L $ e a distância do diâmetro angular $ d_A.

Nós sabemos disso -

$$ d_A (z_ {gal}) = \ frac {d_L} {1 + z_ {gal}} \ left (\ frac {a_0} {a_e} \ right) $$

$$ d_L = (1 + z_ {gal}) d_A (z_ {gal}) \ left (\ frac {a_0} {a_e} \ right) $$

O fator de escala quando os fótons são emitidos é dado por -

$$ a_e = \ frac {1} {(1 + z_ {gal})} $$

O fator de escala para o universo atual é -

$$ a_0 = 1 $$

$$ d_L = (1 + z_ {gal}) ^ 2d_ \ wedge (z_ {gal}) $$

Qual escolher $ d_L $ ou $ d_A $?

• Para uma galáxia de tamanho conhecido e desvio para o vermelho para calcular seu tamanho, então $ d_A $ é usado.

• Se houver uma galáxia com uma dada magnitude aparente, então para descobrir o quão grande ela é, $ d_L $ é usado.

Example - Se for dado que duas galáxias de igual deslocamento para o vermelho (z = 1) e no plano do céu elas são separadas por 2.3 arc sec então qual é a separação física máxima entre os dois?

Para isso, use $ d_A $ da seguinte forma -

$$ d_A (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $$

onde z = 1 substitui H (z) com base nos parâmetros cosmológicos das galáxias.

Pontos para lembrar

• A distância de luminosidade depende de cosmology.

• Se a luminosidade intrínseca $ d_L $ de um objeto distante é conhecida, podemos calcular sua luminosidade medindo o fluxo f.

• Para um universo não em expansão, a distância de luminosidade é igual à comoving distance.

• A distância de luminosidade é sempre maior que o Angular Diameter Distance.

Para qualquer desvio para o vermelho (z), temos dois valores para a distância -

• Distância do diâmetro angular (d _A )
• Distância de luminosidade (d _L )

Não existe uma definição única de distância “cosmológica” no universo. A escolha da distância depende do propósito e da conveniência da aplicação.

Para testar a tendência prevista de como o tamanho angular de um objeto varia com o redshift, um padrão de medida de tamanho é necessário no céu. Este deve ser um objeto que -

• é muito luminoso, de modo que pode ser detectado em z> 1.

• é muito grande, para que possamos determinar seu tamanho angular.

• não evoluiu morfologicamente ao longo do tempo cosmologicamente significativo (z ∼ 1 corresponde a um tempo retrospectivo de cerca de 7 Gyr).

Alguns objetos (como galáxias cD) satisfazem os dois primeiros critérios. Mas quase todos os objetos evoluem morfologicamente com o tempo. Em geral, objetos astrofísicos (fontes estendidas) tendem a ser intrinsecamente menores no passado porque ainda estão em formação.

Distância de Luminosidade

A distância da luminosidade depende da cosmologia. A dependência da distância de luminosidade na cosmologia torna uma medida útil dos parâmetros cosmológicos.

Os parâmetros cosmológicos podem ser estimados se pudermos encontrar uma vela padrão que não evolui intrinsecamente e existe do universo local para o alto redshift.

Uma vela padrão é aquela que não difere em sua luminosidade de uma fonte para outra. A premissa é que qualquer diferença na luminosidade estimada das velas padrão deve ser devido à cosmologia. Uma dessas velas é a Supernova Tipo Ia.

Supernovas Tipo 1a (SNe)

Estes são o resultado da explosão de uma anã branca após o acréscimo de massa suficiente de sua companheira, uma gigante vermelha ou estrela de sequência principal semelhante, em um sistema binário. Depois que a gigante vermelha chega mais perto do que a distância do lóbulo de Roche da anã branca, a transferência de massa começa e, eventualmente, a anã branca explode liberando uma grande quantidade de energia, não deixando nenhum núcleo para trás. Eles são chamados de Supernovas Tipo 1a. A taxa típica de explosão de Supernovas Tipo 1a em uma galáxia é de 1 por século.

A busca pelo SNe Tipo 1a vem acontecendo com diferentes equipes -

• Equipe de pesquisa de supernova de alto z (Brian Schmidt, Adam Reiss et al.)
• Projeto de Cosmologia Supernova (Saul Perlmutter et al.)

Houve outra equipe de pesquisa chamada Carnegie Supernovae Project que deu resultados semelhantes.

A similaridade dos resultados de diferentes equipes mostra a natureza cosmológica do SNe Tipo 1a. Portanto, eles são velas padrão eficientes.

Pontos para lembrar

• Não existe uma definição única de distância “cosmológica” no universo.

• Distância do diâmetro angular e Distância da luminosidade são as mais usadas.

• Uma vela padrão é aquela que não difere em sua luminosidade de uma fonte para outra.

• Tipo 1a SNe satisfaz os critérios de ser uma vela padrão.

O CMB (Cosmic Microwave Background) é essencialmente constituído pelos fótons da época em que a matéria e a radiação estavam em equilíbrio. Na década de 1920, a ideia de um universo em expansão foi aceita e poderia responder a várias perguntas. Mas as perguntas sobre a abundância de elementos mais pesados ​​e a abundância ficaram sem resposta. Além disso, o universo em expansão implicava que a densidade da matéria deveria diminuir para 0.

Em 1948, George Gammow e Ralph Alpher explicaram a origem dos elementos mais pesados ​​e a abundância usando o “Big Bang”. Eles, juntamente com Robert Herman, previram a existência de “Radiação Relict” ou radiação remanescente do “Big Bang”. A temperatura prevista para esta radiação remanescente foi entre 50-6 K. Em 1965, Robert Dicke, Jim Peebles e David Wilkinson, juntamente com o Grupo de Pesquisa Amo Perizias, detectaram experimentalmente o CMB.

O universo primitivo era muito quente e a energia muito alta para que a matéria permanecesse neutra. Portanto, a matéria estava na forma ionizada -Plasma. A radiação (fótons) e a matéria (plasma) interagiram principalmente por meio dos três processos a seguir.

• Compton Scattering - (Processo de interação principal) Espalhamento inelástico entre fóton de alta energia e partícula carregada de baixa energia.

• Thomson Scattering - Espalhamento elástico de fóton por uma partícula carregada livre.

• Inverse Compton Scattering- Partícula carregada de alta energia e fóton de baixa energia. Essas interações finalmente resultaram em matéria e radiação em equilíbrio térmico.

Equilíbrio térmico

Em equilíbrio térmico, a radiação obedece ao Planck Distribution of Energy,

$$ B_v (T) = \ frac {2hv ^ 3} {c (e ^ {hv / k_BT} -1)} $$

Durante esse tempo, devido às interações altamente frequentes, o caminho livre médio dos fótons era muito pequeno. O universo era opaco à radiação. O universo inicial era dominado pela radiação. O universo evoluiu de tal forma que a matéria e a radiação atingiram o Equilíbrio Térmico e sua densidade de energia se igualou. Isso pode ser visto no gráfico que mostra a evolução da densidade com o fator de escala. Vamos descobrir o fator de escala (tempo) (a (t)) em que a matéria e a radiação alcançaram o equilíbrio.

$$ \ rho_m \ propto \ frac {1} {a ^ 3}, \: \ rho_r \ propto \ frac {1} {a ^ 4} $$

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = \ frac {\ Omega_ { m, 0}} {\ Omega_ {r, 0}} a (t) $$

Em equilíbrio,

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = 1 $$

$$ \ Rightarrow \ frac {\ Omega_ {m, 0}} {\ Omega_ {r, 0}} a (t) = 1 \: \ Rightarrow a (t) = 2,96 \ vezes 10 ^ {- 4} $$

usando $ \ Omega_ {m, 0} = 0,27 $ e $ \ Omega_ {r, 0} = 8 \ vezes 10 ^ {- 5} $. O deslocamento para o vermelho correspondente a este fator de escala é dado por -

$$ z = 1 / a (t) -1 \ aprox. 3375 $$

A densidade de energia da radiação diminuiu devido à expansão do universo. Assim, o universo começou a esfriar. Conforme a energia dos fótons começou a diminuir, átomos neutros começaram a se formar. Assim, por volta de um desvio para o vermelho de 1300, o hidrogênio neutro começou a se formar. Esta era tinha uma temperatura próxima a 3000K.

A interação entre matéria e radiação tornou-se muito rara e, assim, o universo começou a se tornar transparente à radiação. Este período de tempo é chamado“Surface of last scattering”como o caminho livre médio dos fótons tornou-se muito grande, devido ao qual quase nenhum espalhamento ocorreu após este período. Também é chamado de“Cosmic Photosphere”.

Pontos para lembrar

• O CMB é constituído pelos fótons da época em que a matéria e a radiação estavam em equilíbrio.

• O universo primitivo era muito quente e a energia muito alta para que a matéria permanecesse neutra, então existia como matéria ionizada - plasma.

• Dispersão Compton, Dispersão Thomson, Dispersão Compton Inversa foram os 3 processos de interação matéria-radiação então.

• O universo evoluiu de tal forma que a matéria e a radiação alcançaram o equilíbrio térmico.

Devemos primeiro entender o que caracteriza o decoupling. Sabemos que as energias eram muito mais elevadas a tal ponto que a matéria existia apenas na forma deIonized Particles. Assim, nas épocas de desacoplamento e recombinação, a energia tinha que cair para permitir a ionização do hidrogênio. Um cálculo aproximado pode ser feito para a estimativa da temperatura no momento do desacoplamento.

Isso foi realizado da seguinte forma -

Primeiro, considere apenas a ionização do hidrogênio do estado fundamental.

$$ hv \ approx k_BT $$

$$ \ portanto, T \ approx \ frac {hv} {k_B} $$

Para ionização do hidrogênio do estado fundamental, hν é 13,6 eV e kB é o Boltzmann Constant8,61 × 10 ⁻⁵ eV / K que revela que a temperatura é 1,5 × 105 kelvin.

Isso basicamente nos diz que se a temperatura estiver abaixo de 1,5 × 10 ⁵ K, os átomos neutros podem começar a se formar.

Sabemos que a proporção de fótons para bárions é de cerca de 5 × 10 ¹⁰ . Portanto, mesmo na cauda do gráfico, onde o número de fótons reduz, ainda haverá fótons suficientes para ionizar os átomos de hidrogênio. Além disso, a recombinação de elétron e próton não garante um átomo de hidrogênio no estado fundamental. Estados excitados requerem menos energia para ionização. Portanto, uma análise estatística disciplinada deve ser realizada caso a caso para obter um valor preciso. Os cálculos definem a temperatura para cerca de 3000K.

Para fins de explicação, consideramos o caso da excitação do hidrogênio no primeiro estado excitado. A expressão geral para a razão do número de fótons com energia maior queΔE, Nγ (> ΔE) para o número total de fótons Nγ é dado por -

$$ \ frac {N_ \ gamma (> \ Delta E)} {N_ \ gamma} \ propto e ^ {\ frac {- \ Delta E} {kT}} $$

Para o caso de excitação de hidrogênio para o primeiro estado excitado, ΔEé 10,2 eV. Agora, se considerarmos um número altamente conservador de pelo menos 1 fóton com energia superior a 10,2 para cada bárion (tendo em mente que a razão é 5 × 10 ¹⁰ , obtemos a temperatura da equação 3 como 4800 K (Nγ inserido (> ΔE) = Np).

Esta é a temperatura para criar uma população de átomos de hidrogênio neutros no primeiro estado excitado. A temperatura para ionizar isso é significativamente menor. Assim, obtemos uma estimativa melhor do que 1,5 × 10 ⁵ K que está mais próxima do valor aceito de 3000 K.

Redshift - Relação de temperatura

Para compreender a relação entre o desvio para o vermelho e a temperatura, empregamos os dois métodos a seguir, conforme descrito abaixo.

Método 1

De Wien’s Law, nós sabemos isso

$$ \ lambda_mT = constante $$

Para relacionar isso ao redshift, usamos -

$$ 1 + z = \ frac {\ lambda_0} {\ lambda_e} $$

Como $ λ_oT_o = λ_eT (z) $, obtemos -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Configuração T_o como o valor atual 3K, podemos obter valores de temperatura para um determinado desvio para o vermelho.

Método 2

Em termos de frequência, sabemos -

$$ v_0 = \ frac {v_e} {1 + z} $$

$$ B_vdv = \ frac {2hv ^ 3} {c ^ 2} \ frac {dv} {e ^ {hv / kT} -1} $$

Isso nos fala sobre a energia líquida dos fótons para um intervalo de energia e hνé a energia de um único fóton. Portanto, podemos obter o número de fótons porBνdν/hν.

Se $ n_ {νo} $ é para presente e $ n_ {νe} $ para emitido, obtemos -

$$ \ frac {n_ {v_e}} {n_ {v_0}} = (1 + z) ^ 3 $$

Na simplificação, obtemos,

$$ n_ {v_0} = \ frac {2v_c ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} \ frac {1} {(1 + z) ^ 3} = \ frac {2v_0 ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} $$

Isso nos dá o Wien’s Law novamente e, portanto, pode-se concluir que -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Pontos para lembrar

• O universo inicial era muito quente, ∼ 3000K.
• As medições atuais revelam que a temperatura do universo está perto de 3K.
• Quanto mais recuamos no tempo, a temperatura aumenta proporcionalmente.

Neste capítulo, discutiremos a anisotropia da radiação CMB e do COBE, ou seja, Cosmic Background Explorer.

Anisotropias primárias na CMB

Para entender as observações do espaço e as anisotropias primárias na radiação cósmica de fundo da micro-ondas, tomemos as seguintes equações e entendamos como mostrado abaixo.

Densidade numérica de fótons CMB (n _γ , 0)

$$ n _ {\ gamma, 0} = \ frac {Total \: energia \: densidade} {Característica \: energia \: de \: Fótons} $$

$$ n _ {\ gamma, 0} = \ frac {aT_0 ^ 4} {k_BT_0} $$

Onde $ k_B $ está Boltzmann Constant e $ T_0 $ é o present temperature of the universe.

Usando a temperatura atual $ (T_0) $ como 2,7 K, obtemos a densidade de número de fótons CMB atual como 400 cm ^-3 .

A densidade numérica de fótons estelares cósmicos é muito menor (∼ = 10 ⁻³ cm ⁻³ ) em grandes escalas.

Razão de barião para fóton (η)

Se as contribuições estelares de galáxias, que se misturam com CMB, são insignificantes, a proporção de bárions para prótons é -

$$ \ eta = \ frac {n_ {b, 0}} {n _ {\ gamma, 0}} $$

O valor atual é ∼5 × 10 ⁻¹⁰ . Uma vez que as densidades de número de fótons e bárions são proporcionais aa⁻³, então η não evolui com o tempo.

Densidade de energia

Ao contrário da densidade numérica, a densidade de energia da matéria é mais dominada do que a densidade de energia do fóton atualmente.

A densidade de energia da matéria bariônica = $ \ rho_ {b, 0} c ^ 2 = 0,04 \ rho_cc ^ 2 = 2 × 10 ^ {- 9} ergcm ^ {- 3} $. Enquanto, a densidade de energia da radiação = $ aT_0 ^ 4 = 4 \ vezes 10 ^ {- 13} ergcm {−3} $.

Isotropia da radiação CMB

Penzias e Wilsondescobriram que o CMB é isotrópico dentro dos limites das observações. Os limites são baixa resolução angular e sensibilidade dos instrumentos. Eles fizeram observações da Terra, devido a isso, as observações não podem ser feitas em todo o espectro, pois o vapor de água na atmosfera absorve muitos comprimentos de onda que variam de 1 mm a 1 m. Portanto, o CMB não pode ser afirmado como um espectro.

O CMB é considerado rotacionalmente invariante (isotrópico). Visto que existiu um tempo em que a matéria e a radiação estavam em equilíbrio, a formação de estruturas no universo é inexplicável. Uma vez que a distribuição da matéria não é isotrópica, mas é agrupada como uma teia cósmica com enormes vazios entre eles, acredita-se que a CMB tenha uma origem extragalática.

Mas, a partir do início das observações do espaço, foram encontradas anisotropias na CMB, o que levou ao raciocínio de que essas anisotropias na matéria levam à formação de estruturas.

Observação da radiação CMB do espaço

Os principais satélites lançados para observar o CMB foram -

• Cosmic Microwave Background Explorer (COBE, 1989)

• Wilkinson Microwave Anisotropy Probe (WMAP, 2001) e

• Planck (2009).

COBE (Explorador do Fundo Cósmico)

O COBE tinha principalmente dois instrumentos. Eles eramFar InfraRed Absolute Spectrometer (FIRAS) e Differential Microwave Radiometers(Antenas DMR). O FIRAS mede a intensidade do CMB como uma função do comprimento de onda ao longo de qualquer direção específica. Considerando que, DMR tem 3 antenas para medir a diferença de intensidade de CMB de três direções diferentes. As dicas a seguir nos fornecem mais informações sobre FIRAS e DMR.

• As observações CMB do FIRAS mostram que a radiação CMB corresponde ao espectro do corpo negro em T = 2,72528 ± 0,00065 K.

• O DMR mede três frequências (31,5 GHz, 53 GHz, 90 GHz) em todas as direções no céu.

• O “símbolo do batman vermelho” nas observações do DMR é o ruído da emissão do primeiro plano (emissão síncrotron difusa galáctica).

• As variações de intensidade nas observações correspondem às variações de temperatura. A presença de pontos quentes e frios prova que a radiação CMB é anisotrópica.

• Esta anisotropia deve estar presente no momento do desacoplamento, pois não há distorções na CMB. Portanto, a matéria deveria ter alguns bolsões com densidade maior do que os outros.

Resultados COBE

O espectro CMB (intensidade em função da energia) é quase um corpo negro perfeito correspondendo a T = 2,7 K. A intensidade específica da radiação CMB é quase a mesma para todas as direções. A confirmação de que o universo é isotrópico em grandes escalas (valida nossa suposição do princípio cosmológico).

A análise dos dados mostrou que existem anisotropias de temperatura (“flutuações”) no espectro CMB na resolução do COBE (DMR).

Resolution of COBE, WMAP, Planck

• O instrumento DMR on-board COBE tinha uma resolução espacial limite (máxima) de ± 7 graus.

• A Sonda de Anisotropia de Microondas Wilkinson (WMAP) teve uma resolução média de ± 0,7 graus.

• O satélite Planck tem uma resolução angular de ± 10 arc-minuto.

Pontos para lembrar

• A densidade numérica de fótons estelares cósmicos é muito menor do que a densidade numérica de fótons CMB.

• Vivemos em um universo dominado pela matéria, uma vez que a densidade de energia da matéria é maior do que a densidade de energia do fóton.

• COBE, WMAP, Planck são esforços para medir e quantificar anisotropias na CMB.

• A formação da estrutura do universo é resultado das anisotropias CMB.

Quando olhamos para o mapa CMB refinado e corrigido em todo o céu, há muita contaminação de primeiro plano, que é uma espécie de anisotropynesses mapas. Podemos ver que essas emissões em primeiro plano são da galáxia da Via Láctea. A intensidade do CMB é alta ao longo do plano do plano galáctico e diminui à medida que nos afastamos. Nestes, podemos observar anisotropias secundárias, que são emissões síncrotron da galáxia. Essas emissões constituem a contaminação do primeiro plano. Para observar a emissão CMB do céu, precisamos subtrair essas emissões do primeiro plano.

A imagem a seguir mostra o CMB com emissões de primeiro plano.

Anisotropia dipolar

Existe um outro tipo de anisotropia, que foi encontrado no mapa do céu CMB, é chamado de anisotropia dipolo. Não está associado ao universo primitivo. Isso pode ser representado usando funções harmônicas esféricas. Se houver um padrão na superfície esférica e quisermos mapeá-lo usando funções matemáticas, podemos fazer isso usando funções trigonométricas. Assim, quando mapeamos, pode ser um monopolo - o mesmo em todas as direções, ou um dipolo - inverte as propriedades quando girado em 180 graus. Da mesma forma, temos quadrupolo e assim por diante. Para um padrão complexo, pode ser expresso como a soma destes monopolo, dipolo, quadrupolo, etc.

O CMB é modelado de tal maneira que uma das principais fontes de anisotropia no mapa do céu é esta anisotropia dipolo, mas não é a modelagem primordial do CMB. Isso pode ser visto na imagem abaixo.

A direção do dipolo que vemos não é uma direção aleatória. A anisotropia dipolar tem uma direção. Vemos a intensidade CMB ao longo de uma direção específica. Essa direção se deve ao vetor velocidade do sistema solar. A velocidade da terra pode ser representada em relação ao sol ou ao centro da galáxia. Na direção em que a terra está se movendo, observamos um Blueshift e um Redshift e o dipolo está ao longo desta direção.

A imagem acima tem uma aparência típica de dipolo porque nossa Galáxia está se movendo em uma direção específica. O resultado é - um lado do céu aparecerá desviado para vermelho e o outro lado do céu aparecerá desviado para azul. Nesse caso, o deslocamento para o vermelho significa que os fótons são mais longos em comprimento de onda = mais frio (portanto, ao contrário de seus nomes, eles parecem azuis no diagrama acima).

Podemos dizer que a Terra está se movendo em alguma direção específica em relação ao sol / centro galáctico / CMB no céu em um determinado instante. Então, se olharmos para qualquer ângulo e medirmos a temperatura do CMB, seria diferente. Isso ocorre porque estamos medindo fótons que são desviados para o azul ou para o vermelho e dependem da linha de visão dos fótons no céu.

Pontos para lembrar

• A contaminação do primeiro plano no mapa do céu de CMB é chamada de anisotropia de CMB.

• Essas emissões são provenientes de nossa própria galáxia, a Via Láctea.

• Os 2 tipos de anisotropias são: anisotropia de dipolo e anisotropia de espectro de potência angular.

• A anisotropia dipolar está em uma direção específica, enquanto a anisotropia do espectro de potência angular está espalhada por toda parte.

O comprimento do horizonte é a distância percorrida pelos fótons de luz de 'The Big Bang' a 'The Recombination Era'. O 1 ^r pico do espectro angular está em θ = 1◦ (L = 180), que é uma escala de comprimento muito especial.

A distância adequada entre dois pontos é dada por -

$$ r_p = \ int_ {0} ^ {t} cdt $$

Quando tomamos o período de tempo de t = 0 para t = t _rec , então

$$ r_H = \ int_ {0} ^ {t_ {rec}} cdt $$

Onde $ r_H $ é a distância adequada do horizonte.

Agora, sabemos que -

$$ \ dot {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ dt = \ frac {da} {\ ponto {a}} $$

Quando t = 0, a = 0.

Então $ t = t_ {rec}, a = a_0 / (1 + z_ {rec}) $.

Portanto, podemos escrever,

$$ r_H (z_ {rec}) = \ int_ {0} ^ {a_ {rec}} c \ frac {da} {aH} $$

$$ H (a_ {rec}) = H (z_ {rec}) = H_0 \ sqrt {\ Omega_ {m, 0}} a ^ {- 3/2} $$

Durante o Recombination period universefoi dominado pela matéria. ie,Ωrad << Ωmatter. Portanto, o termo radiação é abandonado.

$$ r_H (z_ {rec}) = \ frac {c} {H_0 \ sqrt {\ Omega_ {m, 0}}} \ int_ {0} ^ {a_ {rec}} \ frac {da} {a ^ { -1/2}} $$

$$ r_H (z_ {rec}) = \ frac {2c} {3H_0 \ sqrt {\ Omega_ {m, 0}}} \ frac {1} {(1 + z_ {rec}) ^ {3/2}} $$

$$ \ theta_H (rec) = \ frac {r_H (z_ {rec})} {d_A (z_ {rec})} $$

O que é igual a 0,5 grau, se colocarmos todos os valores conhecidos na equação.

o Electromagnetic radiationé opaco da superfície da última dispersão. Quaisquer dois pontos "não" situados no horizonte um do outro não precisam ter as mesmas propriedades. Portanto, ele fornecerá diferentes valores de temperatura.

Podemos obter dois pontos nesta superfície que não se cruzaram, o que significa que em um ponto o universo se expandiu mais rápido do que a velocidade da luz, que é o modelo inflacionário de expansão.

Pontos para lembrar

• O comprimento do horizonte é a distância percorrida pelos fótons de luz de 'The Big Bang' a 'The Recombination Era'.

• Durante o período de Recombinação, o universo foi dominado pela matéria.

• A radiação eletromagnética é opaca da superfície do último espalhamento.

Astrobiologyé o estudo da origem, evolução, distribuição e futuro da vida no universo. Está preocupado em descobrir e detectarExtrasolar Planets.

Astrobiology aborda os seguintes pontos -

• Como a vida começa e evolui? (biologia + geologia + química + ciências atmosféricas)

• Existem mundos além da terra que são favoráveis ​​para a vida? (astronomia)

• Qual seria o futuro da vida na terra?

Astronomy aborda os seguintes pontos -

• Como detectar o sistema planetário em torno de outras estrelas?

• Um dos métodos é a imagem direta, mas é uma tarefa muito difícil porque os planetas são fontes de luz extremamente tênues em comparação com as estrelas, e a pouca luz que vem deles tende a se perder no brilho de sua estrela-mãe.

• O contraste é melhor quando o planeta está mais próximo de sua estrela-mãe e quente, de modo que emite radiação infravermelha intensa. Podemos fazer imagens na região do infravermelho.

Técnicas para detecção de planeta extra-solar

As técnicas mais eficientes para detecção de planetas extra-solares são as seguintes. Cada um deles também é explicado em detalhes nos capítulos subsequentes.

Método de Velocidade Radial

É também chamado de método Doppler. Neste -

• O sistema de planetas estelares gira em torno de seu baricentro, as estrelas oscilam.

• Wobbling pode ser detectado por

  • Mudanças periódicas de vermelho / azul. Astrometria - mede os objetos no céu com muita precisão.

Método de Trânsito

Método de trânsito (telescópio espacial Kepler) é usado para descobrir o tamanho. A queda no brilho de estrela por planeta é geralmente muito menor, ao contrário de um sistema binário.

Imagem Direta

Imaginando o planeta usando um telescópio.

Vejamos um estudo de caso feito sobre o Método da Velocidade Radial.

Estudo de caso

Este estudo de caso é sobre a órbita circular e o plano da órbita perpendicular ao plano do céu. O tempo gasto por ambos ao redor do baricentro será o mesmo. Será igual à diferença de tempo entre dois Redshift ou Blueshift.

Considere a seguinte imagem.

Em A e C - a velocidade total é medida. Em C, a velocidade é zero.

• Vrmax = V _* é a velocidade verdadeira da estrela.

• P é o período de tempo da estrela e também do planeta.

• θ é a fase da órbita.

• Massa estelar - M _* , raio da órbita a _* , massa do planetam_p.

Da equação do centro de massa,

$$ m_p a_p = M_ \ ast a_ \ ast $$

Da equação de velocidade,

$$ V_ \ ast = \ frac {2 \ pi a_ \ ast} {P} $$

$$ \ Rightarrow a_ \ ast = \ frac {PV_ \ ast} {2 \ pi} $$

De Kepler’s Law,

$$ P ^ 2 = \ frac {4 \ pi ^ 2a_p ^ 3} {GM_ \ ast} $$

$$ \ Rightarrow a_p = \ left (\ frac {P ^ 2GM_ \ ast} {4 \ pi ^ 2} \ right) ^ {1/3} $$

A partir das equações acima, obtemos -

$$ \ Rightarrow m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {1/3} M_ \ ast ^ {2/3} V_ \ ast $$

Obtemos: $ m_p, a_p $ e $ a_ \ ast $.

A equação acima é tendenciosa para a maioria dos planetas massivos próximos à estrela.

Pontos para lembrar

• Astrobiologia é o estudo da origem, evolução, distribuição e futuro da vida no universo.

• As técnicas para detectar os planetas extrasolares são: Método de Velocidade Radial, Método de Trânsito, Imagem Direta, etc.

• Wobbling pode ser detectado por mudanças periódicas de vermelho / azul e astrometria.

• O Radial Velocity Method tende a detectar planetas massivos próximos à estrela.

No capítulo anterior, o Método da Velocidade Radial para o caso em que o plano orbital e o plano do céu são perpendiculares foi discutido para órbitas circulares. Aqui, lidamos com mais um caso, em que o plano orbital e o plano do céu não são perpendiculares para órbitas circulares.

Quando o plano orbital está em um ângulo em relação ao plano do céu (não perpendicular), temos a seguinte situação -

Nesse caso, quando eles eram perpendiculares, tínhamos dois pontos nos quais podíamos medir a velocidade real. Mas aqui, isso não é possível. Em todos os pontos, podemos medir apenas um componente da velocidade verdadeira,v.

$$ v_r = v \: sin (i) cos (\ theta) $$

Onde θé a fase da órbita, que é uma quantidade dependente do tempo. O ângulo de inclinaçãoipor outro lado, é independente do tempo. Conseqüentemente,

$$ (v_r) _ {max} = v \: sin (i) $$

A curva de velocidade radial observada será da seguinte forma -

Quando o plano orbital é perpendicular ao céu -

$$ m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3}} v $ $

Onde m_p, P, G, M∗são massa do planeta, período orbital, constante gravitacional universal e massa da estrela, respectivamente. Mas, neste caso, devemos modificá-lo da seguinte forma -

$$ m_psin (i) = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3} } (v_r) _ {max} $$

Porém, encontrar o valor de i é uma tarefa difícil. Podemos impor certas restrições ao valor deiusando o método de trânsito. A passagem do planeta entre a estrela e a Terra é chamada de trânsito. Podemos obter a curva de luz observando um trânsito e uma queda significativa no fluxo observado de uma curva de luz implica que i está perto de 90 graus. Se tais condições não forem satisfeitas, não podemos ter nenhuma ideia sobre o valor dei. Então o valor dem_p que encontramos pode servir como um limite inferior para a massa do planeta, uma vez que é realmente m_p sin(i) e sin(i) ≤ 1.

Para concluir, o método da velocidade radial é mais conveniente do que o método de trânsito porque a velocidade radial pode ser medida a qualquer momento, mas as medições de trânsito podem ser feitas apenas durante o trânsito, que pode não durar muito.

Pontos para lembrar

• Encontrar a inclinação da órbita do planeta não é alcançado pelo método da Velocidade Radial.

• O método de velocidade radial é melhor do que o método de trânsito porque a velocidade radial pode ser medida sempre ao contrário dos trânsitos.

• Os trânsitos têm curta duração e são muito fáceis de perder.

O Método de Trânsito (Kepler Space Telescope)é usado para descobrir o tamanho. A queda no brilho de uma estrela por um planeta é geralmente muito menos diferente de um sistema binário.

• F₀ é o fluxo da estrela antes que o planeta o oculte.

• F₁ é o fluxo depois que o planeta inteiro está na frente da estrela.

A imagem a seguir será usada para todos os cálculos.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$

$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ cong 0,001 \% $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {júpiter} \ cong 1 \% $$

Isso não é fácil de conseguir com um telescópio terrestre. Isso é alcançado pelo telescópio Hubble.

Aqui, $ t_T $ é o tempo entre as posições A e D e $ t_F $ é o tempo entre as posições B e C.

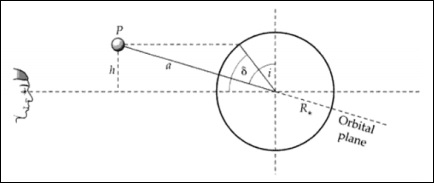
A geometria de um trânsito em relação à inclinação ido sistema. A latitude e a inclinação do trânsito são intercambiáveis.

A partir das imagens acima, podemos escrever -

$$ \ frac {h} {a} = cos (i) $$

$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$

$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$

$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$

$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$

$$ sin (\ theta) = \ frac {y} {a} $$

$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$

$$ t_T = \ frac {P} {2 \ pi} \ vezes 2 \ theta $$

Aqui, $ t_T $ é a fração de um período de tempo para o qual o trânsito acontece e (2θ / 2π) é a fração do ângulo para o qual o trânsito acontece.

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Normalmente, um >> R ∗ >> Rp. Então, podemos escrever -

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Aqui, Pé a duração entre dois trânsitos sucessivos. O tempo de trânsito é muito menor em comparação com o período de tempo orbital. Conseqüentemente,

$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$

Aqui, t_T, P, R∗ são os observáveis, a e i deve ser descoberto.

Agora,

$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

onde, $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.

Deixei,

$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$

Agora, podemos expressar,

$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$

Para as estrelas da sequência principal,

$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$

$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$

Isto dá R∗.

Portanto, obtemos o valor de 'a' também.

Então, temos 'R _p ', 'ap' e até mesmo 'i'.

Por tudo isso,

$$ h \ leq R_ \ ast + R_p $$

$$ a \: cos \: i \ leq R_ \ ast + R_p $$

Mesmo para ~ 89 graus, a duração do trânsito é muito pequena. O planeta deve estar muito próximo para ter um tempo de trânsito suficiente. Isso fornece uma restrição rígida em 'i'. Assim que obtivermos 'i', podemos derivar 'm _p ′ da medição da velocidade radial.

Essa detecção pelo método de trânsito é chamada de detecção de chance, ou seja, probabilidade de observar um trânsito. Os cálculos da probabilidade de trânsito (probabilidade de observação) são mostrados abaixo.

A probabilidade de trânsito está relacionada ao ângulo sólido traçado pelas duas configurações de trânsito extremas, que é -

$$ Sólido \: ângulo \: de \: planeta \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$

Bem como o ângulo sólido total em um semi-eixo maior a, ou -

$$ Sólido \: ângulo \: de \: esfera \: = \: 4 \ pi $$

A probabilidade é a proporção dessas duas áreas -

$$ = \: \ frac {área \: de \: céu \: coberto \: por \: favorável \: orientação} {área \: de \: céu \: coberto \: por \: todos \: possível \: orientação \: de \: órbita} $$

$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: of \: hollow \: cyclinder} {area \ : de \: esfera} $

Essa probabilidade é independente do observador.

Pontos para lembrar

• O Método de Trânsito (Telescópio Espacial Kepler) é usado para descobrir o tamanho.
• A detecção pelo método de trânsito é uma detecção casual.
• O planeta deve estar muito próximo para obter tempo de trânsito suficiente.
• A probabilidade de trânsito está relacionada ao ângulo sólido do planeta.
• Esta probabilidade é independente do quadro de referência do observador.

A primeira imagem direta de um planeta extrassolar, em 2004, era de um planeta de massa 3-10 M_jupiter orbitando em torno de uma anã marrom (2M1207) com uma massa de 25 M_jupiter. Técnicas como velocidade radial, trânsito, microlente gravitacional, imagem, astrometria, etc., têm sido usadas para a detecção de exoplanetas. O número de detecções vem aumentando a cada ano.

Até por volta de 2010, o método da velocidade radial era amplamente usado, mas agora a maioria das detecções são feitas pelo método de trânsito. Houve um aumento no número de detecções em 2014, que foi quandoKepler Space Telescope (KST) começou a dar os resultados.

Uma distribuição de período de massa mostra que o método de velocidade radial é mais inclinado para a detecção de planetas massivos com um período maior, enquanto usando o método de trânsito, planetas com período inferior são detectados apenas como mostrado na imagem a seguir (Cortesia: NASA Exoplanet Archive) .

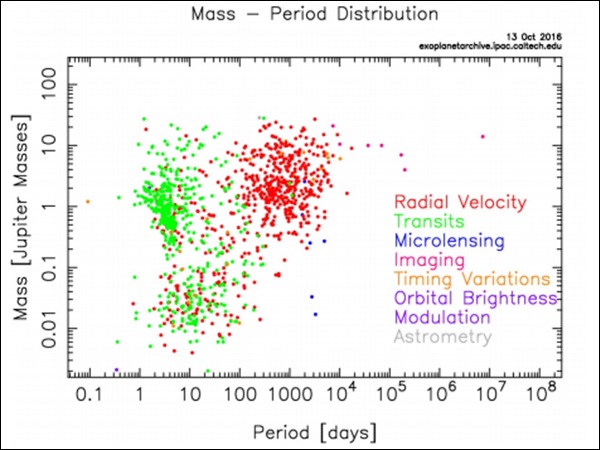
Há um aumento colossal no número de detecção de planetas de massa menor desde o advento do KST. Isso é evidente na figura abaixo. Os planetas detectados pelo KST são divididos em dois grupos: planetas massivos quentes chamados “Júpiteres Quentes” e planetas de massa mais baixa chamados “Super Terras Quentes” (pois são mais massivos que a Terra).

Quando plotamos o número de planetas extra-solares detectados versus a distância a eles, descobrimos que a maioria desses planetas está dentro de 2kpc, o que está bem dentro de nossa galáxia. Talvez os planetas não sejam tão incomuns no universo, uma vez que nossa detecção é limitada a apenas certos tipos de planetas em uma parte muito pequena do universo.

Os planetas são formados a partir de circumstellar disc ou proto planetary disc. Se os planetas são formados como um subproduto durante a formação das estrelas, talvez o número de planetas no universo exceda o número de estrelas no universo !!

Zonas habitáveis

Uma Zona Habitável pode ser definida como a zona ao redor da estrela onde a água pode existir em sua forma líquida. Considere um planeta à distância $ a_p $ da estrela, conforme mostrado na figura a seguir. Um método simples para calcular a temperatura do planeta é descrito a seguir.

$$ \ left (\ frac {L_ \ ast} {4 \ pi a ^ 2_p} \ right) \ pi R ^ 2_p (1 - A) = 4 \ pi R ^ 2_p \ sigma T ^ 4_p $$

e

$$ \ frac {L_ \ ast} {4 \ pi R ^ 2_ \ ast} = \ sigma T ^ 4_ \ ast $$

$$ \ portanto T_p = (1 - A) T_ \ ast \ sqrt {\ frac {R_ \ ast} {2a_p}} $$

No nosso caso, substituir

• L_sun = 3.83 x 10²⁶

• a_p = 1.5 ∗ 10¹¹ and

• A = 0.3

Irá dar $ T_ {Earth} = 255K $. O cálculo real é muito complexo, o que inclui a física da nuvem. A zona habitável em nosso sistema solar está entre 0,9 UA e 1,7 UA.

Descobriu-se que a luminosidade do Sol estava aumentando com o tempo devido à diminuição da pressão do gás. Era 30% menos brilhante quando começou a queimar hidrogênio. Isso resultaria na mudança da zona habitável para longe do sol. Como a Terra está perto da borda interna da zona habitável, talvez um dia ela se mova para fora da zona!

Zona continuamente habitável

Em suma, é denominado como CHZpode ser definida como a região na qual a água líquida pode existir durante toda a vida útil da Sequência Principal de uma estrela. O KST detectou muitos planetas extrasolares que se encontram na zona habitável.

Uma bioassinatura é qualquer substância - como um elemento, isótopo, molécula ou fenômeno que fornece evidência científica de vida passada ou presente. Um exemplo é a detecção de O ₂ e CO ₂ em um planeta, o que geralmente não é possível apenas por meio de processos geológicos. Esta detecção é feita analisando os espectros de absorção.

Pontos para lembrar

• Técnicas como velocidade radial, trânsito, microlente gravitacional, imagem, astrometria, etc., têm sido usadas para a detecção de exoplanetas.

• O método da velocidade radial é mais inclinado para a detecção de planetas massivos com período maior.

• Os planetas massivos quentes são chamados de “Júpiter Quente” e os planetas de massa inferior são chamados de “Super Terras Quentes”.

• O número de planetas no universo excede o número de estrelas no universo.

• Uma zona habitável pode ser definida como a zona ao redor da estrela onde a água pode existir em sua forma líquida.