Системы управления - Алгебра блок-схем
Алгебра блок-схемы - это не что иное, как алгебра, связанная с основными элементами блок-схемы. Эта алгебра имеет дело с графическим представлением алгебраических уравнений.
Основные соединения для блоков
Между двумя блоками существует три основных типа связи.
Последовательное соединение
Последовательное соединение также называется cascade connection. На следующем рисунке два блока с передаточными функциями $ G_1 (s) $ и $ G_2 (s) $ соединены последовательно.

Для этой комбинации мы получим результат $ Y (s) $ как
$$ Y (s) = G_2 (s) Z (s) $$
Где $ Z (s) = G_1 (s) X (s) $
$$ \ Rightarrow Y (s) = G_2 (s) [G_1 (s) X (s)] = G_1 (s) G_2 (s) X (s) $$
$$ \ Rightarrow Y (s) = \ lbrace G_1 (s) G_2 (s) \ rbrace X (s) $$
Сравните это уравнение со стандартной формой выходного уравнения, $ Y (s) = G (s) X (s) $. Где $ G (s) = G_1 (s) G_2 (s) $.
Это означает, что мы можем представить series connectionиз двух блоков с одним блоком. Передаточная функция этого единственного блока - этоproduct of the transfer functionsэтих двух блоков. Эквивалентная блок-схема показана ниже.
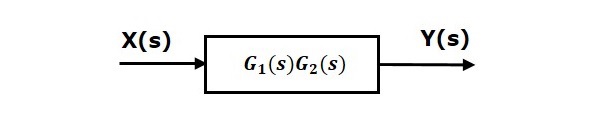
Точно так же вы можете представить последовательное соединение n блоков с одним блоком. Передаточная функция этого единственного блока является продуктом передаточных функций всех этих «n» блоков.
Параллельное соединение
Блоки, соединенные в parallel будет иметь same input. На следующем рисунке два блока с передаточными функциями $ G_1 (s) $ и $ G_2 (s) $ соединены параллельно. Выходы этих двух блоков подключены к точке суммирования.

Для этой комбинации мы получим результат $ Y (s) $ как
$$ Y (s) = Y_1 (s) + Y_2 (s) $$
Где $ Y_1 (s) = G_1 (s) X (s) $ и $ Y_2 (s) = G_2 (s) X (s) $
$$ \ Rightarrow Y (s) = G_1 (s) X (s) + G_2 (s) X (s) = \ lbrace G_1 (s) + G_2 (s) \ rbrace X (s) $$
Сравните это уравнение со стандартной формой выходного уравнения, $ Y (s) = G (s) X (s) $.
Где $ G (s) = G_1 (s) + G_2 (s) $.
Это означает, что мы можем представить parallel connectionиз двух блоков с одним блоком. Передаточная функция этого единственного блока - этоsum of the transfer functionsэтих двух блоков. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить параллельное соединение n блоков с одним блоком. Передаточная функция этого единственного блока представляет собой алгебраическую сумму передаточных функций всех этих "n" блоков.
Обратная связь
Как мы обсуждали в предыдущих главах, существует два типа feedback- положительные отзывы и отрицательные отзывы. На следующем рисунке показана система управления с отрицательной обратной связью. Здесь два блока с передаточными функциями $ G (s) $ и $ H (s) $ образуют замкнутый цикл.

Выход точки суммирования -
$$ E (s) = X (s) -H (s) Y (s) $$
Выход $ Y (s) $ -
$$ Y (s) = E (s) G (s) $$
Подставьте значение $ E (s) $ в приведенное выше уравнение.
$$ Y (s) = \ left \ {X (s) -H (s) Y (s) \ rbrace G (s) \ right \} $$
$$ Y (s) \ left \ {1 + G (s) H (s) \ rbrace = X (s) G (s) \ right \} $$
$$ \ Rightarrow \ frac {Y (s)} {X (s)} = \ frac {G (s)} {1 + G (s) H (s)} $$
Следовательно, передаточная функция замкнутого контура отрицательной обратной связи равна $ \ frac {G (s)} {1 + G (s) H (s)} $
Это означает, что мы можем представить отрицательную обратную связь двух блоков с одним блоком. Передаточная функция этого единственного блока является передаточной функцией замкнутого контура отрицательной обратной связи. Эквивалентная блок-схема показана ниже.

Точно так же вы можете представить соединение двух блоков с положительной обратной связью с одним блоком. Передаточная функция этого отдельного блока является передаточной функцией замкнутого контура положительной обратной связи, то есть $ \ frac {G (s)} {1-G (s) H (s)} $
Алгебра блок-схем для суммирования точек
Есть две возможности сдвига точек суммирования по отношению к блокам:
- Смещение точки суммирования после блока
- Смещение точки суммирования перед блоком
Давайте теперь посмотрим, какие меры необходимо сделать в двух вышеупомянутых случаях один за другим.
Смещение точки суммирования после блока
Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка суммирования находится перед блоком.

Точка суммирования имеет два входа $ R (s) $ и $ X (s) $. Результатом этого будет $ \ left \ {R (s) + X (s) \ right \} $.
Итак, входом в блок $ G (s) $ является $ \ left \ {R (s) + X (s) \ right \} $, а на выходе -
$$ Y (s) = G (s) \ left \ {R (s) + X (s) \ right \} $$
$ \ Rightarrow Y (s) = G (s) R (s) + G (s) X (s) $ (Equation 1)
Теперь переместите точку суммирования после блока. Эта блок-схема показана на следующем рисунке.

Выход блока $ G (s) $ равен $ G (s) R (s) $.
Выход точки суммирования:
$ Y (s) = G (s) R (s) + X (s) $ (Equation 2)
Сравните уравнение 1 и уравнение 2.
Первый член $ 'G (s) R (s)' $ одинаков в обоих уравнениях. Но есть разница во втором члене. Чтобы второй член тоже был таким же, нам потребуется еще один блок $ G (s) $. Он имеет вход $ X (s) $, а выход этого блока задается как вход для точки суммирования вместо $ X (s) $. Эта блок-схема показана на следующем рисунке.
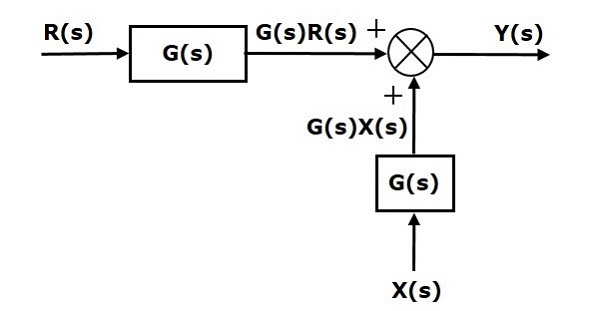
Смещение точки суммирования перед блоком
Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка суммирования стоит после блока.

Выход этой блок-схемы -
$ Y (s) = G (s) R (s) + X (s) $ (Equation 3)
Теперь переместите точку суммирования перед блоком. Эта блок-схема показана на следующем рисунке.

Выход этой блок-схемы -
$ Y (S) = G (s) R (s) + G (s) X (s) $ (Equation 4)
Сравните уравнение 3 и уравнение 4,
Первый член $ 'G (s) R (s)' $ одинаков в обоих уравнениях. Но есть разница во втором члене. Чтобы второе слагаемое было таким же, нам потребуется еще один блок $ \ frac {1} {G (s)} $. Он имеет вход $ X (s) $, а выход этого блока задается как вход для точки суммирования вместо $ X (s) $. Эта блок-схема показана на следующем рисунке.

Алгебра блок-схем для точек взлета
Есть две возможности смещения точек взлета относительно блоков:
- Смещение точки взлета после блока
- Смещение точки взлета перед блоком
Давайте теперь посмотрим, какие меры следует предпринять в двух вышеупомянутых случаях, один за другим.
Смещение точки взлета после блока
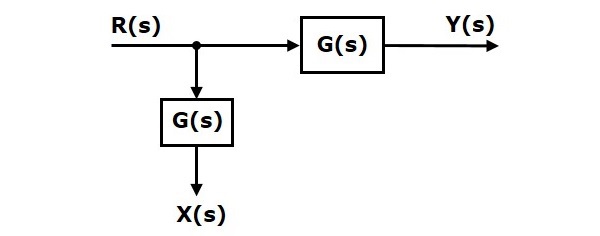
Рассмотрим блок-схему, показанную на следующем рисунке. В этом случае точка взлета находится перед блоком.

Здесь $ X (s) = R (s) $ и $ Y (s) = G (s) R (s) $
Когда вы перемещаете точку взлета после блока, результат $ Y (s) $ будет таким же. Но есть разница в стоимости $ X (s) $. Итак, чтобы получить то же значение $ X (s) $, нам потребуется еще один блок $ \ frac {1} {G (s)} $. Он имеет вход $ Y (s) $, а выход - $ X (s) $. Эта блок-схема показана на следующем рисунке.

Смещение точки взлета перед блоком
Рассмотрим блок-схему, показанную на следующем рисунке. Здесь точка взлета присутствует после блока.

Здесь $ X (s) = Y (s) = G (s) R (s) $
Когда вы перемещаете точку взлета перед блоком, результат $ Y (s) $ будет таким же. Но есть разница в стоимости $ X (s) $. Итак, чтобы получить такое же значение $ X (s) $, нам потребуется еще один блок $ G (s) $. Он имеет вход $ R (s) $, а выход $ X (s) $. Эта блок-схема показана на следующем рисунке.