Системы управления - блок-схемы
Блок-схемы состоят из одного блока или комбинации блоков. Они используются для представления систем управления в наглядной форме.
Основные элементы блок-схемы
Основные элементы блок-схемы - это блок, точка суммирования и точка взлета. Давайте рассмотрим блок-схему замкнутой системы управления, как показано на следующем рисунке, чтобы идентифицировать эти элементы.

Приведенная выше блок-схема состоит из двух блоков, имеющих передаточные функции G (s) и H (s). У него также есть одна точка суммирования и одна точка взлета. Стрелки указывают направление потока сигналов. Давайте теперь обсудим эти элементы один за другим.
Блокировать
Передаточная функция компонента представлена блоком. Блок имеет один вход и один выход.
На следующем рисунке показан блок, имеющий вход X (s), выход Y (s) и передаточную функцию G (s).

Передаточная функция, $ G (s) = \ frac {Y (s)} {X (s)} $
$$ \ Rightarrow Y (s) = G (s) X (s) $$
Выход блока получается умножением передаточной функции блока на вход.
Суммирующая точка
Точка суммирования представлена кружком с крестом (X) внутри. Он имеет два или более входа и один выход. Он производит алгебраическую сумму входных данных. Он также выполняет суммирование или вычитание или комбинацию суммирования и вычитания входных данных на основе полярности входов. Давайте посмотрим на эти три операции одну за другой.
На следующем рисунке показана точка суммирования с двумя входами (A, B) и одним выходом (Y). Здесь входы A и B имеют положительный знак. Таким образом, точка суммирования дает результат Y какsum of A and B.
т.е. Y = A + B.

На следующем рисунке показана точка суммирования с двумя входами (A, B) и одним выходом (Y). Здесь входы A и B имеют противоположные знаки, т. Е. A имеет положительный знак, а B имеет отрицательный знак. Итак, точка суммирования дает результатY как difference of A and B.
Y = A + (-B) = A - B.

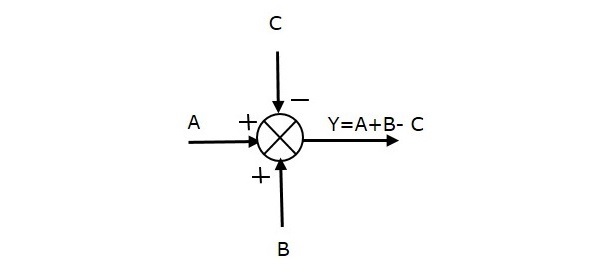
На следующем рисунке показана точка суммирования с тремя входами (A, B, C) и одним выходом (Y). Здесь входы A и B имеют положительный знак, а C - отрицательный. Итак, точка суммирования дает результатY в качестве
Y = A + B + (−C) = A + B - C.
Точка взлета
Точка взлета - это точка, из которой один и тот же входной сигнал может проходить более чем через одну ветвь. Это означает, что с помощью точки взлета мы можем применить один и тот же ввод к одному или нескольким блокам, суммируя точки.
На следующем рисунке точка взлета используется для подключения того же входа R (s) к еще двум блокам.

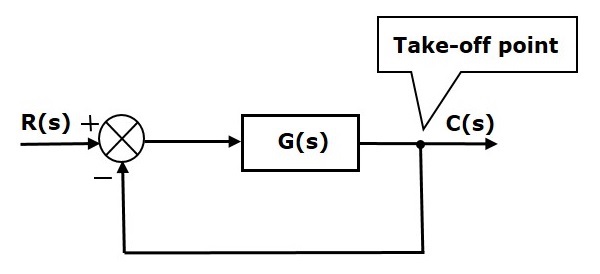
На следующем рисунке точка взлета используется для подключения выхода C (s) в качестве одного из входов к точке суммирования.
Блок-схема представления электрических систем
В этом разделе давайте представим электрическую систему с блок-схемой. Электрические системы содержат в основном три основных элемента -resistor, inductor and capacitor.
Рассмотрим последовательность цепей RLC, как показано на следующем рисунке. Где V i (t) и V o (t) - входные и выходные напряжения. Пусть i (t) - ток, протекающий по цепи. Эта схема находится во временной области.

Применяя преобразование Лапласа к этой схеме, мы получим схему в s-области. Схема показана на следующем рисунке.
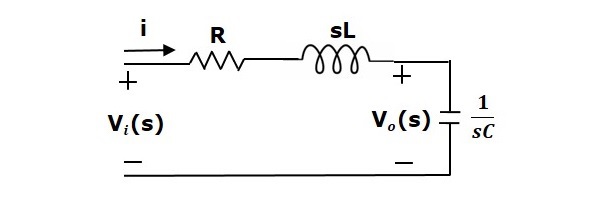
Из приведенной выше схемы мы можем написать
$$ I (s) = \ frac {V_i (s) -V_o (s)} {R + sL} $$
$ \ Rightarrow I (s) = \ left \ {\ frac {1} {R + sL} \ right \} \ left \ {V_i (s) -V_o (s) \ right \} $ (Equation 1)
$ V_o (s) = \ left (\ frac {1} {sC} \ right) I (s) $ (Equation 2)
Давайте теперь нарисуем блок-схемы для этих двух уравнений по отдельности. А затем объедините эти блок-схемы должным образом, чтобы получить общую блок-схему серии RLC Circuit (s-домен).
Уравнение 1 может быть реализовано с помощью блока, имеющего передаточную функцию, $ \ frac {1} {R + sL} $. Вход и выход этого блока - $ \ left \ {V_i (s) -V_o (s) \ right \} $ и $ I (s) $. Нам нужна точка суммирования, чтобы получить $ \ left \ {V_i (s) -V_o (s) \ right \} $. Блок-схема уравнения 1 показана на следующем рисунке.

Уравнение 2 может быть реализовано с помощью блока, имеющего передаточную функцию, $ \ frac {1} {sC} $. Входом и выходом этого блока являются $ I (s) $ и $ V_o (s) $. Блок-схема уравнения 2 показана на следующем рисунке.

Общая блок-схема серии цепей RLC (s-домен) показана на следующем рисунке.

Точно так же вы можете нарисовать block diagram любой электрической цепи или системы, просто следуя этой простой процедуре.
Преобразуйте электрическую схему временной области в электрическую схему s-области, применив преобразование Лапласа.
Запишите уравнения для тока, проходящего через все элементы последовательной ветви, и напряжения на всех шунтирующих ответвлениях.
Нарисуйте блок-схемы для всех вышеперечисленных уравнений по отдельности.
Правильно объедините все эти блок-схемы, чтобы получить общую блок-схему электрической схемы (s-домен).