การวิเคราะห์ข้อมูลทางการเงินของ Excel

คุณสามารถทำการวิเคราะห์ทางการเงินด้วย Excel ได้อย่างง่ายดาย Excel มีฟังก์ชันทางการเงินมากมายให้คุณเช่น PMT, PV, NPV, XNPV, IRR, MIRR, XIRR และอื่น ๆ ที่ช่วยให้คุณได้รับผลการวิเคราะห์ทางการเงินอย่างรวดเร็ว

ในบทนี้คุณจะได้เรียนรู้ว่าคุณสามารถใช้ฟังก์ชันเหล่านี้สำหรับการวิเคราะห์ของคุณได้ที่ไหนและอย่างไร

เงินรายปีคืออะไร?

เงินรายปีคือชุดของการจ่ายเงินสดคงที่ในช่วงเวลาต่อเนื่อง ตัวอย่างเช่นการออมเพื่อการเกษียณเงินประกันเงินกู้บ้านการจำนอง ฯลฯ ในฟังก์ชันเงินงวด -

• จำนวนบวกแสดงถึงเงินสดที่ได้รับ
• จำนวนลบหมายถึงเงินสดที่จ่ายออกไป

มูลค่าปัจจุบันของชุดการชำระเงินในอนาคต

มูลค่าปัจจุบันคือจำนวนเงินทั้งหมดที่ชุดของการชำระเงินในอนาคตมีมูลค่าในขณะนี้ คุณสามารถคำนวณมูลค่าปัจจุบันโดยใช้ฟังก์ชัน Excel -

• PV- คำนวณมูลค่าปัจจุบันของการลงทุนโดยใช้อัตราดอกเบี้ยและชุดของการชำระเงินในอนาคต (มูลค่าติดลบ) และรายได้ (ค่าบวก) กระแสเงินสดอย่างน้อยหนึ่งรายการต้องเป็นบวกและอย่างน้อยก็ต้องเป็นลบ

• NPV - คำนวณมูลค่าปัจจุบันสุทธิของการลงทุนโดยใช้อัตราคิดลดและชุดของการชำระเงินในอนาคตเป็นงวด ๆ (มูลค่าติดลบ) และรายได้ (ค่าบวก)

• XNPV - คำนวณมูลค่าปัจจุบันสุทธิสำหรับตารางกระแสเงินสดที่ไม่จำเป็นต้องเป็นงวด

Note that -

• กระแสเงินสด PV ต้องคงที่ในขณะที่กระแสเงินสด NPV สามารถเปลี่ยนแปลงได้

• กระแสเงินสด PV สามารถเป็นได้ทั้งที่จุดเริ่มต้นหรือเมื่อสิ้นสุดรอบระยะเวลาในขณะที่กระแสเงินสด NPV จะต้องเป็นช่วงสิ้นงวด

• กระแสเงินสด NPV ต้องเป็นงวดในขณะที่กระแสเงินสด XNPV ไม่จำเป็นต้องเป็นงวด

ในส่วนนี้คุณจะเข้าใจวิธีการทำงานกับ PV คุณจะได้เรียนรู้เกี่ยวกับ NPV ในส่วนต่อไป

ตัวอย่าง

สมมติว่าคุณกำลังซื้อตู้เย็น พนักงานขายบอกคุณว่าราคาตู้เย็นคือ 32000 แต่คุณมีทางเลือกในการชำระเงินใน 8 ปีด้วยอัตราดอกเบี้ย 13% ต่อปีและจ่ายปีละ 6000 นอกจากนี้คุณยังมีตัวเลือกในการชำระเงิน ไม่ว่าจะในช่วงต้นหรือปลายปี

คุณต้องการทราบว่าตัวเลือกใดที่เป็นประโยชน์สำหรับคุณ

คุณสามารถใช้ฟังก์ชัน Excel PV -

PV (rate, nper, pmt, [fv ], [type])

ในการคำนวณมูลค่าปัจจุบันด้วยการชำระเงินทุกสิ้นปีให้ละเว้นประเภทหรือระบุ 0 สำหรับประเภท

ในการคำนวณมูลค่าปัจจุบันด้วยการชำระเงินทุกสิ้นปีให้ระบุ 1 สำหรับประเภท

คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

ดังนั้น,

• หากคุณชำระเงินตอนนี้คุณต้องจ่าย 32,000 ของมูลค่าปัจจุบัน
• หากคุณเลือกชำระเงินแบบรายปีพร้อมการชำระเงินเมื่อสิ้นปีคุณจะต้องจ่าย 28, 793 ของมูลค่าปัจจุบัน
• หากคุณเลือกชำระเงินแบบรายปีพร้อมการชำระเงินในช่วงสิ้นปีคุณจะต้องจ่าย 32,536 ของมูลค่าปัจจุบัน

คุณจะเห็นได้อย่างชัดเจนว่าตัวเลือกที่ 2 มีประโยชน์สำหรับคุณ

EMI คืออะไร?

การผ่อนชำระรายเดือนที่เท่าเทียมกัน (EMI) ถูกกำหนดโดย Investopedia ว่า "จำนวนเงินที่ผู้กู้คงจ่ายให้กับผู้ให้กู้ ณ วันที่กำหนดในแต่ละเดือนตามปฏิทินการผ่อนชำระต่อเดือนที่เท่ากันจะใช้เพื่อชำระทั้งดอกเบี้ยและเงินต้นในแต่ละเดือนเพื่อให้เกิน จำนวนปีที่ระบุเงินกู้จะชำระเต็มจำนวน "

EMI ในการกู้ยืม

ใน Excel คุณสามารถคำนวณ EMI จากการยืมด้วยฟังก์ชัน PMT

สมมติว่าคุณต้องการกู้สินเชื่อบ้านจำนวน 5000000 อัตราดอกเบี้ยต่อปี 11.5% และระยะเวลาเงินกู้ 25 ปี คุณสามารถค้นหา EMI ของคุณได้ดังนี้ -

• คำนวณอัตราดอกเบี้ยต่อเดือน (อัตราดอกเบี้ยต่อปี / 12)
• คำนวณจำนวนการชำระเงินต่อเดือน (จำนวนปี * 12)
• ใช้ฟังก์ชัน PMT เพื่อคำนวณ EMI

อย่างที่คุณสังเกต

• มูลค่าปัจจุบัน (PV) คือจำนวนเงินกู้
• มูลค่าในอนาคต (FV) คือ 0 เมื่อสิ้นสุดระยะเวลาจำนวนเงินกู้ควรเป็น 0
• ประเภทคือ 1 เนื่องจากมีการจ่าย EMI ทุกต้นเดือน

คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

การชำระเงินต้นและดอกเบี้ยรายเดือนจากเงินกู้

EMI รวมทั้งดอกเบี้ยและการชำระเงินต้นบางส่วน เมื่อเวลาเพิ่มขึ้นองค์ประกอบทั้งสองนี้ของ EMI จะแตกต่างกันไปทำให้สมดุลลดลง

ที่จะได้รับ

• ส่วนดอกเบี้ยของการชำระเงินรายเดือนของคุณคุณสามารถใช้ฟังก์ชัน Excel IPMT

• การชำระเงินส่วนหลักของการชำระเงินรายเดือนของคุณคุณสามารถใช้ฟังก์ชัน Excel PPMT

ตัวอย่างเช่นหากคุณกู้เงิน 1,000,000 เป็นระยะเวลา 8 เดือนในอัตรา 16% ต่อปี คุณสามารถรับค่าของ EMI จำนวนดอกเบี้ยที่ลดลงการชำระเงินต้นที่เพิ่มขึ้นและยอดเงินกู้ที่ลดลงในช่วง 8 เดือน เมื่อครบ 8 เดือนยอดเงินกู้จะเป็น 0

ทำตามขั้นตอนที่ระบุด้านล่าง

Step 1 - คำนวณ EMI ดังนี้

ส่งผลให้ EMI เป็น Rs 13261.59.

Step 2 - ถัดไปคำนวณดอกเบี้ยและส่วนเงินต้นของ EMI สำหรับ 8 เดือนตามที่แสดงด้านล่าง

คุณจะได้รับผลลัพธ์ดังต่อไปนี้

ดอกเบี้ยและเงินต้นที่จ่ายระหว่างสองช่วงเวลา

คุณสามารถคำนวณดอกเบี้ยและเงินต้นที่ชำระระหว่างสองช่วงเวลาได้

• คำนวณดอกเบี้ยสะสมจ่ายระหว่าง 2 ^{ครั้ง}และ 3 ^ถเดือนโดยใช้ฟังก์ชั่น CUMIPMT

• ตรวจสอบผลที่ได้ข้อสรุปถึงค่าดอกเบี้ย 2 ^{ครั้ง}และ 3 ^ถเดือน

• คำนวณเงินต้นสะสมที่จ่ายระหว่าง 2 ^{ครั้ง}และ 3 ^ถเดือนโดยใช้ฟังก์ชั่น CUMPRINC

• ตรวจสอบผลที่ได้ข้อสรุปถึงค่านิยมหลัก 2 ^{ครั้ง}และ 3 ^ถเดือน

คุณจะได้รับผลลัพธ์ดังต่อไปนี้

คุณจะเห็นว่าการคำนวณของคุณตรงกับผลการยืนยันของคุณ

การคำนวณอัตราดอกเบี้ย

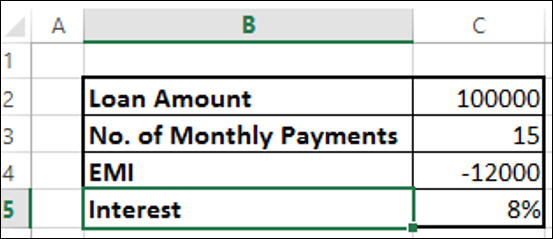
สมมติว่าคุณใช้เงินกู้ 100,000 และคุณต้องการคืนทุนใน 15 เดือนโดยมีการชำระเงินสูงสุดต่อเดือนที่ 12000 คุณอาจต้องการทราบอัตราดอกเบี้ยที่คุณต้องจ่าย

ค้นหาอัตราดอกเบี้ยด้วยฟังก์ชัน Excel RATE -

คุณจะได้ผลลัพธ์เป็น 8%

การคำนวณระยะเวลากู้ยืม

สมมติว่าคุณกู้เงิน 100,000 ในอัตราดอกเบี้ย 10% คุณต้องการผ่อนต่อเดือนสูงสุด 15,000 คุณอาจต้องการทราบว่าจะใช้เวลานานเท่าใดในการเคลียร์เงินกู้

ค้นหาจำนวนการชำระเงินด้วยฟังก์ชัน Excel NPER

คุณจะได้รับผลลัพธ์เป็น 12 เดือน

การตัดสินใจในการลงทุน

เมื่อคุณต้องการลงทุนให้เปรียบเทียบตัวเลือกต่างๆและเลือกตัวเลือกที่ให้ผลตอบแทนดีกว่า มูลค่าปัจจุบันสุทธิมีประโยชน์ในการเปรียบเทียบกระแสเงินสดในช่วงเวลาหนึ่งและตัดสินใจว่ากระแสใดดีกว่า กระแสเงินสดสามารถเกิดขึ้นในช่วงเวลาปกติเป็นงวดหรือในช่วงเวลาที่ไม่สม่ำเสมอ

อันดับแรกเราพิจารณากรณีของ regular, periodical cash flows.

มูลค่าปัจจุบันสุทธิของลำดับกระแสเงินสดที่ได้รับ ณ จุดต่างๆในช่วงเวลา n ปีนับจากนี้ (n สามารถเป็นเศษส่วนได้) คือ 1/(1 + r)ⁿโดยที่ r คืออัตราดอกเบี้ยรายปี

พิจารณาการลงทุนสองรายการต่อไปนี้ในช่วง 3 ปี

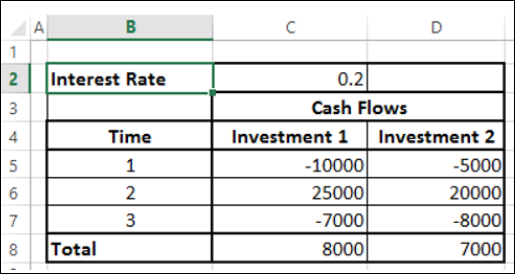
ด้วยมูลค่าที่ตราไว้การลงทุน 1 ดูดีกว่าการลงทุน 2 อย่างไรก็ตามคุณสามารถตัดสินใจได้ว่าจะลงทุนแบบใดดีกว่าก็ต่อเมื่อคุณทราบมูลค่าที่แท้จริงของการลงทุน ณ วันนี้ คุณสามารถใช้ฟังก์ชัน NPV เพื่อคำนวณผลตอบแทน

กระแสเงินสดสามารถเกิดขึ้นได้

• ในช่วงปลายปีของทุกปี
• ในช่วงต้นปีของทุกปี
• ในช่วงกลางปีของทุกปี

ฟังก์ชัน NPV จะถือว่ากระแสเงินสด ณ สิ้นปี หากกระแสเงินสดเกิดขึ้นในช่วงเวลาที่ต่างกันคุณต้องคำนึงถึงปัจจัยเฉพาะนั้นควบคู่ไปกับการคำนวณด้วย NPV

สมมติว่ากระแสเงินสดเกิดขึ้นในช่วงปลายปี จากนั้นคุณสามารถใช้ฟังก์ชัน NPV ได้ทันที

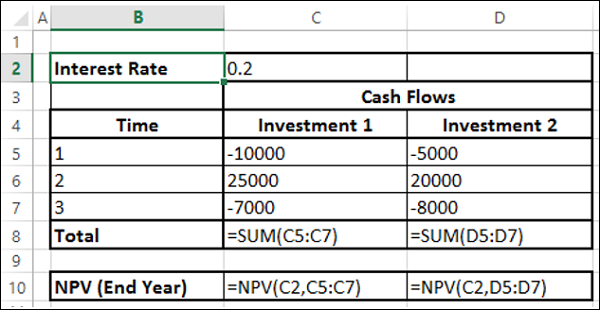
คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

ดังที่คุณสังเกต NPV สำหรับการลงทุน 2 สูงกว่าการลงทุน 1 ดังนั้นการลงทุน 2 จึงเป็นทางเลือกที่ดีกว่า คุณได้ผลลัพธ์นี้เนื่องจากกระแสเงินสดออกสำหรับการลงทุน 2 จะอยู่ในช่วงเวลาต่อมาเมื่อเทียบกับการลงทุน 1

กระแสเงินสดในช่วงต้นปี

สมมติว่ากระแสเงินสดเกิดขึ้นทุกต้นปี ในกรณีนี้คุณไม่ควรรวมกระแสเงินสดแรกในการคำนวณ NPV เนื่องจากเป็นมูลค่าปัจจุบันอยู่แล้ว คุณต้องเพิ่มกระแสเงินสดก้อนแรกให้กับ NPV ที่ได้รับจากกระแสเงินสดส่วนที่เหลือเพื่อให้ได้มูลค่าปัจจุบันสุทธิ

คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

กระแสเงินสดในช่วงกลางปี

สมมติว่ากระแสเงินสดเกิดขึ้นในช่วงกลางของทุกปี ในกรณีนี้คุณต้องคูณ NPV ที่ได้รับจากกระแสเงินสดด้วย $ \ sqrt {1 + r} $ เพื่อให้ได้มูลค่าปัจจุบันสุทธิ

คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

กระแสเงินสดในช่วงเวลาที่ไม่สม่ำเสมอ

หากคุณต้องการคำนวณมูลค่าปัจจุบันสุทธิด้วยกระแสเงินสดที่ผิดปกตินั่นคือกระแสเงินสดที่เกิดขึ้นในช่วงเวลาสุ่มการคำนวณจะค่อนข้างซับซ้อน

อย่างไรก็ตามใน Excel คุณสามารถคำนวณได้อย่างง่ายดายด้วยฟังก์ชัน XNPV

• จัดเรียงข้อมูลของคุณด้วยวันที่และกระแสเงินสด

Note- วันที่แรกในข้อมูลของคุณควรเป็นวันที่เร็วที่สุดของวันที่ทั้งหมด วันที่อื่น ๆ สามารถเกิดขึ้นในลำดับใดก็ได้

• ใช้ฟังก์ชัน XNPV เพื่อคำนวณมูลค่าปัจจุบันสุทธิ

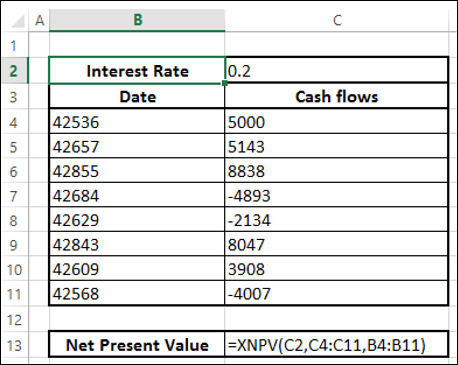
คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

วันที่สมมติว่าวันนี้คือ 15 ^THมีนาคม 2015 ในขณะที่คุณสังเกตทุกวันของกระแสเงินสดที่มีวันต่อมา หากคุณต้องการหามูลค่าปัจจุบันสุทธิ ณ วันนี้ให้รวมไว้ในข้อมูลที่ด้านบนและระบุ 0 สำหรับกระแสเงินสด

คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

อัตราผลตอบแทนภายใน (IRR)

อัตราผลตอบแทนภายใน (IRR) ของการลงทุนคืออัตราดอกเบี้ยที่ NPV เท่ากับ 0 เป็นค่าอัตราที่มูลค่าปัจจุบันของกระแสเงินสดที่เป็นบวกชดเชยค่าลบอย่างแน่นอน เมื่ออัตราคิดลดคือ IRR การลงทุนจะไม่แยแสอย่างสมบูรณ์กล่าวคือนักลงทุนจะไม่ได้รับหรือเสียเงิน

พิจารณากระแสเงินสดต่อไปนี้อัตราดอกเบี้ยที่แตกต่างกันและค่า NPV ที่สอดคล้องกัน

ดังที่คุณสามารถสังเกตได้ระหว่างค่าของอัตราดอกเบี้ย 10% และ 11% สัญญาณของ NPV จะเปลี่ยนไป เมื่อคุณปรับอัตราดอกเบี้ยเป็น 10.53% NPV เกือบเป็น 0 ดังนั้น IRR จึงเท่ากับ 10.53%

การกำหนด IRR ของกระแสเงินสดสำหรับโครงการ

คุณสามารถคำนวณ IRR ของกระแสเงินสดด้วยฟังก์ชัน Excel IRR

IRR เท่ากับ 10.53% ตามที่คุณเห็นในหัวข้อก่อนหน้านี้

สำหรับกระแสเงินสดที่กำหนด IRR อาจ -

• มีอยู่และไม่เหมือนใคร
• มีอยู่และหลายรายการ
• ไม่มีอยู่จริง

IRR ที่เป็นเอกลักษณ์

หากมี IRR และไม่เหมือนใครก็สามารถใช้เพื่อเลือกการลงทุนที่ดีที่สุดท่ามกลางความเป็นไปได้ต่างๆ

• หากกระแสเงินสดก้อนแรกเป็นลบหมายความว่านักลงทุนมีเงินและต้องการลงทุน จากนั้น IRR ที่สูงขึ้นก็จะยิ่งดีขึ้นเนื่องจากแสดงถึงอัตราดอกเบี้ยที่นักลงทุนได้รับ

• หากกระแสเงินสดแรกเป็นบวกหมายความว่านักลงทุนต้องการเงินและกำลังมองหาเงินกู้ยิ่ง IRR ต่ำเท่าไรก็ยิ่งดีขึ้นเท่านั้นเนื่องจากเป็นอัตราดอกเบี้ยที่นักลงทุนจ่าย

หากต้องการดูว่า IRR ไม่ซ้ำกันหรือไม่ให้เปลี่ยนค่าเดาและคำนวณ IRR ถ้า IRR คงที่แสดงว่าไม่ซ้ำกัน

ตามที่คุณสังเกต IRR มีค่าเฉพาะสำหรับค่าการเดาที่แตกต่างกัน

IRR หลายรายการ

ในบางกรณีคุณอาจมี IRR หลายตัว พิจารณากระแสเงินสดต่อไปนี้ คำนวณ IRR ด้วยค่าเดาที่แตกต่างกัน

คุณจะได้รับผลลัพธ์ดังต่อไปนี้ -

คุณสามารถสังเกตได้ว่ามี IRR สองตัว - -9.59% และ 216.09% คุณสามารถตรวจสอบ IRR ทั้งสองนี้คำนวณ NPV ได้

สำหรับทั้ง -9.59% และ 216.09% NPV คือ 0

ไม่มี IRR

ในบางกรณีคุณอาจไม่มี IRR พิจารณากระแสเงินสดต่อไปนี้ คำนวณ IRR ด้วยค่าเดาที่แตกต่างกัน

คุณจะได้ผลลัพธ์เป็น #NUM สำหรับค่าเดาทั้งหมด

ผลลัพธ์ #NUM หมายความว่าไม่มี IRR สำหรับกระแสเงินสดที่พิจารณา

รูปแบบกระแสเงินสดและ IRR

หากกระแสเงินสดมีการเปลี่ยนแปลงเพียงเครื่องหมายเดียวเช่นจากลบเป็นบวกหรือบวกเป็นลบจะมีการรับประกัน IRR ที่ไม่ซ้ำกัน ตัวอย่างเช่นในการลงทุนกระแสเงินสดแรกจะเป็นลบในขณะที่กระแสเงินสดที่เหลือจะเป็นบวก ในกรณีเช่นนี้จะมี IRR ที่ไม่ซ้ำกัน

หากกระแสเงินสดมีการเปลี่ยนแปลงมากกว่าหนึ่งสัญญาณอาจไม่มี IRR แม้ว่าจะมีอยู่จริง แต่ก็อาจไม่ซ้ำใคร

การตัดสินใจตาม IRR

นักวิเคราะห์หลายคนชอบใช้ IRR และเป็นตัววัดความสามารถในการทำกำไรที่ได้รับความนิยมเนื่องจากเป็นเปอร์เซ็นต์นั้นง่ายต่อการเข้าใจและเปรียบเทียบกับผลตอบแทนที่ต้องการ อย่างไรก็ตามมีปัญหาบางอย่างในระหว่างการตัดสินใจกับ IRR หากคุณจัดอันดับด้วย IRR และตัดสินใจตามอันดับเหล่านี้คุณอาจตัดสินใจผิดพลาด

คุณได้เห็นแล้วว่า NPV จะช่วยให้คุณสามารถตัดสินใจทางการเงินได้ อย่างไรก็ตาม IRR และ NPV จะไม่นำไปสู่การตัดสินใจแบบเดียวกันเสมอไปเมื่อโปรเจ็กต์ไม่รวมกัน

Mutually exclusive projectsเป็นโครงการที่การคัดเลือกโครงการหนึ่งขัดขวางการยอมรับอีกโครงการหนึ่ง เมื่อโปรเจ็กต์ที่กำลังถูกเปรียบเทียบไม่สามารถใช้ร่วมกันได้ความขัดแย้งในการจัดอันดับอาจเกิดขึ้นระหว่าง NPV และ IRR หากคุณต้องเลือกระหว่างโครงการ A และโครงการ B NPV อาจแนะนำให้ยอมรับโครงการ A ในขณะที่ IRR อาจแนะนำโครงการ B

ความขัดแย้งประเภทนี้ระหว่าง NPV และ IRR อาจเกิดขึ้นเนื่องจากสาเหตุต่อไปนี้ -

• โครงการมีขนาดแตกต่างกันมากหรือ
• ช่วงเวลาของกระแสเงินสดแตกต่างกัน

โครงการที่มีขนาดแตกต่างกันอย่างมีนัยสำคัญ

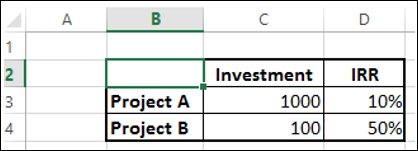
หากคุณต้องการตัดสินใจโดย IRR โครงการ A ให้ผลตอบแทน 100 และโครงการ B ผลตอบแทน 50 ดังนั้นการลงทุนในโครงการ A จึงมีผลกำไร อย่างไรก็ตามนี่เป็นการตัดสินใจที่ผิดเนื่องจากความแตกต่างในขนาดของโครงการ

พิจารณา -

• คุณมี 1,000 ที่จะลงทุน

• หากคุณลงทุนทั้งหมด 1,000 ในโครงการ A คุณจะได้รับผลตอบแทน 100

• หากคุณลงทุน 100 ในโครงการ B คุณจะยังมี 900 อยู่ในมือที่คุณสามารถลงทุนในโครงการอื่นได้เช่นพูดโครงการ C สมมติว่าคุณได้รับผลตอบแทน 20% จากโครงการ C จากนั้นผลตอบแทนทั้งหมดของโครงการ B และโครงการ C คือ 230 ซึ่งเป็นหนทางข้างหน้าในการทำกำไร

ดังนั้น NPV จึงเป็นวิธีที่ดีกว่าในการตัดสินใจในกรณีดังกล่าว

โครงการที่มีการกำหนดเวลากระแสเงินสดต่างกัน

อีกครั้งหากคุณพิจารณา IRR เพื่อตัดสินใจโครงการ B จะเป็นทางเลือก อย่างไรก็ตามโครงการ A มี NPV ที่สูงกว่าและเป็นทางเลือกที่เหมาะ

IRR ของกระแสเงินสดที่เว้นระยะไม่สม่ำเสมอ (XIRR)

กระแสเงินสดของคุณบางครั้งอาจมีระยะห่างไม่สม่ำเสมอ ในกรณีนี้คุณไม่สามารถใช้ IRR ได้เนื่องจาก IRR ต้องใช้ช่วงเวลาที่เว้นระยะเท่ากัน คุณสามารถใช้ XIRR แทนซึ่งคำนึงถึงวันที่ของกระแสเงินสดพร้อมกับกระแสเงินสด

อัตราผลตอบแทนภายในที่ได้คือ 26.42%

แก้ไข IRR (MIRR)

พิจารณากรณีที่อัตราทางการเงินของคุณแตกต่างจากอัตราการลงทุนซ้ำของคุณ หากคุณคำนวณอัตราผลตอบแทนภายในด้วย IRR จะถือว่าอัตราเดียวกันสำหรับทั้งการเงินและการลงทุนซ้ำ นอกจากนี้คุณอาจได้รับ IRR หลายรายการ

ตัวอย่างเช่นพิจารณากระแสเงินสดที่ระบุด้านล่าง -

ดังที่คุณสังเกต NPV เป็น 0 มากกว่าหนึ่งครั้งส่งผลให้มี IRR หลายตัว นอกจากนี้อัตราการลงทุนซ้ำจะไม่ถูกนำมาพิจารณา ในกรณีเช่นนี้คุณสามารถใช้แก้ไข IRR (MIRR) ได้

คุณจะได้รับผล 7% ตามที่แสดงด้านล่าง -

Note - ไม่เหมือนกับ IRR MIRR จะไม่ซ้ำกันเสมอ