Ağ Teorisi - Birleştirilmiş Devreler
Bir elektrik devresinin bir coupled circuit, o devrede bulunan bobinler (veya indüktörler) arasında karşılıklı bir endüktans olduğunda. Bobin, direnç ve indüktörün seri kombinasyonundan başka bir şey değildir. Direnç yokluğunda bobin indüktör olur. Bazen, bobin ve indüktör terimleri birbirinin yerine kullanılır.
Bu bölümde, önce nokta kuralını tartışalım ve sonra kuplaj sınıflandırmasını tartışalım.
Nokta Sözleşmesi
Nokta kuralı, noktalı terminaldeki voltaj polaritesi hakkında ayrıntılar veren bir tekniktir. Bu bilgi, KVL denklemlerini yazarken kullanışlıdır.
Akım bir bobinin (veya indüktörün) noktalı terminaline girerse, o zaman sahip olan başka bir bobinde (veya indüktörde) bir voltaj indükler. positive polarity noktalı terminalde.
Akım bir bobinin (veya indüktörün) noktalı terminalinden ayrılırsa, o zaman sahip olan başka bir bobinde (veya indüktörde) bir voltaj indükler. negative polarity noktalı terminalde.
Kaplinin Sınıflandırılması
Sınıflandırabiliriz coupling aşağıdaki iki kategoriye.
- Elektrik Bağlantısı
- Manyetik Kaplin
Şimdi, her bir bağlantı türünü tek tek tartışalım.
Elektrik Bağlantısı
Elektrik bağlantısı, bir physical connectioniki bobin (veya indüktör) arasında. Bu bağlantı, yardımcı tipte veya karşıt tipte olabilir. Akımın noktalı terminale mi girdiği yoksa noktalı terminalden mi çıktığına bağlıdır.
Aiding tipinin kuplajı
Birbirine bağlı iki indüktöre sahip olan aşağıdaki elektrik devresini düşünün. series.
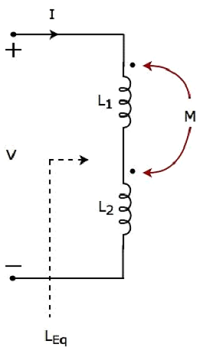
İki indüktör seri olarak bağlandığından, same current IL 1 ve L 2 öz endüktanslarına sahip her iki indüktörden akış .
Bu durumda, akım, her indüktörün noktalı terminaline giriyorum. Bu nedenle, her bir indüktördeki indüklenen voltaj,positive polarity başka bir bobinde akan akım nedeniyle noktalı terminalde.
Uygulamak KVL yukarıdaki elektrik devresinin veya ağın döngüsü etrafında.
$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$
$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$
$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$
Yukarıdaki denklem şu şekildedir: $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
bu yüzden equivalent inductance Yukarıdaki şekilde gösterilen indüktörlerin seri kombinasyonu
$$L_{Eq} = L_1 + L_2 + 2M$$
Bu durumda, eşdeğer endüktans 2M artırılmıştır. Bu nedenle, yukarıdaki elektrik devresi bir örnektir.electrical olan kaplin aiding yazın.
Karşıt tipte kaplin
Birbirine bağlı iki indüktöre sahip olan aşağıdaki elektrik devresini düşünün. series.
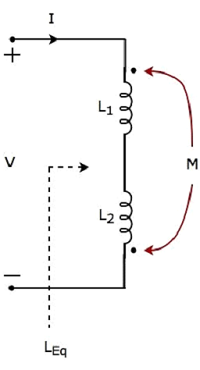
Yukarıdaki devrede, akım I endüktansa sahip indüktörün noktalı terminaline girer L1. Bu nedenle, diğer indüktörde endüktansa sahip bir voltaj indükler.L2. Yani,positive polarity Bu indüktörün noktalı terminalinde indüklenen voltajın% 50'si mevcuttur.
Yukarıdaki devrede, akım I indüktansa sahip olan indüktörün noktalı terminalinden yapraklar L2. Bu nedenle, diğer indüktörde endüktansa sahip bir voltaj indükler.L1. Yani,negative polarity Bu indüktörün noktalı terminalinde indüklenen voltajın% 50'si mevcuttur.
Uygulamak KVL yukarıdaki elektrik devresinin veya ağın döngüsü etrafında.
$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$
$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$
$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$
Yukarıdaki denklem şu şekildedir: $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
bu yüzden equivalent inductance Yukarıdaki şekilde gösterilen indüktörlerin seri kombinasyonu
$$L_{Eq} = L_1 + L_2 - 2M$$
Bu durumda, eşdeğer endüktans 2M azaltılmıştır. Bu nedenle, yukarıdaki elektrik devresi bir örnektir.electrical olan kaplin opposing yazın.
Manyetik Kaplin
Manyetik bağlantı olduğunda no physical connectioniki bobin (veya indüktör) arasında. Bu bağlantı, yardımcı tipte veya karşıt tipte olabilir. Akımın noktalı terminale mi girdiği yoksa noktalı terminalden mi çıktığına bağlıdır.
Aiding tipinin kuplajı
Aşağıdaki elektriksel eşdeğerini düşünün circuit of transformer. İki bobine sahip olup bunlara birincil ve ikincil bobinler denmektedir.
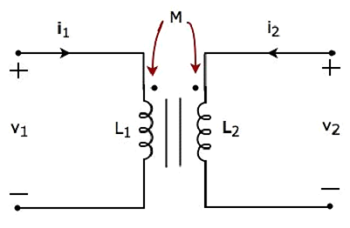
Birincil ve ikincil bobinlerden geçen akımlar sırasıyla i 1 ve i 2'dir . Bu durumda, bu akımlarenterilgili bobinin noktalı terminalinde. Bu nedenle, her bir bobindeki indüklenen voltaj, başka bir bobinde akan akım nedeniyle noktalı terminalde pozitif polariteye sahip olacaktır.
Uygulamak KVL birincil bobin etrafında.
$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$Equation 1
Uygulamak KVL ikincil bobin etrafında.
$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$Equation 2
Eşitlik 1 ve Denklem 2'de, kendinden indüklenen voltaj ve karşılıklı olarak indüklenen voltaj aynı polariteye sahiptir. Bu nedenle, yukarıdaki transformatör devresi bir örnektir.magnetic couplinghangisi aiding yazın.
Karşı Tip Kaplin
Aşağıdaki elektriksel eşdeğerini düşünün circuit of transformer.

Birincil ve ikincil bobinlerden geçen akımlar sırasıyla i 1 ve i 2'dir . Bu durumda, akım, i 1 birincil bobinin noktalı terminaline girer. Bu nedenle, ikincil bobinde bir voltaj oluşturur. Yani,positive polarity Endüklenen voltajın% 50'si bu ikincil bobinin noktalı terminalinde mevcuttur.
Yukarıdaki devrede, akım, i 2 sekonder bobinin noktalı terminalinden çıkar. Bu nedenle, birincil bobinde bir voltaj oluşturur. Yani,negative polarity Bu birincil bobinin noktalı terminalinde indüklenen voltajın% 50'si mevcuttur.
Uygulamak KVL birincil bobin etrafında.
$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$Equation 3
Uygulamak KVL ikincil bobin etrafında.
$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$Equation 4
Eşitlik 3 ve Denklem 4'te, kendinden indüklenen voltaj ve karşılıklı olarak indüklenen voltaj, zıt kutuplara sahiptir. Bu nedenle, yukarıdaki transformatör devresi bir örnektir.magnetic couplinghangisi opposing yazın.