Ağ Teorisi - Yıldızdan Üçgeye Dönüşüm
Önceki bölümde, delta ağının eşdeğer bir yıldız ağına dönüştürülmesinden bahsetmiştik. Şimdi, yıldız ağının eşdeğer bir delta ağına dönüştürülmesinden bahsedelim. Bu dönüşümeStar to Delta Conversion.
Önceki bölümde, resistances of star network delta ağından
$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ Equation 3
Yıldız Ağı Dirençleri Açısından Delta Ağ Dirençleri
Yıldız ağının dirençleri açısından delta ağının dirençlerini elde etmek için yukarıdaki denklemleri kullanalım.
Multiply her iki denklem seti ve sonra add.
$$ R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 ^ 2 R_3 + R_2 R_3 ^ 2 R_1 + R_3 R_1 ^ 2 R_2} {(R_1 + R_2 + R_3) ^ 2} $$
$$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3 (R_1 + R_2 + R_3)} {(R_1 + R_2 + R_3) ^ 2} $$
$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3} {R_1 + R_2 + R_3} $ Equation 4
Denklem 4'ü Denklem 2'ye bölerek,
$$ \ frac {R_A R_B + R_B R_C + R_C R_A} {R_B} = R_1 $$
$$ \ Rightarrow R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
Denklem 4'ü Denklem 3'e bölerek,
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
Denklem 4'ü Denklem 1'e bölerek,
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
Yukarıdaki ilişkileri kullanarak, yıldız ağının direnişlerinden delta ağının dirençlerini bulabiliriz. Bu şekilde dönüştürebilirizstar network into delta network.
Misal
Hesaplayalım resistances of delta network, aşağıdaki şekilde gösterildiği gibi yıldız ağına eşdeğerdir.
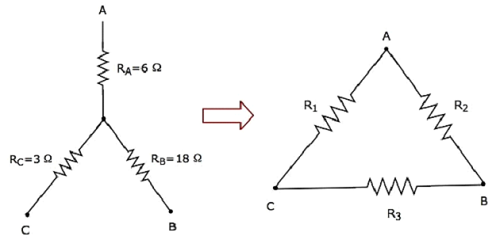
Verilen resistances of star networkolarak R bir = 6 Ω, R, B = 18 Ω ve R, Cı- = 3 Ω .
Aşağıdaki ilişkilerini biliyoruz resistances of delta network yıldız ağının dirençleri açısından.
$$ R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
Yukarıdaki denklemlerde R A , R B ve R C değerlerini değiştirin .
$$ R_1 = 3 + 6 + \ frac {3 \ times 6} {18} = 9 + 1 = 10 \ Omega $$
$$ R_2 = 6 + 18 + \ frac {6 \ times 18} {3} = 24 + 36 = 60 \ Omega $$
$$ R_3 = 18 + 3 + \ frac {18 \ times 3} {6} = 21 + 9 = 30 \ Omega $$
Yani, delta ağının dirençlerini aldık. R1 = 10 Ω, R2 = 60 Ω ve R3 = 30 Ω, verilen yıldız ağının dirençlerine eşdeğerdir.