Ağ Teorisi - Kirchhoff Kanunları
Ağ öğeleri aşağıdakilerden biri olabilir active veya passiveyazın. Herhangi bir elektrik devresi veya ağ, bu iki tür ağ elemanından birini veya her ikisinin bir kombinasyonunu içerir.
Şimdi, popüler olarak bilinen şu iki yasayı tartışalım: Kirchhoff’s laws.
- Kirchhoff'un Mevcut Yasası
- Kirchhoff'un Gerilim Yasası
Kirchhoff'un Mevcut Yasası
Kirchhoff'un Mevcut Yasası (KCL), bir düğümü terk eden (veya giren) akımların cebirsel toplamının sıfıra eşit olduğunu belirtir.
Bir Nodeiki veya daha fazla devre elemanının kendisine bağlı olduğu bir noktadır. Bir düğüme yalnızca iki devre elemanı bağlıysa, o zaman basit düğüm olduğu söylenir. Bir düğüme üç veya daha fazla devre elemanı bağlıysa, o zamanPrincipal Node.
MathematicallyKCL şu şekilde temsil edilebilir:
$$ \ displaystyle \ toplam \ limitler_ {m = 1} ^ M I_m = 0 $$
Nerede,
Imdüğümden çıkan m inci dal akımıdır.
M bir düğüme bağlı dalların sayısıdır.
Yukarıdaki ifade KCL"Bir düğüme giren akımların cebirsel toplamı, bir düğümü terk eden akımların cebirsel toplamına eşittir" olarak da ifade edilebilir. Bu ifadeyi aşağıdaki örnekle doğrulayalım.
Misal
Yazmak KCL equation düğümde P aşağıdaki şeklin.
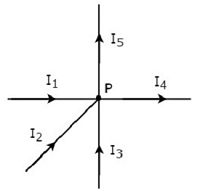
Yukarıdaki şekilde, dal akımlar I 1 , I 2 ve 3 vardırentering P düğümünde Bu üç akım için negatif işaretleri düşünün.
Yukarıdaki şekilde, şube akımlar I 4 ve ben 5 vardırleaving P düğümünden. Yani, bu iki akım için pozitif işaretleri düşünün.
KCL equation P düğümünde
$$ - I_1 - I_2 - I_3 + I_4 + I_5 = 0 $$
$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$
Yukarıdaki denklemde, sol taraf, giren akımların toplamını temsil ederken, sağ taraf, çıkış akımlarının toplamını temsil eder.
Bu eğiticide, akım bir düğümden çıktığında pozitif işareti ve bir düğüme girdiğinde negatif işareti ele alacağız. Benzer şekilde, akım bir düğümden çıktığında negatif işareti ve bir düğüme girdiğinde pozitif işareti düşünebilirsiniz. Her iki durumda daresult will be same.
Note - KCL, bir düğüme bağlı ağ öğelerinin doğasından bağımsızdır.
Kirchhoff'un Gerilim Yasası
Kirchhoff'un Gerilim Yasası (KVL), bir döngü veya ağ etrafındaki gerilimlerin cebirsel toplamının sıfıra eşit olduğunu belirtir.
Bir Loopbaşladığı aynı düğümde sona eren bir yoldur. Aksine, birMesh içinde başka herhangi bir döngü içermeyen bir döngüdür.
Matematiksel olarak KVL şu şekilde temsil edilebilir:
$$ \ displaystyle \ sum \ limits_ {n = 1} ^ N V_n = 0 $$
Nerede,
Vnn inci elemanın bir döngüdeki (ağ) voltajıdır.
N döngüdeki (ağ) ağ öğelerinin sayısıdır.
Yukarıdaki ifade KVL"Gerilim kaynaklarının cebirsel toplamı, bir döngüde mevcut olan gerilim düşüşlerinin cebirsel toplamına eşittir" olarak da ifade edilebilir. Bu ifadeyi aşağıdaki örnek yardımıyla doğrulayalım.
Misal
Yazmak KVL equation Aşağıdaki devrenin döngüsü etrafında.
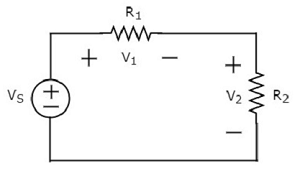
Yukarıdaki devre şeması, iki direnç R 1 ve R 2 ile seri olarak V S voltaj kaynağından oluşur . Dirençler R 1 ve R 2 üzerindeki voltaj düşüşleri sırasıyla V 1 ve V 2'dir .
Uygulamak KVL döngü etrafında.
$$ V_S - V_1 - V_2 = 0 $$
$$ \ Rightarrow V_S = V_1 + V_2 $$
Yukarıdaki denklemde, sol taraftaki terim tek voltaj kaynağı VS'yi temsil eder. Sağ taraf isesum of voltage drops. Bu örnekte, yalnızca bir voltaj kaynağını ele aldık. Bu nedenle sol taraf yalnızca bir terim içerir. Birden fazla voltaj kaynağı düşünürsek, sol taraf voltaj kaynaklarının toplamını içerir.
Bu eğitimde, her bir elemanın voltajının işaretini, döngü etrafında seyahat ederken mevcut olan ikinci terminalin polaritesi olarak ele alıyoruz. Benzer şekilde, her bir voltajın işaretini döngü etrafında seyahat ederken mevcut olan ilk terminalin polaritesi olarak düşünebilirsiniz. Her iki durumda daresult will be same.
Note - KVL, bir döngüde bulunan ağ öğelerinin doğasından bağımsızdır.