Ağ Teorisi - Düğüm Analizi
Herhangi bir elektrik şebekesini çözmek için kullanılan iki temel yöntem vardır: Nodal analysis ve Mesh analysis. Bu bölümde, konu hakkında tartışalım.Nodal analysis yöntem.
Düğüm analizinde, Düğüm gerilimlerini Toprağa göre ele alacağız. Bu nedenle, Düğüm analizi aynı zamandaNode-voltage method.
Düğüm Analizi Prosedürü
Nodal analizini kullanarak herhangi bir elektrik ağını veya devreyi çözerken bu adımları izleyin.
Step 1 - Tanımlayın principal nodes ve bunlardan birini seçin reference node. Bu referans düğümünü Zemin olarak ele alacağız.
Step 2 - Etiketle node voltages Referans düğüm hariç tüm ana düğümlerden Yere göre.
Step 3 - Yaz nodal equationsreferans düğümü hariç tüm ana düğümlerde. Düğüm denklemi, önce KCL ve ardından Ohm kanunu uygulanarak elde edilir.
Step 4 - Düğüm voltajlarını elde etmek için 3. Adımda elde edilen düğüm denklemlerini çözün.
Şimdi, düğüm voltajlarını kullanarak herhangi bir elemandan geçen akımı ve verilen ağda bulunan herhangi bir elemandaki voltajı bulabiliriz.
Misal
Aşağıdaki devrenin 20 Ω direncinden geçen akımı bulunuz. Nodal analysis.
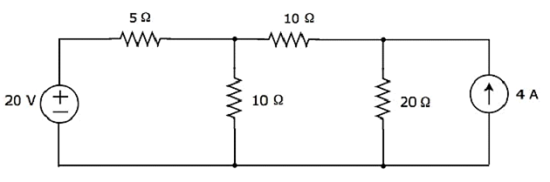
Step 1 - vardır three principle nodesyukarıdaki devrede. Bunlar aşağıdaki şekilde 1, 2 ve 3 olarak etiketlenmiştir.
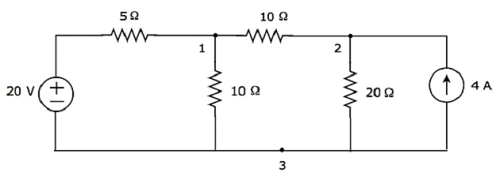
Yukarıdaki şekilde düşünün node 3 referans düğümü olarak (Zemin).
Step 2- Düğüm gerilimleri, V 1 ve V 2 , aşağıdaki şekilde etiketlenmiştir.
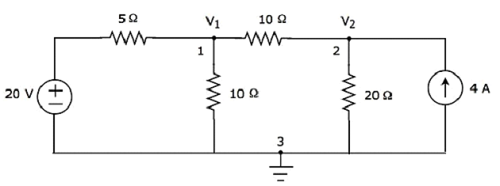
Yukarıdaki şekilde, V 1 zemine göre 1 düğümünde gerilim ve V 2 zemine göre düğüm 2'den gerilimdir.
Step 3 - Bu durumda alacağız two nodal equationsZeminden başka 1 ve 2 olmak üzere iki ana düğüm vardır. Düğüm denklemlerini bir düğüme yazdığımızda, akımın yönünün belirtilmediği düğümden tüm akımların ayrıldığını ve bu düğümün voltajının devredeki diğer düğüm voltajlarından daha büyük olduğunu varsayalım.
nodal equation 1. düğümde
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow \ frac {2 V_1 - 40 + V_1 + V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow 4V_1 - 40 - V_2 = 0 $$
$ \ Rightarrow V_2 = 4V_1 - 40 $ Equation 1
nodal equation 2. düğümde
$$ - 4 + \ frac {V_2} {20} + \ frac {V_2 - V_1} {10} = 0 $$
$$ \ Rightarrow \ frac {-80 + V_2 + 2V_2 - 2V_2} {20} = 0 $$
$ \ Rightarrow 3V_2 - 2V_1 = 80 $ Equation 2
Step 4- Denklem 1 ve Denklem 2'yi çözerek düğüm voltajlarını, V 1 ve V 2'yi bulmak .
Denklem 2'deki Yedek Denklem 1.
3 $$ (4 V_1 - 40) - 2 V_1 = 80 $$
$$ \ Rightarrow 12 V_1 - 120 - 2V_1 = 80 $$
$$ \ Rightarrow 10 V_1 = 200 $$
$$ \ Rightarrow V_1 = 20V $$
Yerine V 1 Equation1 içinde = 20 V.
$$ V_2 = 4 (20) - 40 $$
$$ \ Rightarrow V_2 = 40V $$
Yani, biz düğüm gerilimleri var V 1 ve V 2 olarak20 V ve 40 V sırasıyla.
Step 5- 20 Ω direnç üzerindeki voltaj, düğüm voltajı V 2'den başka bir şey değildir ve 40 V'a eşittir. Şimdi, Ohm yasasını kullanarak 20 Ω dirençten geçen akımı bulabiliriz.
$$ I_ {20 \ Omega} = \ frac {V_2} {R} $$
Yukarıdaki denklemde V 2 ve R değerlerini değiştirin .
$$ I_ {20 \ Omega} = \ frac {40} {20} $$
$$ \ Rightarrow I_ {20 \ Omega} = 2A $$
Bu nedenle, verilen devrenin 20 Ω direncinden geçen akım 2 A.
Note- Yukarıdaki örnekten, elektrik devresinde 'n' ana düğüm varsa (referans düğüm hariç) 'n' düğüm denklemlerini çözmemiz gerektiği sonucuna varabiliriz. Bu nedenle, Nodal analizini seçebiliriz.number of principal nodes (referans düğüm hariç) herhangi bir elektrik devresinin ağ sayısından daha azdır.