Ağ Teorisi - Paralel Rezonans
Önceki bölümde, dizi rezonansının önemini tartışmıştık. Şimdi, RLC devrelerindeki paralel rezonansı tartışalım.
Paralel Rezonans Devre Şeması
Rezonans paralel RLC devresinde meydana gelirse, o zaman denir Parallel Resonance. Aşağıdakileri göz önünde bulundurparallel RLC circuit, fazör alanında temsil edilir.
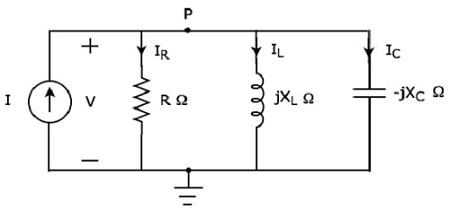
Burada direnç, indüktör ve kondansatör gibi pasif elemanlar paralel bağlanır. Bu kombinasyonun tamamıparallel giriş sinüzoidal akım kaynağı ile.
Yazmak nodal equation P düğümünde
$$ - I + I_R + I_L + I_C = 0 $$
$$ \ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$
$$ \ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup] $Equation 1
Yukarıdaki denklem şu şekildedir: I = VY.
bu yüzden admittance Y paralel RLC devresinin
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Rezonansta Parametreler ve Elektriksel Miktarlar
Şimdi, paralel RLC devresinin rezonansındaki parametrelerin ve elektriksel büyüklüklerin değerlerini tek tek türetelim.
Rezonans Frekansı
Biliyoruz ki resonant frequency, frrezonansın meydana geldiği frekanstır. Paralel RLC devresinde rezonans, hayali kabul terimi Y sıfır olduğunda meydana gelir. yani, $ \ frac {1} {X_C} - \ frac {1} {X_L} $ değeri sıfıra eşit olmalıdır
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ Rightarrow X_L = X_C $$
Yukarıdaki rezonans koşulu, seri RLC devresininki ile aynıdır. Böyleceresonant frequency, fr hem seri RLC devresinde hem de paralel RLC devresinde aynı olacaktır.
bu yüzden resonant frequency, fr paralel RLC devresinin
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
Nerede,
- L, bir indüktörün endüktansıdır.
- C, bir kapasitörün kapasitansıdır.
resonant frequency, fr paralel RLC devresinin sadece endüktansa bağlıdır L ve kapasite C. Ama direnişten bağımsızdırR.
Kabul
Biz var admittance Y paralel RLC devresinin
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Yukarıdaki denklemde, $ X_L = X_C $ yerine koyun.
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_C} \ rgroup $$
$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$
$$ \ Rightarrow Y = \ frac {1} {R} $$
Rezonansta, admittance, Paralel RLC devresinin Y'si, direncin tersine eşittir, R. yani $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $
Her Eleman boyunca voltaj
Denklem 1'deki $ \ frac {1} {X_C} - \ frac {1} {X_L} = 0 $ değiştirin
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ Rightarrow I = \ frac {V} {R} $$
$$ \ Rightarrow V = IR $$
bu yüzden voltage rezonanstaki paralel RLC devresinin tüm elemanları arasında V = IR.
Rezonansta, paralel RLC devresinin kabulü minimum değere ulaşır. Bu nedenlemaximum voltage rezonansta bu devrenin her bir elemanı boyunca bulunur.
Dirençten geçen akım
Dirençten geçen akım
$$ I_R = \ frac {V} {R} $$
Değerini değiştirin V yukarıdaki denklemde.
$$ I_R = \ frac {IR} {R} $$
$$ \ Rightarrow I_R = I $$
bu yüzden current flowing through resistor rezonansta $ \ mathbf {\ mathit {I_R = I}} $ 'dır.
İndüktörden geçen akım
İndüktörden geçen akım
$$ I_L = \ frac {V} {j X_L} $$
Değerini değiştirin V yukarıdaki denklemde.
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$
$$ \ Rightarrow I_L = -jQI $$
bu yüzden current flowing through inductor rezonansta $ I_L = -jQI $.
Böylece magnitude rezonansta indüktörden geçen akım
$$ | I_L | = QI $$
Nerede, Q Quality factor ve değeri $ \ frac {R} {X_L} $ 'a eşittir
Kondansatörden geçen akım
Kondansatörden geçen akım
$$ I_C = \ frac {V} {- j X_C} $$
Değerini değiştirin V yukarıdaki denklemde.
$$ I_C = \ frac {IR} {- j X_C} $$
$$ \ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I $$
$$ \ Rightarrow I_C = jQI $$
bu yüzden current flowing through capacitor rezonansta $ I_C = jQI $
Böylece magnitude rezonansta kapasitörden akan akımın
$$ | I_C | = QI $$
Nerede, Q Quality factor ve değeri $ \ frac {R} {X_C} $ 'a eşittir
Note - Paralel rezonans RLC devresi olarak adlandırılır current magnificationdevre. Çünkü, indüktör ve kondansatörden geçen akımın büyüklüğü , giriş sinüzoidal akım I'in Q katına eşittir .