Ağ Teorisi - AC Devrelerinin Tepkisi
Önceki bölümde, DC devresinin geçici yanıtı ve kararlı durum yanıtını tartıştık. Bu bölümde tartışalımresponse of AC circuit. Önceki bölümde tartıştığımız hem geçici yanıt hem de sabit durum yanıtı kavramları burada da yararlı olacaktır.
Seri RL Devresinin Yanıtını Bulmak
Aşağıdakileri göz önünde bulundur series RL circuit diyagram.

Yukarıdaki devrede, switch tutuldu openkadar t = 0 ile ve kapatıldığı t = 0 . Dolayısıyla, tepe gerilimi V m volt olan AC gerilim kaynağı , bu ana kadar seri RL devresine bağlanmaz. Bu nedenle, varno initial current indüktörden akar.
Devre şeması, switch içinde closed pozisyonu aşağıdaki şekilde gösterilmiştir.
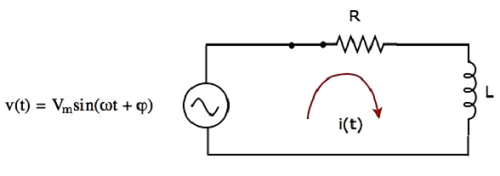
Şimdi, mevcut i (t) bir zirve voltajı olan AC gerilim kaynağı, çünkü, bütün devrede akar V m volt dizisi RL devresine bağlıdır.
Yukarıdaki devreden akan i (t) akımının iki terime sahip olacağını biliyoruz, biri geçici kısmı temsil eder ve diğer terim sabit durumu temsil eder.
Matematiksel olarak şu şekilde temsil edilebilir:
$i(t) = i_{Tr}(t) + i_{ss}(t)$Equation 1
Nerede,
$i_{Tr}(t)$ devreden geçen akımın geçici yanıtıdır.
$i_{ss}(t)$ devreden geçen akımın kararlı durum tepkisidir.
Önceki bölümde, seri RL devresinden geçen akımın geçici tepkisini aldık. Şeklindedir$Ke^{-\lgroup \frac{t}{\tau} \rgroup}$.
Vekil $i_{Tr}(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup}$ Denklem 1'de.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + i_{ss}(t)$Equation 2
Kararlı Durum Akımının Hesaplanması
Doğrusal elektrik devresine bir giriş olarak sinüzoidal bir sinyal uygulanırsa, o zaman aynı zamanda bir sabit durum çıkışı olan bir sabit durum çıkışı üretir. sinusoidal signal. Hem giriş hem de çıkış sinüzoidal sinyaller aynı frekansa, ancak farklı genliklere ve faz açılarına sahip olacaktır.
Sinüzoidal bir voltaj kaynağı tarafından uyarıldığında, bir elektrik devresinin kararlı durum yanıtını kullanarak hesaplayabiliriz. Laplace Transform approach.
S-alanı devre şeması, switch içinde closed pozisyonu aşağıdaki şekilde gösterilmiştir.
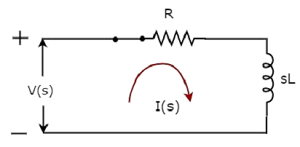
Yukarıdaki devrede, tüm miktarlar ve parametreler şu şekilde gösterilir: s-domain. Bunlar, zaman alanı miktarları ve parametrelerinin Laplace dönüşümleridir.
Transfer function yukarıdaki devrenin
$$H(s) = \frac{I(s)}{V(s)}$$
$$\Rightarrow H(s) = \frac{1}{Z(s)}$$
$$\Rightarrow H(s) = \frac{1}{R + sL}$$
Vekil $s = j \omega$ yukarıdaki denklemde.
$$H(j \omega) = \frac{1}{R + j \omega L}$$
Magnitude of $\mathbf{\mathit{H(j \omega)}}$ dır-dir
$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2}L^2}$$
Phase angle of $\mathbf{\mathit{H(j \omega)}}$ dır-dir
$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} \rgroup$$
Alacağız steady state current $i_{ss}(t)$ aşağıdaki iki adımı uygulayarak -
Giriş sinüzoidal voltajın tepe voltajını ve büyüklüğünü çarpın. $H(j \omega)$.
Giriş sinüzoidal voltajın faz açılarını ekleyin ve $H(j \omega)$.
steady state current $i_{ss}(t)$ olacak
$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Değerini değiştirin $i_{ss}(t)$ Denklem 2'de.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 3
Devrede başlangıç akımı olmadığını biliyoruz. Bu nedenle, sabitin değerini bulmak için Denklem 3'te t = 0 & i (t) = 0 koyun.
$$0 = Ke^{-\lgroup \frac{0}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Denklem 3'teki K değerini değiştirin .
$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup e^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 4
Denklem 4, sinüzoidal bir voltaj kaynağı tarafından uyarıldığında seri RL devresinden akan akımı temsil eder. İki şartı var. Birinci ve ikinci terimler sırasıyla akımın geçici yanıtı ve sabit durum yanıtını temsil eder.
Yapabiliriz neglect the first termDenklem 4'ün değeri birden çok daha az olacağı için. Böylece, devreden geçen sonuçta ortaya çıkan akım
$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Sadece içerir steady state term. Bu nedenle, AC devrelerinin yalnızca sabit durum yanıtını bulabilir ve bunun geçici yanıtını ihmal edebiliriz.