Ağ Teorisi - Pasif Öğeler
Bu bölümde Direnç, İndüktör ve Kondansatör gibi pasif unsurları detaylı olarak tartışacağız. Dirençler ile başlayalım.
Direnç
Direncin temel işlevi, elektrik akımının akışına karşıdır veya onu kısıtlar. Bu nedenle dirençler, akım akışı miktarını ve / veya bölme (paylaşım) voltajını sınırlamak için kullanılır.
Dirençten akan akımın ben amper olmasına ve üzerindeki voltajın V volt olmasına izin verin. symbol akım, I ve voltaj ile birlikte direnç, V aşağıdaki şekilde gösterilmektedir.
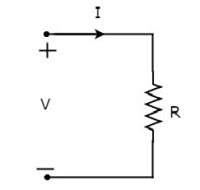
Göre Ohm’s law, direnç üzerindeki voltaj, içinden geçen akımın ve bu direncin direncinin ürünüdür. Mathematicallyşu şekilde temsil edilebilir:
$ V = IR $ Equation 1
$ \ Rightarrow I = \ frac {V} {R} $Equation 2
Nerede, R bir direncin direncidir.
Denklem 2'den, dirençten geçen akımın direnç boyunca uygulanan voltajla doğru orantılı olduğu ve direncin direnci ile ters orantılı olduğu sonucuna varabiliriz.
Power bir elektrik devresi elemanında şu şekilde temsil edilebilir:
$ P = VI $Equation 3
İkame, Denklem 3'teki Denklem 1.
$ P = (IR) I $
$ \ Rightarrow P = I ^ 2 R $ Equation 4
İkame, Denklem 3'teki Denklem 2.
$ P = V \ lgrup \ frac {V} {R} \ rgrup $
$ \ Rightarrow P = \ frac {V ^ 2} {R} $ Equation 5
Dolayısıyla, Denklem 3 ila 5'te belirtilen formüllerden birini kullanarak dirençte harcanan güç miktarını hesaplayabiliriz.
Bobin
Genel olarak, indüktörlerin dönüş sayısı olacaktır. Bu nedenle, içinden akım geçtiğinde manyetik akı üretirler. Dolayısıyla, bir indüktör tarafından üretilen toplam manyetik akı miktarı, içinden akan akıma bağlıdır ve bunların doğrusal bir ilişkisi vardır.
Mathematicallyşu şekilde yazılabilir
$$ \ Psi \: \ alpha \: I $$
$$ \ Rightarrow \ Psi = LI $$
Nerede,
Ψ toplam manyetik akıdır
L bir indüktörün endüktansıdır
İndüktörden akan akımın ben amper olmasına ve üzerindeki voltajın V volt olmasına izin verin . symbolAkım I ve voltaj V ile birlikte indüktörün değeri aşağıdaki şekilde gösterilmiştir.
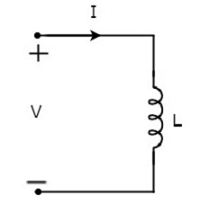
Göre Faraday’s law, indüktör üzerindeki voltaj şu şekilde yazılabilir:
$$ V = \ frac {d \ Psi} {dt} $$
Yerine V = LI yukarıdaki denklemde.
$$ V = \ frac {d (LI)} {dt} $$
$$ \ Rightarrow V = L \ frac {dI} {dt} $$
$$ \ Rightarrow I = \ frac {1} {L} \ int V dt $$
Yukarıdaki denklemlerden şu sonuca varabiliriz: linear relationship indüktör üzerindeki voltaj ile içinden geçen akım arasında.
Biz biliyoruz ki power bir elektrik devresi elemanında şu şekilde temsil edilebilir:
$$ P = VI $$
Yukarıdaki denklemde $ V = L \ frac {dI} {dt} $ yerine koyun.
$$ P = \ lgroup L \ frac {dI} {dt} \ rgroup I $$
$$ \ Rightarrow P = LI \ frac {dI} {dt} $$
Yukarıdaki denklemi entegre ederek elde edeceğiz energy bir indüktörde saklanır
$$ W = \ frac {1} {2} LI ^ 2 $$
Böylece, indüktör enerjiyi manyetik alan formunda depolar.
Kondansatör
Genel olarak, bir kapasitör, bir dielektrik ortam ile ayrılmış iki iletken plakaya sahiptir. Kondansatöre pozitif voltaj uygulanırsa, pozitif yük depolar. Benzer şekilde, kapasitör boyunca negatif voltaj uygulanırsa, negatif yük depolar.
Dolayısıyla, kondansatörde depolanan şarj miktarı uygulanan gerilime bağlıdır. Vkarşısında ve doğrusal bir ilişkileri var. Matematiksel olarak şu şekilde yazılabilir:
$$ Q \: \ alpha \: V $$
$$ \ Rightarrow Q = CV $$
Nerede,
Q kapasitörde depolanan yüktür.
C bir kapasitörün kapasitansıdır.
Kondansatörden akan akımın ben amper olmasına ve üzerindeki voltajın V volt olmasına izin verin . Akım I ve voltaj V ile birlikte kondansatör sembolü aşağıdaki şekilde gösterilmiştir.
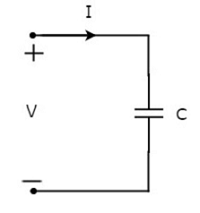
Biliyoruz ki current başka bir şey değil time rate of flow of charge. Matematiksel olarak şu şekilde temsil edilebilir:
$$ I = \ frac {dQ} {dt} $$
Yukarıdaki denklemde $ Q = CV $ yerine koyun.
$$ I = \ frac {d (CV)} {dt} $$
$$ \ Rightarrow I = C \ frac {dV} {dt} $$
$$ \ Rightarrow V = \ frac {1} {C} \ int I dt $$
Yukarıdaki denklemlerden şu sonuca varabiliriz: linear relationship kapasitördeki voltaj ile içinden geçen akım arasında.
Biz biliyoruz ki power bir elektrik devresi elemanında şu şekilde temsil edilebilir:
$$ P = VI $$
Yukarıdaki denklemde $ I = C \ frac {dV} {dt} $ yerine koyun.
$$ P = V \ lgroup C \ frac {dV} {dt} \ rgroup $$
$$ \ Rightarrow P = CV \ frac {dV} {dt} $$
Yukarıdaki denklemi entegre ederek elde edeceğiz energy kapasitörde saklandığı gibi
$$ W = \ frac {1} {2} CV ^ 2 $$
Böylece kondansatör, enerjiyi elektrik alanı şeklinde depolar.