Ağ Teorisi - DC Devrelerinin Tepkisi
Bir giriş için bir elektrik devresinin çıkışı zamana göre değişiklik gösteriyorsa, o zaman time response. Zaman cevabı aşağıdaki iki bölümden oluşur.
- Geçici tepki
- Kararlı durum tepkisi
Bu bölümde, önce bu iki yanıtı tartışalım ve ardından bir DC voltaj kaynağı tarafından uyarıldığında seri bir RL devresindeki bu iki yanıtı gözlemleyelim.
Geçici tepki
Bir elektrik devresine bir giriş uyguladıktan sonra, çıkışın sabit duruma ulaşması belirli bir zaman alır. Böylece, sabit bir duruma geçene kadar çıkış geçici durumda olacaktır. Bu nedenle, geçici durum sırasında elektrik devresinin tepkisi olarak bilinir.transient response.
Büyük 't' değerleri için geçici yanıt sıfır olacaktır. İdeal olarak, bu 't' değeri sonsuz olmalıdır. Ama pratik olarakfive time constants yeterlidir.
Geçici Akımların Varlığı veya Yokluğu
Şu nedenlerle yanıtta geçici olaylar meydana gelir: sudden changeelektrik devresine uygulanan kaynaklarda ve / veya anahtarlama eylemi nedeniyle. İki olası anahtarlama eylemi vardır. Bunlar açma anahtarı ve kapama anahtarıdır.
transient Bölüm olacak not presentsadece dirençler içeriyorsa, bir elektrik devresinin veya ağın cevabında. Çünküresistor herhangi bir miktarda voltaj ve akımı ayarlayabilme yeteneğine sahiptir.
transient part occurs enerji depolayan elemanların varlığı nedeniyle bir elektrik devresinin veya ağın tepkisinde inductor and capacitor. Çünkü bu elementlerde depolanan enerjiyi anında değiştiremezler.
İndüktör Davranışı
Anahtarlama eyleminin t = 0'da gerçekleştiğini varsayın .Inductor currentanahtarlama eylemi gerçekleştiğinde anında değişmez. Bu, anahtarlama eyleminden hemen sonraki indüktör akımının değerinin, anahtarlama eyleminden hemen öncekiyle aynı olacağı anlamına gelir.
Matematiksel olarak şu şekilde temsil edilebilir:
$$ i_L (0 ^ +) = i_L (0 ^ -) $$
Kondansatör Davranışı
capacitor voltageanahtarlama eylemi gerçekleştiğinde, indüktör akımına benzer şekilde anında değişmez. Bu, anahtarlama eyleminden hemen sonraki kapasitör voltajının değerinin, anahtarlama eyleminden hemen öncekiyle aynı olacağı anlamına gelir.
Matematiksel olarak şu şekilde temsil edilebilir:
$$ v_c (0 ^ +) = v_c (0 ^ -) $$
Kararlı durum tepkisi
Büyük 't' değerleri için geçici yanıt sıfır değer olduktan sonra bile kalan zaman yanıtının parçası olarak bilinir. steady state response. Bu, kararlı durum sırasında yanıtta herhangi bir geçici parça olmayacağı anlamına gelir.
İndüktör Davranışı
Bağımsız kaynak, uzun bir süre boyunca bir veya daha fazla indüktöre ve dirence (isteğe bağlı) sahip olan elektrik devresine veya ağa bağlanırsa, bu elektrik devresinin veya ağın sabit durumda olduğu söylenir. Bu nedenle, o elektrik devresinin indüktör (ler) inde depolanan enerji maksimum ve sabittir.
Matematiksel olarak şu şekilde temsil edilebilir:
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Maksimum ve sabit
$ \ Rightarrow i_L = $ Maksimum ve sabit
Bu nedenle, indüktör bir constant current source sabit durumda.
İndüktördeki voltaj
$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$
Böylece, indüktör bir short circuit sabit durumda.
Kondansatör Davranışı
Bağımsız kaynak, uzun bir süre boyunca bir veya daha fazla kapasitör ve direnci (isteğe bağlı) olan elektrik devresine veya ağa bağlanırsa, bu elektrik devresinin veya ağın sabit durumda olduğu söylenir. Bu nedenle, o elektrik devresinin kapasitör (ler) inde depolanan enerji maksimum ve sabittir.
Matematiksel olarak şu şekilde temsil edilebilir:
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Maksimum ve sabit
$ \ Rightarrow v_c = $ Maksimum ve sabit
Bu nedenle, kapasitör bir constant voltage source sabit durumda.
Kondansatörden geçen akım
$$ i_c = C \ frac {dv_c} {dt} = 0A $$
Yani, kapasitör bir open circuit sabit durumda.
Seri RL Devresinin Yanıtını Bulmak
Aşağıdakileri göz önünde bulundur series RL circuit diyagram.
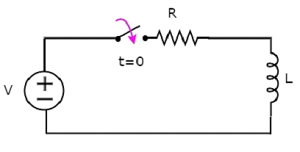
Yukarıdaki devrede, switch tutuldu opent = 0'a kadar ve t = 0'da kapatıldı. Dolayısıyla, V volt olan DC gerilim kaynağı bu ana kadar seri RL devresine bağlı değildir. Bu nedenle, varno initial current indüktörden akar.
Devre şeması, switch içinde closed pozisyon aşağıdaki şekilde gösterilmiştir.
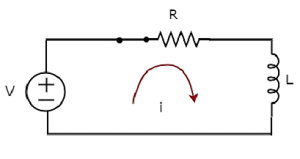
Şimdi, şimdiki i DC voltaj kaynağı sahip olduğu için tüm devrede akar V volt seri RL devresine bağlanır.
Şimdi başvur KVL döngü etrafında.
$$ V = Ri + L \ frac {di} {dt} $$
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
Yukarıdaki denklem birinci dereceden bir diferansiyel denklemdir ve şu şekildedir:
$ \ frac {dy} {dt} + Py = Q $Equation 2
Tarafından comparing Denklem 1 ve Denklem 2, aşağıdaki ilişkileri alacağız.
$$ x = t $$
$$ y = i $$
$$ P = \ frac {R} {L} $$
$$ Q = \ frac {V} {L} $$
solution Denklem 2'nin
$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
Nerede, k sabittir.
Denklem 3'teki x, y, P ve Q değerlerini değiştirin.
$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow yani ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $
$ \ Rightarrow yani ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
Devrede başlangıç akımı olmadığını biliyoruz. Dolayısıyla, ikame, t = 0 ve Sabitin değerini bulmak için Denklem 4'te = 0 k.
$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$
$$ 0 = \ frac {V} {R} + k (1) $$
$$ k = - \ frac {V} {R} $$
İkame, Denklem 4'teki k değeri.
$$ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
bu yüzden current devreden akan
$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
Dolayısıyla, seri RL devresinin yanıtı, bir DC voltaj kaynağı tarafından uyarıldığında, aşağıdaki iki terime sahiptir.
İlk $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ terimi şuna karşılık gelir: transient response.
İkinci terim $ \ frac {V} {R} $, steady state response. Bu iki yanıt aşağıdaki şekilde gösterilmektedir.
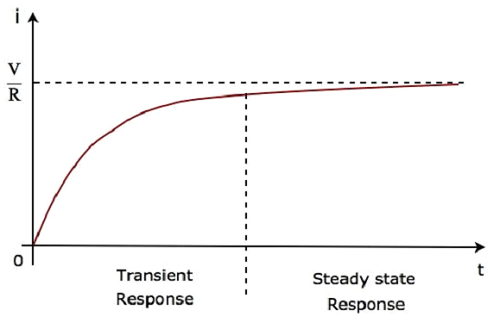
Denklem 5'i aşağıdaki gibi yeniden yazabiliriz -
$ i = \ frac {V} {R} \ lgrup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $
$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6
Nerede, τ ... time constant ve değeri $ \ frac {L} {R} $ 'a eşittir.
Denklem 5 ve Denklem 6 aynıdır. Ancak, birkaç değeri değiştirerek Denklem 6'dan devreden geçen akımın yukarıdaki dalga biçimini kolayca anlayabiliriz.t 0, τ, 2τ, 5τ vb. gibi
Devreden geçen akımın yukarıdaki dalga formunda, geçici yanıt sıfırdan beşe kadar zaman sabiti sunarken, kararlı durum yanıtı beş zaman sabitinden itibaren mevcut olacaktır.