Estadística: teorema del límite central
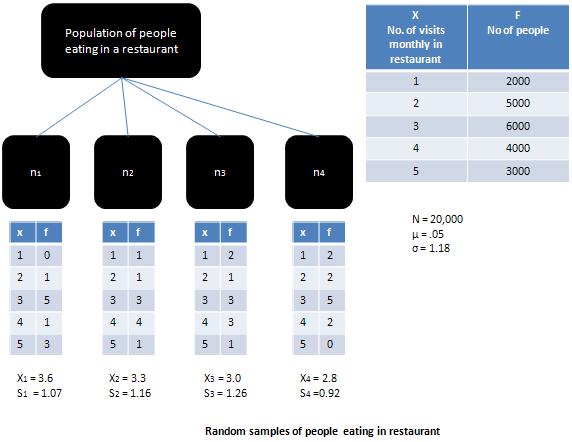
Si la población de la que se ha extraído la muestra es una población normal, entonces la sample means sería igual a la media de la población y la sampling distributionsería normal. Cuando la población está más sesgada, como es el caso ilustrado en la Figura, entonces lasampling distribution tendería a acercarse a la distribución normal, siempre que la muestra sea grande (es decir, mayor de 30).
De acuerdo a Central Limit Theorem, para muestras suficientemente grandes con un tamaño superior a 30, la forma del sampling distribution se volverá cada vez más como un normal distribution, independientemente de la forma de la población parental. Este teorema explica la relación entre elpopulation distribution y sampling distribution. Destaca el hecho de que si hay un conjunto de muestras suficientemente grande,sampling distribution de enfoques medios normal distribution. Richard ha resumido la importancia del teorema del límite central. I. Levin en las siguientes palabras:
La importancia del teorema del límite central radica en el hecho de que nos permite usar estadísticas muestrales para hacer inferencias sobre los parámetros de la población sin saber nada sobre la forma de la distribución de frecuencias de esa población que no sea lo que podemos obtener de la muestra.