Estadísticas - Análisis de residuos

El análisis de residuos se utiliza para evaluar la idoneidad de un modelo de regresión lineal mediante la definición de residuos y el examen de los gráficos de gráficos de residuos.

Residual

Residual ($ e $) se refiere a la diferencia entre el valor observado ($ y $) y el valor predicho ($ \ hat y $). Cada punto de datos tiene un residuo.

Parcela residual

Un gráfico de residuos es un gráfico en el que los residuos están en el eje vertical y la variable independiente está en el eje horizontal. Si los puntos se dispersan aleatoriamente alrededor del eje horizontal, entonces un modelo de regresión lineal es apropiado para los datos; de lo contrario, elija un modelo no lineal.

Tipos de parcela residual

El siguiente ejemplo muestra algunos patrones en los gráficos de residuos.

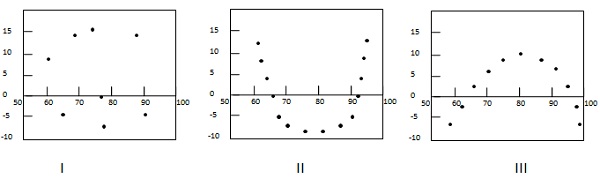
En el primer caso, los puntos se dispersan al azar. Por tanto, se prefiere el modelo de regresión lineal. En el segundo y tercer caso, los puntos no están dispersos al azar y sugieren que se prefiere un método de regresión no lineal.

Ejemplo

Problem Statement:

Compruebe dónde es apropiado un modelo de regresión lineal para los siguientes datos.

$ x $	60	70	80	85	95
$ y $ (valor real)	70	sesenta y cinco	70	95	85
$ \ hat y $ (valor previsto)	65.411	71.849	78.288	81.507	87.945

Solution:

Step 1: Calcule los residuos para cada punto de datos.

$ x $	60	70	80	85	95
$ y $ (valor real)	70	sesenta y cinco	70	95	85
$ \ hat y $ (valor previsto)	65.411	71.849	78.288	81.507	87.945
$ e $ (residual)	4.589	-6.849	-8.288	13.493	-2,945

Step 2: - Dibujar el gráfico de la parcela residual.

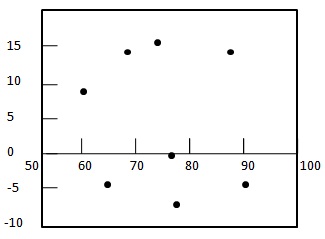
Step 3: - Verificar la aleatoriedad de los residuales.

Aquí el gráfico de residuos muestra un patrón aleatorio: el primer residuo es positivo, los dos siguientes son negativos, el cuarto es positivo y el último residual es negativo. Dado que el patrón es bastante aleatorio, lo que indica que un modelo de regresión lineal es apropiado para los datos anteriores.