Systemy sterowania - algebra diagramów blokowych

Algebra schematu blokowego to nic innego jak algebra związana z podstawowymi elementami schematu blokowego. Ta algebra zajmuje się obrazowym przedstawieniem równań algebraicznych.

Podstawowe połączenia dla bloków

Istnieją trzy podstawowe typy połączeń między dwoma blokami.

Połączenie szeregowe

Nazywa się również połączenie szeregowe cascade connection. Na poniższym rysunku dwa bloki posiadające funkcje transferu $ G_1 (s) $ i $ G_2 (s) $ są połączone szeregowo.

Dla tej kombinacji otrzymamy wynik $ Y (s) $ as

$$ Y (s) = G_2 (s) Z (s) $$

Gdzie $ Z (s) = G_1 (s) X (s) $

$$ \ Rightarrow Y (s) = G_2 (s) [G_1 (s) X (s)] = G_1 (s) G_2 (s) X (s) $$

$$ \ Rightarrow Y (s) = \ lbrace G_1 (s) G_2 (s) \ rbrace X (s) $$

Porównaj to równanie ze standardową postacią równania wyjściowego, $ Y (s) = G (s) X (s) $. Gdzie, $ G (s) = G_1 (s) G_2 (s) $.

Oznacza to, że możemy reprezentować series connectiondwóch bloków z jednym blokiem. Funkcja przenoszenia tego pojedynczego bloku toproduct of the transfer functionsz tych dwóch bloków. Równoważny schemat blokowy pokazano poniżej.

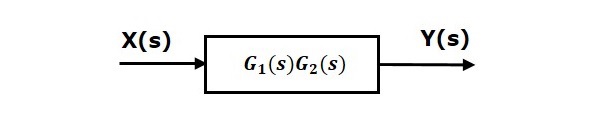
Podobnie można przedstawić szeregowe połączenie „n” bloków z pojedynczym blokiem. Funkcja przenoszenia tego pojedynczego bloku jest iloczynem funkcji przenoszenia wszystkich tych „n” bloków.

Połączenie równoległe

Bloki, które są połączone parallel będzie mieć same input. Na poniższym rysunku dwa bloki posiadające funkcje transferu $ G_1 (s) $ i $ G_2 (s) $ są połączone równolegle. Wyjścia tych dwóch bloków są połączone z punktem sumowania.

Dla tej kombinacji otrzymamy wynik $ Y (s) $ as

$$ Y (s) = Y_1 (s) + Y_2 (s) $$

Gdzie, $ Y_1 (s) = G_1 (s) X (s) $ i $ Y_2 (s) = G_2 (s) X (s) $

$$ \ Rightarrow Y (s) = G_1 (s) X (s) + G_2 (s) X (s) = \ lbrace G_1 (s) + G_2 (s) \ rbrace X (s) $$

Porównaj to równanie ze standardową postacią równania wyjściowego, $ Y (s) = G (s) X (s) $.

Gdzie, $ G (s) = G_1 (s) + G_2 (s) $.

Oznacza to, że możemy reprezentować parallel connectiondwóch bloków z jednym blokiem. Funkcja przenoszenia tego pojedynczego bloku tosum of the transfer functionsz tych dwóch bloków. Równoważny schemat blokowy pokazano poniżej.

Podobnie można przedstawić równoległe połączenie „n” bloków z pojedynczym blokiem. Funkcja przenoszenia tego pojedynczego bloku jest algebraiczną sumą funkcji transferu wszystkich tych „n” bloków.

Połączenie zwrotne

Jak omówiliśmy w poprzednich rozdziałach, istnieją dwa typy plików feedback- pozytywne opinie i negatywne opinie. Poniższy rysunek przedstawia system kontroli ujemnego sprzężenia zwrotnego. Tutaj dwa bloki posiadające funkcje transferu $ G (s) $ i $ H (s) $ tworzą zamkniętą pętlę.

Wynik punktu sumowania to -

$$ E (s) = X (s) -H (s) Y (s) $$

Wynik $ Y (s) $ wynosi -

$$ Y (s) = E (s) G (s) $$

Podstaw $ E (s) $ wartość w powyższym równaniu.

$$ Y (s) = \ left \ {X (s) -H (s) Y (s) \ rbrace G (s) \ right \} $$

$$ Y (s) \ left \ {1 + G (s) H (s) \ rbrace = X (s) G (s) \ right \} $$

$$ \ Rightarrow \ frac {Y (s)} {X (s)} = \ frac {G (s)} {1 + G (s) H (s)} $$

Dlatego funkcja przesyłania w zamkniętej pętli z ujemnym sprzężeniem zwrotnym to $ \ frac {G (s)} {1 + G (s) H (s)} $

Oznacza to, że możemy przedstawić połączenie ujemnego sprzężenia zwrotnego dwóch bloków za pomocą jednego bloku. Funkcja przenoszenia tego pojedynczego bloku jest funkcją przesyłania w pętli zamkniętej ujemnego sprzężenia zwrotnego. Równoważny schemat blokowy pokazano poniżej.

Podobnie można przedstawić połączenie dodatniego sprzężenia zwrotnego dwóch bloków w jednym bloku. Funkcja przenoszenia tego pojedynczego bloku jest funkcją przenoszenia w zamkniętej pętli dodatniego sprzężenia zwrotnego, tj. $ \ Frac {G (s)} {1-G (s) H (s)} $

Algebra diagramów blokowych dla punktów sumowania

Istnieją dwie możliwości przesuwania punktów sumowania względem bloków -

Przesunięcie punktu sumowania po bloku
Przesunięcie punktu sumowania przed blokiem

Zobaczmy teraz, jakie ustalenia należy poczynić kolejno w dwóch powyższych przypadkach.

Przesunięcie punktu podsumowania po bloku

Rozważ schemat blokowy pokazany na poniższym rysunku. Tutaj punkt sumowania znajduje się przed blokiem.

Punkt sumowania ma dwa wejścia $ R (s) $ i $ X (s) $. Wynik to $ \ left \ {R (s) + X (s) \ right \} $.

Zatem wejście do bloku $ G (s) $ to $ \ left \ {R (s) + X (s) \ right \} $, a wynikiem tego jest -

$$ Y (s) = G (s) \ left \ {R (s) + X (s) \ right \} $$

$ \ Rightarrow Y (s) = G (s) R (s) + G (s) X (s) $ (Equation 1)

Teraz przesuń punkt sumowania po bloku. Ten schemat blokowy pokazano na poniższym rysunku.

Wyjście bloku $ G (s) $ to $ G (s) R (s) $.

Wynik punktu sumowania to

$ Y (s) = G (s) R (s) + X (s) $ (Equation 2)

Porównaj równanie 1 i równanie 2.

Pierwszy wyraz $ 'G (s) R (s)' $ jest taki sam w obu równaniach. Ale jest różnica w drugiej kadencji. Aby drugi człon również był taki sam, potrzebujemy jeszcze jednego bloku $ G (s) $. Ma wejście $ X (s) $, a wyjście tego bloku jest podawane jako wejście do punktu sumowania zamiast $ X (s) $. Ten schemat blokowy pokazano na poniższym rysunku.

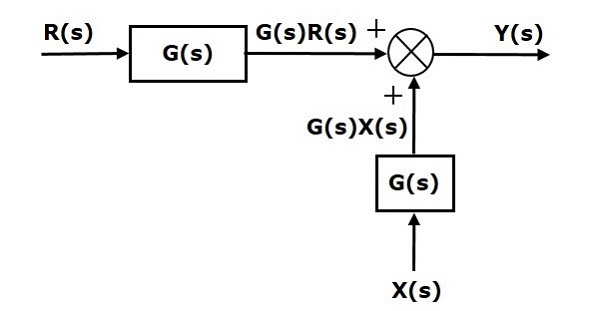
Przesunięcie punktu podsumowania przed blokiem

Rozważ schemat blokowy pokazany na poniższym rysunku. Tutaj punkt sumowania znajduje się po bloku.

Wyjście tego schematu blokowego to -

$ Y (s) = G (s) R (s) + X (s) $ (Equation 3)

Teraz przesuń punkt sumowania przed blokiem. Ten schemat blokowy pokazano na poniższym rysunku.

Wyjście tego schematu blokowego to -

$ Y (S) = G (s) R (s) + G (s) X (s) $ (Equation 4)

Porównaj równanie 3 i równanie 4,

Pierwszy wyraz $ 'G (s) R (s)' $ jest taki sam w obu równaniach. Ale jest różnica w drugiej kadencji. Aby drugi człon również był taki sam, potrzebujemy jeszcze jednego bloku $ \ frac {1} {G (s)} $. Ma wejście $ X (s) $, a wyjście tego bloku jest podawane jako wejście do punktu sumowania zamiast $ X (s) $. Ten schemat blokowy pokazano na poniższym rysunku.

Algebra diagramów blokowych dla punktów startu

Istnieją dwie możliwości przesuwania punktów startu względem bloków -

Przesunięcie punktu startu po bloku
Przesunięcie punktu startu przed blokiem

Zobaczmy teraz, jakie ustalenia należy poczynić w dwóch powyższych przypadkach, jeden po drugim.

Przesuwanie punktu startu za blokiem

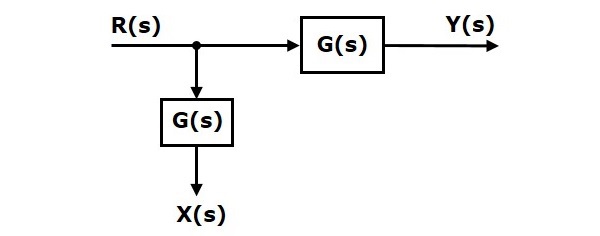
Rozważ schemat blokowy pokazany na poniższym rysunku. W tym przypadku punkt startu znajduje się przed blokiem.

Tutaj $ X (s) = R (s) $ i $ Y (s) = G (s) R (s) $

Kiedy przesuniesz punkt startu za blokiem, wyjście $ Y (s) $ będzie takie samo. Ale jest różnica w wartości X (s) $. Tak więc, aby uzyskać tę samą wartość $ X (s) $, potrzebujemy jeszcze jednego bloku $ \ frac {1} {G (s)} $. Ma wejście $ Y (s) $, a wyjście to $ X (s) $. Ten schemat blokowy pokazano na poniższym rysunku.

Przesuwanie punktu startu przed blokiem

Rozważ schemat blokowy pokazany na poniższym rysunku. Tutaj punkt startu znajduje się za blokiem.

Tutaj $ X (s) = Y (s) = G (s) R (s) $

Kiedy przesuniesz punkt startu przed blokiem, wyjście $ Y (s) $ będzie takie samo. Ale jest różnica w wartości X (s) $. Tak więc, aby uzyskać tę samą wartość $ X (s) $, potrzebujemy jeszcze jednego bloku $ G (s) $. Ma wejście $ R (s) $, a wyjście to $ X (s) $. Ten schemat blokowy pokazano na poniższym rysunku.