Odpowiedź systemu pierwszego rzędu
W tym rozdziale omówimy reakcję czasową systemu pierwszego rzędu. Rozważ poniższy schemat blokowy systemu sterowania w pętli zamkniętej. Tutaj funkcja przesyłania w otwartej pętli, $ \ frac {1} {sT} $ jest połączona z ujemnym sprzężeniem zwrotnym równym jedności.

Wiemy, że funkcja transferu systemu sterowania w pętli zamkniętej ma jedność ujemną sprzężenie zwrotne,
$$ \ frac {C (s)} {R (s)} = \ frac {G (s)} {1 + G (s)} $$
Zastąp $ G (s) = \ frac {1} {sT} $ w powyższym równaniu.
$$ \ frac {C (s)} {R (s)} = \ frac {\ frac {1} {sT}} {1+ \ frac {1} {sT}} = \ frac {1} {sT + 1} $$
W mianowniku potęga s jest jedna. W związku z tym powyższa funkcja transferu jest pierwszego rzędu i mówi się, że system jestfirst order system.
Możemy przepisać powyższe równanie jako
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $$
Gdzie,
C(s) jest transformatą Laplace'a sygnału wyjściowego c (t),
R(s) jest transformatą Laplace'a sygnału wejściowego r (t) i
T jest stałą czasową.
Wykonaj poniższe czynności, aby uzyskać odpowiedź (wynik) systemu pierwszego rzędu w dziedzinie czasu.
Weź transformatę Laplace'a sygnału wejściowego $ r (t) $.
Rozważmy równanie, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Zastąp $ R (s) $ wartość w powyższym równaniu.
W razie potrzeby wykonaj częściowe ułamki $ C (s) $.
Zastosuj odwrotną transformatę Laplace'a do $ C (s) $.
W poprzednim rozdziale widzieliśmy standardowe sygnały testowe, takie jak impuls, krok, rampa i parabolika. Znajdźmy teraz odpowiedzi systemu pierwszego rzędu dla każdego wejścia, jeden po drugim. Nazwa odpowiedzi jest podawana zgodnie z nazwą sygnału wejściowego. Na przykład odpowiedź systemu na wejście impulsowe nazywana jest odpowiedzią impulsową.
Odpowiedź impulsowa systemu pierwszego rzędu
Weź pod uwagę unit impulse signal jako dane wejściowe do systemu pierwszego rzędu.
Tak więc $ r (t) = \ delta (t) $
Zastosuj transformatę Laplace'a po obu stronach.
$ R (s) = 1 $
Rozważmy równanie, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Zastąp $ R (s) = 1 $ w powyższym równaniu.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) (1) = \ frac {1} {sT + 1} $$
Zmień układ powyższego równania na jedną ze standardowych form transformacji Laplace'a.
$$ C (s) = \ frac {1} {T \ left (\ s + \ frac {1} {T} \ right)} \ Rightarrow C (s) = \ frac {1} {T} \ left (\ frac {1} {s + \ frac {1} {T}} \ right) $$
Zastosuj odwrotną transformatę Laplace'a po obu stronach.
$$ c (t) = \ frac {1} {T} e ^ \ left ({- \ frac {t} {T}} \ right) u (t) $$
Na poniższym rysunku przedstawiono odpowiedź impulsową jednostki.
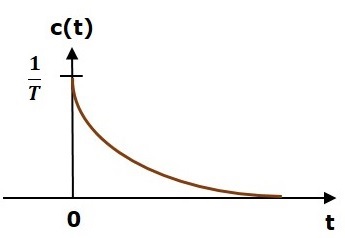
Plik unit impulse response, c (t) jest wykładniczo zanikającym sygnałem dla dodatnich wartości „t” i wynosi zero dla ujemnych wartości „t”.
Odpowiedź krokowa systemu pierwszego rzędu
Weź pod uwagę unit step signal jako wejście do systemu pierwszego rzędu.
A więc $ r (t) = u (t) $
Zastosuj transformatę Laplace'a po obu stronach.
$$ R (s) = \ frac {1} {s} $$
Rozważmy równanie, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Zastąp $ R (s) = \ frac {1} {s} $ w powyższym równaniu.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s} \ right) = \ frac {1} {s \ left (sT + 1 \ right)} $$
Wykonaj częściowe ułamki C (s).
$$ C (s) = \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1} $$
$$ \ Rightarrow \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A \ left (sT + 1 \ right) + Bs} {s \ left (sT + 1 \ right)} $$
Po obu stronach termin mianownik jest taki sam. Więc zostaną przez siebie anulowane. Dlatego zrównaj warunki licznika.
$$ 1 = A \ left (sT + 1 \ right) + Bs $$
Zrównując stałe wyrazy po obu stronach, otrzymasz A = 1.
Podstaw, A = 1 i zrównaj współczynnik s warunki po obu stronach.
$$ 0 = T + B \ Rightarrow B = -T $$
Podstawienie, A = 1 i B = −T w częściowej ekspansji ułamkowej $ C (s) $.
$$ C (s) = \ frac {1} {s} - \ frac {T} {sT + 1} = \ frac {1} {s} - \ frac {T} {T \ left (s + \ frac { 1} {T} \ right)} $$
$$ \ Rightarrow C (s) = \ frac {1} {s} - \ frac {1} {s + \ frac {1} {T}} $$
Zastosuj odwrotną transformatę Laplace'a po obu stronach.
$$ c (t) = \ left (1-e ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t) $$
Plik unit step response, c (t) ma zarówno stan przejściowy, jak i stan ustalony.
Przejściowy składnik w jednostkowej odpowiedzi skokowej to -
$$ c_ {tr} (t) = - e ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
Stan ustalony w jednostkowej odpowiedzi skokowej to -
$$ c_ {ss} (t) = u (t) $$
Poniższy rysunek przedstawia odpowiedź skokową jednostki.

Wartość unit step response, c(t)wynosi zero w chwili t = 0 i dla wszystkich ujemnych wartości t. Stopniowo rośnie od wartości zerowej i ostatecznie osiąga jeden w stanie ustalonym. Zatem wartość stanu ustalonego zależy od wielkości wejścia.
Odpowiedź rampowa systemu pierwszego rzędu
Weź pod uwagę unit ramp signal jako dane wejściowe do systemu pierwszego rzędu.
$ Więc r (t) = tu (t) $
Zastosuj transformatę Laplace'a po obu stronach.
$$ R (s) = \ frac {1} {s ^ 2} $$
Rozważmy równanie, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Zastąp $ R (s) = \ frac {1} {s ^ 2} $ w powyższym równaniu.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 2} \ right) = \ frac {1} {s ^ 2 ( sT + 1)} $$
Wykonaj częściowe ułamki $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A} {s ^ 2} + \ frac {B} {s} + \ frac {C} {sT +1} $$
$$ \ Rightarrow \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A (sT + 1) + Bs (sT + 1) + Cs ^ 2} {s ^ 2 (sT + 1) } $$
Po obu stronach termin mianownik jest taki sam. Więc zostaną przez siebie anulowane. Dlatego zrównaj warunki licznika.
$$ 1 = A (sT + 1) + Bs (sT + 1) + Cs ^ 2 $$
Zrównując stałe wyrazy po obu stronach, otrzymasz A = 1.
Zastąp, A = 1 i zrównaj współczynnik s składników po obu stronach.
$$ 0 = T + B \ Rightarrow B = -T $$
Podobnie, podstaw B = −T i zrównaj współczynnik $ s ^ 2 $ wyrażeń po obu stronach. Otrzymasz $ C = T ^ 2 $.
Podstawmy A = 1, B = −T i $ C = T ^ 2 $ w częściowej ekspansji ułamkowej $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {sT + 1} = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {T \ left (s + \ frac {1} {T} \ right)} $$
$$ \ Rightarrow C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}} $$
Zastosuj odwrotną transformatę Laplace'a po obu stronach.
$$ c (t) = \ left (t-T + Te ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t) $$
Plik unit ramp response, c (t) ma zarówno stan przejściowy, jak i stan ustalony.
Przejściowy termin w odpowiedzi jednostkowej rampy to -
$$ c_ {tr} (t) = Te ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
Stan ustalony w odpowiedzi jednostkowej rampy to -
$$ c_ {ss} (t) = (tT) u (t) $$
Poniższy rysunek przedstawia reakcję rampy jednostki.

Plik unit ramp response, c (t) następuje po jednostkowym sygnale wejściowym rampy dla wszystkich dodatnich wartości t. Ale istnieje odchylenie jednostek T od sygnału wejściowego.
Odpowiedź paraboliczna systemu pierwszego rzędu
Weź pod uwagę unit parabolic signal jako dane wejściowe do systemu pierwszego rzędu.
Więc $ r (t) = \ frac {t ^ 2} {2} u (t) $
Zastosuj transformatę Laplace'a po obu stronach.
$$ R (s) = \ frac {1} {s ^ 3} $$
Rozważmy równanie, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Podstaw $ R (s) = \ frac {1} {s ^ 3} $ w powyższym równaniu.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 3} \ right) = \ frac {1} {s ^ 3 ( sT + 1)} $$
Wykonaj częściowe ułamki $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 3 (sT + 1)} = \ frac {A} {s ^ 3} + \ frac {B} {s ^ 2} + \ frac {C} {s} + \ frac {D} {sT + 1} $$
Po uproszczeniu otrzymasz wartości A, B, C i D odpowiednio 1, $ -T, \: T ^ 2 \: i \: −T ^ 3 $. Zastąp te wartości w powyższej częściowej ekspansji C (s).
$ C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 3} {sT + 1 } \: \ Rightarrow C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 2} {s + \ frac {1} {T}} $
Zastosuj odwrotną transformatę Laplace'a po obu stronach.
$$ c (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} \ right ) u (t) $$
Plik unit parabolic response, c (t) ma zarówno stan przejściowy, jak i stan ustalony.
Przejściowy termin w jednostkowej odpowiedzi parabolicznej to
$$ C_ {tr} (t) = - T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
Określenie stanu ustalonego w jednostkowej odpowiedzi parabolicznej to
$$ C_ {ss} (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2 \ right) u (t) $$
Na podstawie tych odpowiedzi możemy wywnioskować, że systemy sterowania pierwszego rzędu nie są stabilne przy rampie i wejściach parabolicznych, ponieważ te odpowiedzi rosną nawet w nieskończonym czasie. Systemy sterowania pierwszego rzędu są stabilne z wejściami impulsowymi i krokowymi, ponieważ te odpowiedzi mają ograniczone wyjście. Ale odpowiedź impulsowa nie ma terminu stanu ustalonego. Tak więc sygnał kroku jest szeroko stosowany w dziedzinie czasu do analizowania systemów sterowania na podstawie ich odpowiedzi.