Systemy sterowania - wykresy Bode
Wykres Bodego lub diagram Bodego składa się z dwóch wykresów -
- Wykres wielkości
- Wykres fazowy
Na obu wykresach oś x przedstawia częstotliwość kątową (skala logarytmiczna). Natomiast oś y reprezentuje wielkość (skalę liniową) funkcji przenoszenia w otwartej pętli na wykresie wielkości i kąt fazowy (skala liniowa) funkcji przenoszenia w otwartej pętli na wykresie fazowym.
Plik magnitude funkcji przesyłania w otwartej pętli w dB wynosi -
$$ M = 20 \: \ log | G (j \ omega) H (j \ omega) | $$
Plik phase angle funkcji przenoszenia w otwartej pętli w stopniach wynosi -
$$ \ phi = \ angle G (j \ omega) H (j \ omega) $$
Note - Podstawa logarytmu wynosi 10.
Podstawy wykresów Bodego
Poniższa tabela pokazuje nachylenie, wielkość i wartości kąta fazowego składników występujących w funkcji przenoszenia w otwartej pętli. Te dane są przydatne podczas rysowania wykresów Bode.
| Rodzaj terminu | G (jω) H (jω) | Nachylenie (dB / dec) | Wielkość (dB) | Kąt fazowy (stopnie) |
|---|---|---|---|---|
Stały |
$ K $ |
0 $ |
20 $ \ log K $ |
0 $ |
Zero na początku |
$ j \ omega $ |
20 $ |
20 $ \ log \ omega $ |
90 $ |
'n' zer na początku |
$ (j \ omega) ^ n $ |
20 $ \: n $ |
20 $ \: n \ log \ omega $ |
90 $ \: n $ |
Polak na początku |
$ \ frac {1} {j \ omega} $ |
-20 $ |
-20 $ \ log \ omega $ |
-90 $ \: lub \: 270 $ |
'n' biegunów na początku |
$ \ frac {1} {(j \ omega) ^ n} $ |
-20 $ \: n $ |
-20 $ \: n \ log \ omega $ |
$ -90 \: n \: lub \: 270 \: n $ |
Proste zero |
$ 1 + j \ omega r $ |
20 $ |
$ 0 \: for \: \ omega <\ frac {1} {r} $ 20 $ \: \ log \ omega r \: for \: \ omega> \ frac {1} {r} $ |
$ 0 \: for \: \ omega <\ frac {1} {r} $ 90 $ \: za \: \ omega> \ frac {1} {r} $ |
Prosty słupek |
$ \ frac {1} {1 + j \ omega r} $ |
-20 $ |
$ 0 \: for \: \ omega <\ frac {1} {r} $ -20 $ \: \ log \ omega r \: for \: \ omega> \ frac {1} {r} $ |
$ 0 \: for \: \ omega <\ frac {1} {r} $ -90 $ \: lub \: 270 \: dla \: \ omega> \ frac {1} {r} $ |
Termin pochodny drugiego rzędu |
$ \ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right) $ |
40 $ |
40 $ \: \ log \: \ omega_n \: for \: \ omega <\ omega_n $ 20 $ \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: for \: \ omega = \ omega_n $ 40 $ \: \ log \: \ omega \: dla \: \ omega> \ omega_n $ |
$ 0 \: dla \: \ omega <\ omega_n $ 90 $ \: za \: \ omega = \ omega_n $ 180 $ \: za \: \ omega> \ omega_n $ |
Człon całkowy drugiego rzędu |
$ \ frac {1} {\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)} $ |
-40 $ |
$ -40 \: \ log \: \ omega_n \: for \: \ omega <\ omega_n $ -20 $ \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: dla \: \ omega = \ omega_n $ $ -40 \: \ log \: \ omega \: for \: \ omega> \ omega_n $ |
$ -0 \: dla \: \ omega <\ omega_n $ -90 $ \: dla \: \ omega = \ omega_n $ -180 $ \: dla \: \ omega> \ omega_n $ |
Rozważmy funkcję przesyłania w otwartej pętli $ G (s) H (s) = K $.
Wielkość $ M = 20 \: \ log K $ dB
Kąt fazowy $ \ phi = 0 $ stopni
Jeśli $ K = 1 $, wtedy wielkość wynosi 0 dB.
Jeśli $ K> 1 $, wtedy wielkość będzie dodatnia.
Jeśli $ K <1 $, wtedy wielkość będzie ujemna.
Poniższy rysunek przedstawia odpowiedni wykres Bodego.


Wykres wielkości jest linią poziomą niezależną od częstotliwości. Sama linia 0 dB jest wykresem wielkości, gdy wartość K wynosi jeden. W przypadku dodatnich wartości K linia pozioma przesunie się o 20 $ \: \ log K $ dB powyżej linii 0 dB. W przypadku ujemnych wartości K linia pozioma przesunie się o 20 $ \: \ log K $ dB poniżej linii 0 dB. Sama linia Zero stopni jest wykresem fazowym dla wszystkich dodatnich wartości K.
Rozważmy funkcję przesyłania w otwartej pętli $ G (s) H (s) = s $.
Wielkość $ M = 20 \ log \ omega $ dB
Kąt fazowy $ \ phi = 90 ^ 0 $
Przy $ \ omega = 0,1 $ rad / s, wielkość ta wynosi -20 dB.
Przy $ \ omega = 1 $ rad / s, wielkość wynosi 0 dB.
Przy $ \ omega = 10 $ rad / s, wielkość wynosi 20 dB.
Poniższy rysunek przedstawia odpowiedni wykres Bodego.


Wykres wielkości to linia o nachyleniu 20 dB / dec. Linia ta zaczynała się od $ \ omega = 0,1 $ rad / s i miała wielkość -20 dB i biegnie dalej na tym samym zboczu. Dotyka linii 0 dB przy $ \ omega = 1 $ rad / s. W tym przypadku wykres fazowy to 90 0 linii.
Rozważmy funkcję przenoszenia w otwartej pętli $ G (s) H (s) = 1 + s \ tau $.
Wielkość $ M = 20 \: log \ sqrt {1 + \ omega ^ 2 \ tau ^ 2} $ dB
Kąt fazowy $ \ phi = \ tan ^ {- 1} \ omega \ tau $ stopni
Dla $ ω <\ frac {1} {\ tau} $, wielkość wynosi 0 dB, a kąt fazowy wynosi 0 stopni.
Dla $ \ omega> \ frac {1} {\ tau} $, wielkość wynosi 20 $ \: \ log \ omega \ tau $ dB, a kąt fazowy wynosi 90 0 .
Poniższy rysunek przedstawia odpowiedni wykres Bodego.

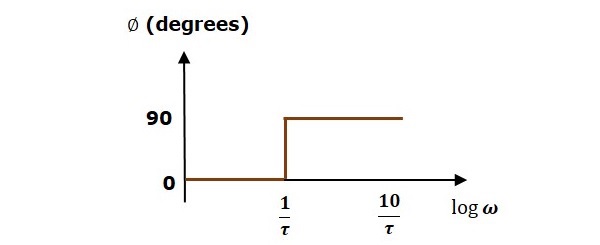
Wykres wielkości ma amplitudę od 0 dB do $ \ omega = \ frac {1} {\ tau} $ rad / s. Od $ \ omega = \ frac {1} {\ tau} $ rad / s, ma nachylenie 20 dB / dec. W tym przypadku wykres fazowy ma kąt fazowy od 0 stopni do $ \ omega = \ frac {1} {\ tau} $ rad / s, a stąd kąt fazowy wynosi 90 0 . Ten wykres Bodego nazywa sięasymptotic Bode plot.
Ponieważ wykresy wielkości i fazy są przedstawiane liniami prostymi, wykresy Dokładnego Bode przypominają asymptotyczne wykresy Bode. Jedyną różnicą jest to, że wykresy Exact Bode będą miały proste krzywe zamiast prostych.
Podobnie, możesz narysować wykresy Bode'a dla innych warunków funkcji przenoszenia w otwartej pętli, które są podane w tabeli.