Modelowanie układów mechanicznych
W tym rozdziale omówimy differential equation modelingukładów mechanicznych. Istnieją dwa rodzaje systemów mechanicznych opartych na typie ruchu.
- Translacyjne systemy mechaniczne
- Obrotowe układy mechaniczne
Modelowanie translacyjnych układów mechanicznych
Translacyjne systemy mechaniczne poruszają się wzdłuż a straight line. Systemy te składają się głównie z trzech podstawowych elementów. Są to masa, sprężyna i dashpot lub amortyzator.
Jeśli siła jest przyłożona do translacyjnego układu mechanicznego, przeciwstawia się jej przeciwstawne siły wynikające z masy, elastyczności i tarcia układu. Ponieważ przyłożona siła i przeciwstawne siły są w przeciwnych kierunkach, algebraiczna suma sił działających na układ wynosi zero. Spójrzmy teraz indywidualnie na siłę, której przeciwstawiają się te trzy elementy.
Masa
Masa jest własnością ciała, które przechowuje kinetic energy. Jeśli siła zostanie przyłożona do ciała mającego masęM, wtedy przeciwstawia się jej przeciwstawna siła ze względu na masę. Ta przeciwstawna siła jest proporcjonalna do przyspieszenia ciała. Załóżmy, że elastyczność i tarcie są znikome.

$$ F_m \ propto \: a $$
$$ \ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
$$ F = F_m = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
Gdzie,
F jest przyłożoną siłą
Fm jest siłą przeciwstawną spowodowaną masą
M jest masą
a to przyspieszenie
x jest przemieszczeniem
Wiosna
Wiosna to żywioł, który magazynuje potential energy. Jeśli na sprężynę zostanie przyłożona siłaK, to przeciwdziała mu siła przeciwstawna ze względu na elastyczność sprężyny. Ta przeciwstawna siła jest proporcjonalna do przemieszczenia sprężyny. Załóżmy, że masa i tarcie są nieistotne.

$$ F \ propto \: x $$
$$ \ Rightarrow F_k = Kx $$
$$ F = F_k = Kx $$
Gdzie,
F jest przyłożoną siłą
Fk jest siłą przeciwstawną wynikającą z elastyczności sprężyny
K jest stała sprężystością
x jest przemieszczeniem
Dashpot
Jeśli na deskę rozdzielczą zostanie przyłożona siła B, wtedy przeciwstawia się mu siła przeciwna ze względu na frictiondeski rozdzielczej. Ta przeciwstawna siła jest proporcjonalna do prędkości ciała. Załóżmy, że masa i elastyczność są pomijalne.

$$ F_b \ propto \: \ nu $$
$$ \ Rightarrow F_b = B \ nu = B \ frac {\ text {d} x} {\ text {d} t} $$
$$ F = F_b = B \ frac {\ text {d} x} {\ text {d} t} $$
Gdzie,
Fb jest siłą przeciwną wynikającą z tarcia deski rozdzielczej
B jest współczynnikiem tarcia
v to prędkość
x jest przemieszczeniem
Modelowanie obrotowych układów mechanicznych
Obrotowe systemy mechaniczne poruszają się wokół stałej osi. Systemy te składają się głównie z trzech podstawowych elementów. To sąmoment of inertia, torsional spring i dashpot.
Jeśli moment obrotowy jest przykładany do obrotowego układu mechanicznego, przeciwstawia się mu przeciwne momenty wynikające z momentu bezwładności, elastyczności i tarcia układu. Ponieważ przyłożony moment obrotowy i przeciwne momenty są w przeciwnych kierunkach, algebraiczna suma momentów działających na układ wynosi zero. Spójrzmy teraz indywidualnie na moment przeciwstawny przez te trzy elementy.
Moment bezwładności
W translacyjnym układzie mechanicznym masa magazynuje energię kinetyczną. Podobnie w obrotowym układzie mechanicznym, moment bezwładności magazynówkinetic energy.
Jeżeli moment obrotowy jest przykładany do ciała mającego moment bezwładności J, wtedy przeciwdziała mu przeciwny moment obrotowy z powodu momentu bezwładności. Ten przeciwny moment obrotowy jest proporcjonalny do kątowego przyspieszenia ciała. Załóżmy, że elastyczność i tarcie są znikome.

$$ T_j \ propto \: \ alpha $$
$$ \ Rightarrow T_j = J \ alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
$$ T = T_j = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
Gdzie,
T to zastosowany moment obrotowy
Tj to przeciwny moment obrotowy spowodowany momentem bezwładności
J jest moment bezwładności
α jest przyspieszeniem kątowym
θ jest przemieszczeniem kątowym
Sprężyna skrętna
W translacyjnym układzie mechanicznym sprężyna przechowuje energię potencjalną. Podobnie w obrotowym układzie mechanicznym, zapasy sprężyn skrętnychpotential energy.
Jeśli do sprężyny skrętnej zostanie przyłożony moment obrotowy K, następnie przeciwdziała mu przeciwny moment obrotowy ze względu na elastyczność sprężyny skrętnej. Ten przeciwny moment obrotowy jest proporcjonalny do kątowego przemieszczenia sprężyny skrętnej. Załóżmy, że moment bezwładności i tarcia są pomijalne.
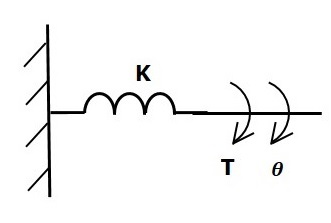
$$ T_k \ propto \: \ theta $$
$$ \ Rightarrow T_k = K \ theta $$
$$ T = T_k = K \ theta $$
Gdzie,
T to zastosowany moment obrotowy
Tk to przeciwny moment obrotowy wynikający z elastyczności sprężyny skrętnej
K jest stałą sprężyny skrętnej
θ jest przemieszczeniem kątowym
Dashpot
Jeśli na deskę rozdzielczą zostanie przyłożony moment obrotowy B, to jest przeciwny przez przeciwny moment obrotowy z powodu rotational frictiondeski rozdzielczej. Ten przeciwny moment obrotowy jest proporcjonalny do prędkości kątowej ciała. Załóżmy, że moment bezwładności i elastyczność są pomijalne.
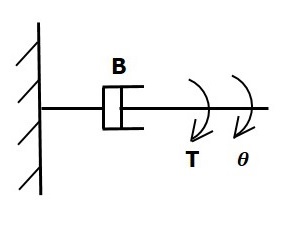
$$ T_b \ propto \: \ omega $$
$$ \ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
$$ T = T_b = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
Gdzie,
Tb to przeciwny moment obrotowy wynikający z tarcia obrotowego deski rozdzielczej
B jest współczynnikiem tarcia obrotowego
ω jest prędkością kątową
θ jest przemieszczeniem kątowym