ネットワーク理論-結合回路
電気回路は coupled circuit、その回路に存在するコイル(またはインダクタ)間に相互インダクタンスが存在する場合。コイルは、抵抗とインダクタの直列の組み合わせに他なりません。抵抗がない場合、コイルはインダクタになります。コイルとインダクタという用語は同じ意味で使用されることがあります。
この章では、最初にドットの規則について説明し、次に結合の分類について説明します。
ドットコンベンション
ドット規則は、ドット端子の電圧極性に関する詳細を提供する手法です。この情報は、KVL方程式を作成するときに役立ちます。
あるコイル(またはインダクタ)の点線の端子に電流が入ると、別のコイル(またはインダクタ)に電圧が誘導されます。 positive polarity 点線のターミナルで。
あるコイル(またはインダクター)の点線の端子から電流が出ると、別のコイル(またはインダクター)に電圧が誘導されます。 negative polarity 点線のターミナルで。
カップリングの分類
分類できます coupling 次の2つのカテゴリに分類されます。
- 電気的結合
- 磁気結合
それでは、それぞれのタイプのカップリングについて1つずつ説明しましょう。
電気的結合
電気的結合は、 physical connection2つのコイル(またはインダクタ)の間。このカップリングは、補助タイプまたは反対タイプのいずれかです。これは、電流が点線の端子から入るか、点線の端子から出るかに基づいています。
補助タイプのカップリング
次の電気回路を考えてみましょう。この回路には、2つのインダクタが接続されています。 series。
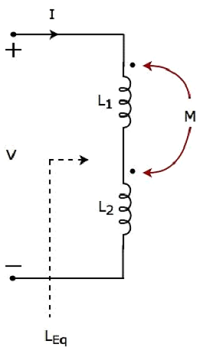
2つのインダクタが直列に接続されているため、 same current I自己インダクタンスLを有するインダクタの両方を通って流れ1及びL 2。
この場合、電流は各インダクタの点線端子から入ります。したがって、各インダクタの誘導電圧は次のようになります。positive polarity 別のコイルに電流が流れるため、点線の端子で。
適用する KVL 上記の電気回路またはネットワークのループの周り。
$$ V-L_1 \ frac {dI} {dt} -M \ frac {dI} {dt} -L_2 \ frac {dI} {dt} -M \ frac {dI} {dt} = 0 $$
$$ V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} + 2M \ frac {dI} {dt} $$
$$ V =(L_1 + L_2 + 2M)\ frac {dI} {dt} $$
上記の方程式は、$ \ mathbf {\ mathit {V = L_ {Eq} \ frac {dI} {dt}}} $の形式です。
したがって、 equivalent inductance 上図に示すインダクタの直列組み合わせの
$$ L_ {Eq} = L_1 + L_2 + 2M $$
この場合、等価インダクタンスは2M増加しています。したがって、上記の電気回路はelectrical のカップリング aiding タイプ。
対向型のカップリング
次の電気回路を考えてみましょう。この回路には、2つのインダクタが接続されています。 series。
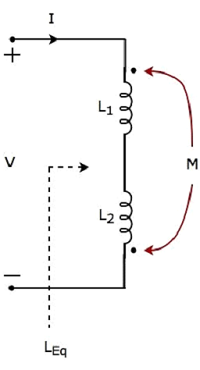
上記の回路では、電流 I のインダクタンスを持つインダクタの点線端子から入ります L1。したがって、インダクタンスが次のインダクタに電圧を誘導します。L2。そう、positive polarity 誘導電圧のは、このインダクタの点線端子に存在します。
上記の回路では、電流 I のインダクタンスを持つインダクタの点線端子から離れる L2。したがって、インダクタンスが次のインダクタに電圧を誘導します。L1。そう、negative polarity 誘導電圧のは、このインダクタの点線端子に存在します。
適用する KVL 上記の電気回路またはネットワークのループの周り。
$$ V-L_1 \ frac {dI} {dt} + M \ frac {dI} {dt} -L_2 \ frac {dI} {dt} + M \ frac {dI} {dt} = 0 $$
$$ \ Rightarrow V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} -2M \ frac {dI} {dt} $$
$$ \ Rightarrow V =(L_1 + L_2-2M)\ frac {dI} {dt} $$
上記の方程式は、$ \ mathbf {\ mathit {V = L_ {Eq} \ frac {dI} {dt}}} $の形式です。
したがって、 equivalent inductance 上図に示すインダクタの直列組み合わせの
$$ L_ {Eq} = L_1 + L_2-2M $$
この場合、等価インダクタンスは2M減少しています。したがって、上記の電気回路はelectrical のカップリング opposing タイプ。
磁気結合
磁気結合が発生すると、 no physical connection2つのコイル(またはインダクタ)の間。このカップリングは、補助タイプまたは反対タイプのいずれかです。これは、電流が点線の端子から入るか、点線の端子から出るかに基づいています。
補助タイプのカップリング
次の電気的同等物を検討してください circuit of transformer。それは2つのコイルを持っており、これらは一次コイルと二次コイルと呼ばれます。
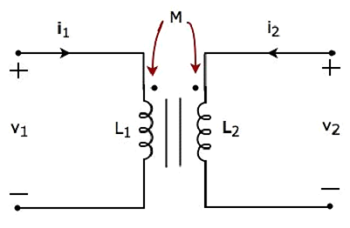
一次および二次コイルに流れる電流はIである1とI 2をそれぞれ。この場合、これらの電流enterそれぞれのコイルの点線の端子で。したがって、各コイルの誘導電圧は、別のコイルに電流が流れるため、点線の端子で正極性になります。
適用する KVL 一次コイルの周り。
$$ v_1-L_1 \ frac {d i_1} {dt} -M \ frac {d i_2} {dt} = 0 $$
$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} $Equation 1
適用する KVL 二次コイルの周り。
$$ v_2-L_2 \ frac {d i_2} {dt} -M \ frac {d i_1} {dt} = 0 $$
$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} $Equation 2
式1と式2では、自己誘導電圧と相互誘導電圧は同じ極性を持っています。したがって、上記のトランス回路はmagnetic coupling、の aiding タイプ。
反対型のカップリング
次の電気的同等物を検討してください circuit of transformer。

一次および二次コイルに流れる電流はIである1とI 2をそれぞれ。この場合、電流は、I 1は、一次コイルのドット端末に入ります。したがって、2次コイルに電圧を誘導します。そう、positive polarity 誘導電圧の1つは、この2次コイルの点線端子に存在します。
上記回路において、電流、I 2二次コイルのドット端末からの葉。したがって、一次コイルに電圧を誘導します。そう、negative polarity 誘導電圧のは、この一次コイルの点線端子に存在します。
適用する KVL 一次コイルの周り。
$$ v_1-L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} = 0 $$
$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} -M \ frac {d i_2} {dt} $Equation 3
適用する KVL 二次コイルの周り。
$$ v_2-L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} = 0 $$
$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} -M \ frac {d i_1} {dt} $Equation 4
式3と式4では、自己誘導電圧と相互誘導電圧の極性が逆になっています。したがって、上記のトランス回路はmagnetic coupling、の opposing タイプ。