最大電力伝達定理
負荷が受け取る電力量は、電気および電子アプリケーションの重要なパラメータです。直流回路では、我々は、Rの抵抗値を有する抵抗で負荷を表すことができるLのオーム。同様に、交流回路において、我々は、Zのインピーダンスを有する複合負荷でそれを表すことができるLのオーム。
Maximum power transfer theorem DC電圧源は、負荷抵抗がソース抵抗と等しい場合にのみ、可変負荷抵抗に最大電力を供給すると述べています。
同様に、 Maximum power transfer theorem AC電圧源は、負荷インピーダンスがソースインピーダンスの複素共役に等しい場合にのみ、可変複素負荷に最大電力を供給すると述べています。
この章では、DC回路の最大電力伝達定理について説明します。
最大電力伝達定理の証明
Rの抵抗値を有する可変負荷抵抗の左側に任意の二つの末端線ネットワークまたは回路交換Lのテブナンの等価回路とのオーム。テブナンの等価回路は実際の電圧源に似ていることがわかっています。
この概念を次の図に示します。
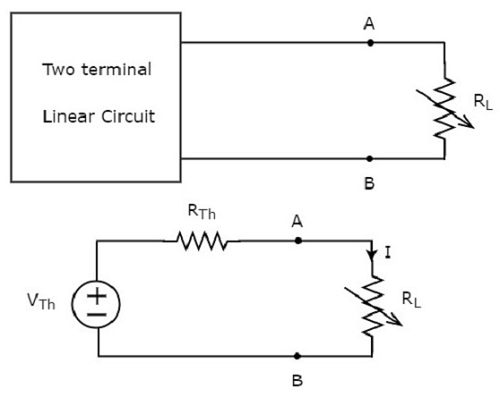
負荷抵抗の両端で消費される電力量は次のとおりです。
$$ P_L = I ^ 2 R_L $$
上記の式に$ I = \ frac {V_ {Th}} {R_ {Th} + R_L} $を代入します。
$$ P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L $$
$ \ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L)^ 2} \ rbrace $ Equation 1
最大電力伝達の条件
最大または最小の場合、一次導関数はゼロになります。したがって、式1をR Lに関して微分し、ゼロに等しくします。
$$ \ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L)^ 2 \ times 1-R_L \ times 2(R_ {Th} + R_L) } {(R_ {Th} + R_L)^ 4} \ rbrace = 0 $$
$$ \ Rightarrow(R_ {Th} + R_L)^ 2 -2R_L(R_ {Th} + R_L)= 0 $$
$$ \ Rightarrow(R_ {Th} + R_L)(R_ {Th} + R_L-2R_L)= 0 $$
$$ \ Rightarrow(R_ {Th} -R_L)= 0 $$
$$ \ Rightarrow R_ {Th} = R_L \:or \:R_L = R_ {Th} $$
したがって、 condition for maximum power負荷全体の消費電力は$ R_L = R_ {Th} $です。つまり、負荷抵抗の値がソース抵抗の値、つまりテブナンの抵抗と等しい場合、負荷全体で消費される電力は最大値になります。
最大電力伝達の値
式1に$ R_L = R_ {Th} \:\&\:P_L = P_ {L、Max} $を代入します。
$$ P_ {L、Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th})^ 2} \ rbrace $$
$$ P_ {L、Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace $$
$$ \ Rightarrow P_ {L、Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
$$ \ Rightarrow P_ {L、Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}、\:\:R_ {L} = R_ {Th} $$以降
したがって、 maximum amount of power 負荷に転送されます
$$ P_ {L、最大} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} $$
最大電力伝達の効率
次の式を使用して、最大電力伝達の効率$ \ eta_ {Max} $を計算できます。
$ \ eta_ {Max} = \ frac {P_ {L、Max}} {P_S} $ Equation 2
どこ、
$ P_ {L、Max} $は、負荷に転送される電力の最大量です。
$ P_S $は、ソースによって生成された電力量です。
ザ・ amount of power generated ソースによってです
$$ P_S = I ^ 2 R_ {Th} + I ^ 2 R_L $$
$$ \ Rightarrow P_S = 2 I ^ 2 R_ {Th}、\:since \:R_ {L} = R_ {Th} $$
上記の式に$ I = \ frac {V_ {Th}} {2 R_ {Th}} $を代入します。
$$ P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th} $$
$$ \ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th} $$
$$ \ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th}} $$
式2の$ P_ {L、Max} $と$ P_S $の値を代入します。
$$ \ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} { 2R_ {Th}} \ rgroup} $$
$$ \ Rightarrow \ eta_ {Max} = \ frac {1} {2} $$
最大電力伝達の効率を次のように表すことができます。 percentage 次のように-
$$ \%\ eta_ {Max} = \ eta_ {Max} \ times 100 \%$$
$$ \ Rightarrow \%\ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ times 100 \%$$
$$ \ Rightarrow \%\ eta_ {Max} = 50 \%$$
したがって、最大電力伝達の効率は次のようになります。 50 %。
例
を見つける maximum powerそれは、負荷抵抗Rに送達することができるL以下の図に示す回路。
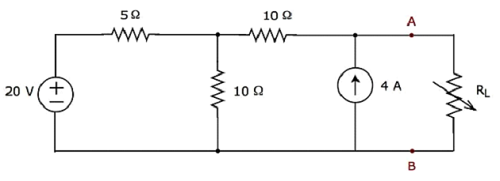
Step 1−テブナンの定理の章では、端子AとBの左側にあるテブナンの等価回路を計算しました。これでこの回路を使用できます。次の図に示します。
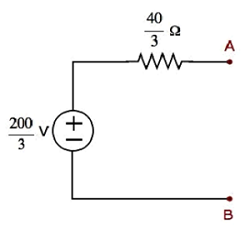
ここで、テブナンの電圧$ V_ {Th} = \ frac {200} {3} V $とテブナンの抵抗$ R_ {Th} = \ frac {40} {3} \ Omega $
Step 2−所定の回路の端子AとBの左側にある回路の部分を、上記のテブナンの等価回路に置き換えます。結果の回路図を次の図に示します。

Step 3-我々は、負荷抵抗Rに配信される最大電力見つけることができるL以下の式を使用しています。
$$ P_ {L、最大} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
上記の式に$ V_ {Th} = \ frac {200} {3} V $と$ R_ {Th} = \ frac {40} {3} \ Omega $を代入します。
$$ P_ {L、最大} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup} $$
$$ P_ {L、最大} = \ frac {250} {3} W $$
したがって、 maximum power 与えられた回路の負荷抵抗RLに供給されるのは$ \ mathbf {\ frac {250} {3}} $です。 W