ネットワーク理論-テブナンの定理
Thevenin’s theoremは、任意の2端子線形ネットワークまたは回路を、抵抗と直列の電圧源で構成される同等のネットワークまたは回路で表すことができると述べています。テブナンの等価回路として知られています。線形回路には、独立したソース、依存したソース、および抵抗が含まれる場合があります。
回路に複数の独立したソース、依存したソース、および抵抗が含まれている場合、要素の左側にあるネットワーク全体を次のように置き換えることで、要素の応答を簡単に見つけることができます。 Thevenin’s equivalent circuit。
ザ・ response in an element その要素の両端の電圧、その要素を流れる電流、またはその要素の両端で消費される電力のいずれかです。
この概念を次の図に示します。
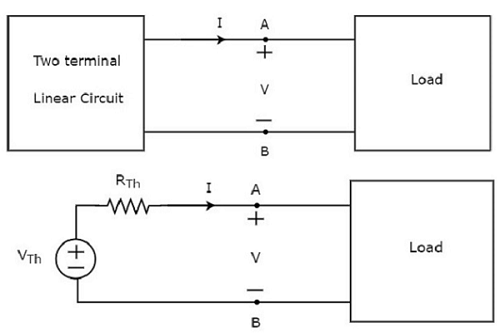
Thevenin’s equivalent circuit実用的な電圧源に似ています。したがって、抵抗と直列に電圧源があります。
テブナンの等価回路に存在する電圧源は、テブナンの等価電圧または単に呼ばれます。 Thevenin’s voltage, VTh。
テブナンの等価回路に存在する抵抗は、テブナンの等価抵抗または単に呼ばれます。 Thevenin’s resistor, RTh。
テブナンの等価回路を見つける方法
テブナンの等価回路を見つけるには3つの方法があります。に基づくtype of sourcesネットワークに存在する場合、これら3つの方法のいずれかを選択できます。それでは、2つの方法を1つずつ説明しましょう。次の章では、3番目の方法について説明します。
方法1
テブナンの等価回路を見つけるには、次の手順に従ってください。 sources of independent type 存在しています。
Step 1 −テブナンの等価回路を見つけるための端子を開いて回路図を検討します。
Step 2 −テブナンの電圧を見つける VTh 上記の回路のオープン端子間。
Step 3 −テブナンの抵抗を見つける RTh その中に存在する独立したソースを排除することにより、上記の回路のオープン端子間で。
Step 4 −を描く Thevenin’s equivalent circuitテブナンの電圧Vの接続によってのThをテブナンの抵抗Rと直列のTh。
これで、テブナンの等価回路の右側にある要素で応答を見つけることができます。
例
最初にaを見つけて、20Ωの抵抗を流れる電流を見つけます。 Thevenin’s equivalent circuit 端子AとBの左側。
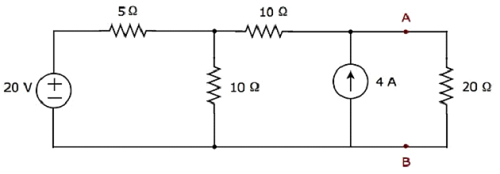
Step 1 −端子AとBの左側にあるテブナンの等価回路を見つけるには、次の方法でネットワークから20Ωの抵抗を削除する必要があります。 opening the terminals A & B。変更した回路図を次の図に示します。
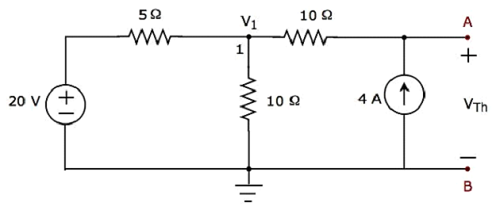
Step 2 −の計算 Thevenin’s voltage VTh。
上記の回路では、グラウンドを除いて主要ノードは1つだけです。だから、私たちは使用することができますnodal analysis方法。ノード電圧V 1とテブナンの電圧V Thが上記の図に標識されます。ここで、V 1はグランドに対するノード1からの電圧であり、VThは4A電流源の両端の電圧です。
ザ・ nodal equation ノード1には
$$ \ frac {V_1-20} {5} + \ frac {V_1} {10} -4 = 0 $$
$$ \ Rightarrow \ frac {2V_1-40 + V_1-40} {10} = 0 $$
$$ \ Rightarrow 3V_1-80 = 0 $$
$$ \ Rightarrow V_1 = \ frac {80} {3} V $$
直列分岐10Ω抵抗の両端の電圧は
$$ V_ {10 \ Omega} =(-4)(10)= -40V $$
上記の回路には2つのメッシュがあります。ザ・KVL equation 2番目のメッシュの周りは
$$ V_1-V_ {10 \ Omega} -V_ {Th} = 0 $$
上記の式に$ V_1 $と$ V_ {10 \ Omega} $の値を代入します。
$$ \ frac {80} {3}-(-40)-V_ {Th} = 0 $$
$$ V_ {Th} = \ frac {80 + 120} {3} = \ frac {200} {3} V $$
したがって、テブナンの電圧は$ V_ {Th} = \ frac {200} {3} V $です。
Step 3 −の計算 Thevenin’s resistance RTh。
短絡電圧源と開回路テブナンの抵抗値Rを計算するために、上記の回路の電流源のThを端子A&B.ザを横切ってmodified circuit diagram 次の図に示します。
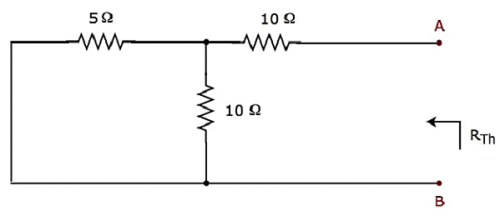
端子AとB間のテブナンの抵抗は
$$ R_ {Th} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
したがって、テブナンの抵抗は$ \ mathbf {R_ {Th} = \ frac {40} {3} \ Omega} $です。
Step 4−テブナンの等価回路は、指定された回路の端子AとBの左側に配置されます。この回路図を次の図に示します。

20Ωの抵抗を流れる電流は、の値を代入することによって求めることができるV Thを、RのTh及びRを次式で。
$$ l = \ frac {V_ {Th}} {R_ {Th} + R} $$
$$ l = \ frac {\ frac {200} {3}} {\ frac {40} {3} + 20} = \ frac {200} {100} = 2A $$
したがって、20Ωの抵抗を流れる電流は 2 A。
方法2
テブナンの等価回路を見つけるには、次の手順に従ってください。 sources of both independent type and dependent type 存在しています。
Step 1 −テブナンの等価回路が見つかる端子を開いて、回路図を検討します。
Step 2 −テブナンの電圧を見つける VTh 上記の回路のオープン端子間。
Step 3 −短絡電流を見つける ISC 上記の回路の2つの開いた端子を短絡することによって。
Step 4 −テブナンの抵抗を見つける RTh 次の式を使用します。
$$ R_ {Th} = \ frac {V_ {Th}} {I_ {SC}} $$
Step 5 −を描く Thevenin’s equivalent circuitテブナンの電圧Vの接続によってのThをテブナンの抵抗Rと直列のTh。
これで、テブナンの等価回路の右側にある要素で応答を見つけることができます。