ネットワーク理論-スターからデルタへの変換
前の章では、デルタネットワークの同等のスターネットワークへの変換について説明しました。それでは、スターネットワークから同等のデルタネットワークへの変換について説明しましょう。この変換は、Star to Delta Conversion。
前の章では、 resistances of star network デルタネットワークから
$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ Equation 3
スターネットワーク抵抗の観点からのデルタネットワーク抵抗
スターネットワークの抵抗の観点からデルタネットワークの抵抗を取得するために、上記の方程式を操作してみましょう。
Multiply 2つの方程式の各セットそして add。
$$ R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 ^ 2 R_3 + R_2 R_3 ^ 2 R_1 + R_3 R_1 ^ 2 R_2} {(R_1 + R_2 + R_3)^ 2} $$
$$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3(R_1 + R_2 + R_3)} {(R_1 + R_2 + R_3)^ 2} $$
$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3} {R_1 + R_2 + R_3} $ Equation 4
式4を式2で割ると、次のようになります。
$$ \ frac {R_A R_B + R_B R_C + R_C R_A} {R_B} = R_1 $$
$$ \ Rightarrow R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
式4を式3で割ると、次のようになります。
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
式4を式1で割ると、次のようになります。
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
上記の関係を使用することにより、スターネットワークの抵抗からデルタネットワークの抵抗を見つけることができます。このようにして、変換することができますstar network into delta network。
例
計算してみましょう resistances of delta network、次の図に示すように、スターネットワークと同等です。
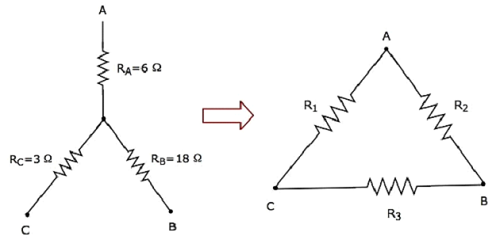
与えられた resistances of star networkR A = 6Ω、R B = 18Ω及びR C = 3Ω。
私たちは次の関係を知っています resistances of delta network スターネットワークの抵抗の観点から。
$$ R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
値を代入R A、R BおよびR Cが上記の式に。
$$ R_1 = 3 + 6 + \ frac {3 \ times 6} {18} = 9 + 1 = 10 \ Omega $$
$$ R_2 = 6 + 18 + \ frac {6 \ times 18} {3} = 24 + 36 = 60 \ Omega $$
$$ R_3 = 18 + 3 + \ frac {18 \ times 3} {6} = 21 + 9 = 30 \ Omega $$
したがって、デルタネットワークの抵抗は次のようになります。 R1 = 10 Ω, R2 = 60 Ω そして R3 = 30 Ω、これは特定のスターネットワークの抵抗に相当します。