ネットワークトポロジマトリックス
前の章では、電気回路を同等のグラフに変換する方法について説明しました。次に、同等のグラフを使用して、電気回路またはネットワークの問題を解決するのに役立つネットワークトポロジ行列について説明します。
ネットワークグラフに関連付けられた行列
以下は、グラフ理論で使用される3つの行列です。
- 接続行列
- 基本的なループマトリックス
- ファンダメンタルカットセットマトリックス
接続行列
接続行列は、特定の電気回路またはネットワークのグラフを表します。したがって、同じ電気回路またはネットワークのグラフをから描くことができます。incidence matrix。
グラフはノードのセットで構成されており、それらはいくつかのブランチで接続されていることがわかっています。したがって、ブランチをノードに接続することを発生率と呼びます。接続行列は文字Aで表されます。これは、ノードから分岐への接続行列またはnode incidence matrix。
'n'ノードがあり、 'b'ブランチがaに存在する場合 directed graphの場合、接続行列には「n」行と「b」列があります。ここで、行と列は有向グラフのノードとブランチに対応しています。従ってorder 接続行列の n × b。
ザ・ elements of incidence matrix + 1、-1、0の3つの値のいずれかになります。
分岐電流が選択したノードから出ている場合、要素の値は+1になります。
分岐電流が選択したノードに向かって入っている場合、要素の値は-1になります。
分岐電流が選択されたノードに流入せず、選択されたノードから流出しない場合、要素の値は0になります。
接続行列を見つける手順
有向グラフの接続行列を見つけるには、次の手順に従います。
指定された有向グラフの時点でノードを選択し、そのノードに対応する接続行列の要素の値を行に入力します。
指定された有向グラフのすべてのノードに対して上記の手順を繰り返します。
例
次のことを考慮してください directed graph。

ザ・ incidence matrix 上記の有向グラフに対応します
$$ A = \ begin {bmatrix} -1&1&0&-1&0&0 \\ 0&-1&1&0&1&0 \\ 1&0&-1&0&0&1 \\ 0&0&0&1&-1&-1 \ end {bmatrix} $$
上記の行列の行と列は、指定された有向グラフのノードとブランチを表します。この接続行列の次数は4×6です。
上記の接続行列を観察することにより、次のように結論付けることができます。 summation接続行列の列要素の数はゼロに等しい。つまり、分岐電流は1つのノードから出て、別の単一ノードにのみ入ります。
Note−与えられたグラフが無向タイプの場合、その各ブランチの矢印を表すことにより、それを有向グラフに変換します。各分岐に流れる電流の任意の方向を考慮することができます。
基本的なループマトリックス
基本的なループまたは f-loopはループであり、1つのリンクと1つ以上の小枝のみが含まれています。したがって、fループの数はリンクの数と等しくなります。基本的なループ行列は文字Bで表されます。これは次のようにも呼ばれます。fundamental circuit matrixおよびタイセット行列。この行列は、分岐電流とリンク電流の関係を示します。
'n'ノードがあり、 'b'ブランチがaに存在する場合 directed graphの場合、指定されたグラフの選択されたツリーに対応する、コツリーに存在するリンクの数はb-n +1になります。
したがって、基本ループ行列には「b-n +1」行と「b」列があります。ここで、行と列は、指定されたグラフのコツリーとブランチのリンクに対応しています。したがって、基本ループ行列の次数は次のようになります。(b - n + 1) × b。
ザ・ elements of fundamental loop matrix + 1、-1、0の3つの値のいずれかになります。
選択したfループのリンクの要素の値は+1になります。
選択したfループの一部ではない残りのリンクと小枝の要素の値は0になります。
選択したfループの小枝電流の方向がfループリンク電流の方向と同じである場合、要素の値は+1になります。
選択したfループの小枝電流の方向がfループリンク電流の方向と反対の場合、要素の値は-1になります。
基本的なループ行列を見つける手順
与えられた有向グラフの基本的なループ行列を見つけるために、これらのステップに従ってください。
与えられた有向グラフのツリーを選択します。
一度に1つのリンクを含めることにより、1つのfループを取得します。このfループに対応する要素の値を基本ループ行列の行に入力します。
すべてのリンクに対して上記の手順を繰り返します。
例
次のツリーを見てください directed graph、これは接続行列と見なされます。

上記のツリーには、3つのブランチd、e、fが含まれています。したがって、ブランチa、b、cは、上記のツリーに対応するCo-Treeのリンクになります。上記のツリーへのリンクを一度に1つ含めると、1つになります。f-loop。だから、3つありますf-loops、3つのリンクがあるため。これらの3つのfループを次の図に示します。
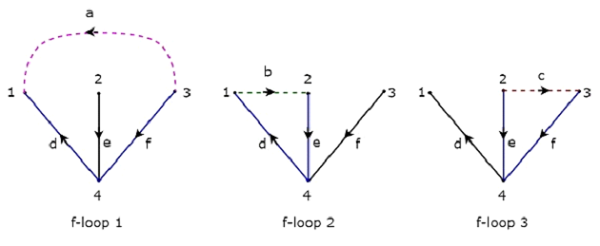
上の図では、色付きの線で表されているブランチがfループを形成しています。各fループからタイセット行列の行ごとの要素値を取得します。だから、Tieset matrix 上記の考慮されたツリーの
$$ B = \ begin {bmatrix} 1&0&0&-1&0&-1 \\ 0&1&0&1&1&0 \\ 0&0&1&0&-1&1 \ end {bmatrix} $$
上記の行列の行と列は、指定された有向グラフのリンクとブランチを表しています。この接続行列の次数は3×6です。
ザ・ number of Fundamental loop matrices有向グラフの数は、その有向グラフのツリーの数に等しくなります。なぜなら、すべてのツリーには1つの基本ループ行列があるからです。
基本的なカットセットマトリックス
ファンダメンタルカットセットまたは f-cut setは、元のグラフが2つの分離されたサブグラフになるようにグラフから削除されるブランチの最小数です。Fカットセットにはone twigおよび1つ以上のリンク。したがって、fカットセットの数は小枝の数と同じになります。
Fundamental cut set matrix は文字Cで表されます。この行列は、分岐電圧と小枝電圧の関係を示します。
'n'ノードがあり、 'b'ブランチがaに存在する場合 directed graphの場合、指定されたグラフの選択されたツリーに存在する小枝の数はn-1になります。したがって、基本的なカットセット行列には「n-1」行と「b」列があります。ここで、行と列は、選択したツリーの小枝と特定のグラフの枝に対応しています。従ってorder 基本カットセットマトリックスの (n-1) × b。
ザ・ elements of fundamental cut set matrix + 1、-1、0の3つの値のいずれかになります。
要素の値は、選択したfカットセットの小枝に対して+1になります。
選択したfカットセットの一部ではない残りの小枝とリンクの要素の値は0になります。
選択したfカットセットのリンク電流の方向がfカットセットの小枝電流の方向と同じである場合、要素の値は+1になります。
選択したfカットセットのリンク電流の方向がfカットセットの小枝電流の方向と反対の場合、要素の値は-1になります。
基本的なカットセットマトリックスを見つける手順
与えられた有向グラフの基本的なカットセット行列を見つけるために、これらのステップに従ってください。
与えられた有向グラフのツリーを選択し、点線でリンクを表します。
一度に1本の小枝と必要なリンクを取り除くことで、1つのfカットセットを手に入れることができます。このfカットセットに対応する要素の値を基本カットセット行列の行に入力します。
すべての小枝に対して上記の手順を繰り返します。
例
同じことを考えてください directed graph 、接続行列のセクションで説明しました。この有向グラフのブランチd、e、fを小枝として選択します。したがって、この有向グラフの残りのブランチa、b、cがリンクになります。
ザ・ twigs d、e、fは実線で表され、 links 次の図では、a、b、cが点線で表されています。
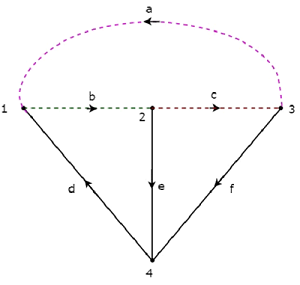
一度に1本の小枝と必要なリンクを取り除くことで、1つのfカットセットを手に入れることができます。つまり、小枝が3つあるので、fカットセットは3つになります。これらの3つf-cut sets 次の図に示します。

C 1、C 2、C 3の小枝とリンクのセットを削除することにより、3つのfカットセットを作成します。各fカットセットから基本カットセット行列の行ごとの要素値を取得します。だから、fundamental cut set matrix 上記の考慮されたツリーの
$$ C = \ begin {bmatrix} 1&-1&0&1&0&0 \\ 0&-1&1&0&1&0 \\ 1&0&-1&0&0&1 \ end {bmatrix} $$
上記の行列の行と列は、指定された有向グラフの小枝と枝を表しています。この基本的なカットセット行列の次数は3×6です。
ザ・ number of Fundamental cut set matrices有向グラフの数は、その有向グラフのツリーの数に等しくなります。なぜなら、すべてのツリーには1つの基本カットセットマトリックスがあるからです。