ネットワーク理論-キルヒホッフの法則
ネットワーク要素は、次のいずれかになります。 active または passiveタイプ。電気回路またはネットワークには、これら2種類のネットワーク要素のいずれかまたは両方の組み合わせが含まれています。
それでは、一般に次の2つの法則について説明します。 Kirchhoff’s laws。
- キルヒホッフの現行法
- キルヒホッフの電圧法則
キルヒホッフの現行法
キルヒホッフの現在の法則(KCL)は、ノードを出る(または入る)電流の代数和はゼロに等しいと述べています。
A Node2つ以上の回路要素が接続されているポイントです。1つのノードに2つの回路要素のみが接続されている場合、それは単純ノードと呼ばれます。3つ以上の回路要素がノードに接続されている場合、それはPrincipal Node。
Mathematically、KCLは次のように表すことができます
$$ \ displaystyle \ sum \ Limits_ {m = 1} ^ M I_m = 0 $$
どこ、
Imノードを出るm番目の分岐電流です。
M ノードに接続されているブランチの数です。
上記のステートメント KCL「ノードに入る電流の代数和は、ノードから出る電流の代数和に等しい」と表現することもできます。次の例でこのステートメントを確認しましょう。
例
書く KCL equation ノードで P 次の図の。
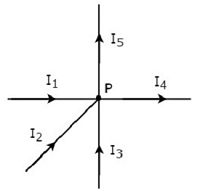
上の図では、分岐電流I 1、I 2とI 3がありますentering ノードPで。したがって、これら3つの電流の負の符号を考慮してください。
上の図で、枝電流I 4とI 5ですleaving ノードPから。したがって、これら2つの電流の正の符号を考慮してください。
ザ・ KCL equation ノードPで
$$-I_1 --I_2 --I_3 + I_4 + I_5 = 0 $$
$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$
上記の式で、左辺は流入電流の合計を表し、右辺は流出電流の合計を表します。
このチュートリアルでは、電流がノードを離れるときは正の符号を、ノードに入るときは負の符号を検討します。同様に、電流がノードを離れるときは負の符号を、ノードに入るときは正の符号を考慮することができます。どちらの場合も、result will be same。
Note − KCLは、ノードに接続されているネットワーク要素の性質に依存しません。
キルヒホッフの電圧法則
キルヒホッフの電圧法則(KVL)は、ループまたはメッシュの周りの電圧の代数和がゼロに等しいと述べています。
A Loopは、開始元と同じノードで終了するパスです。対照的に、Mesh は、内部に他のループを含まないループです。
数学的には、KVLは次のように表すことができます。
$$ \ displaystyle \ sum \ Limits_ {n = 1} ^ N V_n = 0 $$
どこ、
Vnループ(メッシュ)内のn番目の要素の電圧です。
N ループ(メッシュ)内のネットワーク要素の数です。
上記のステートメント KVL「電圧源の代数和は、ループ内に存在する電圧降下の代数和に等しい」と表現することもできます。次の例を使用して、このステートメントを確認しましょう。
例
書く KVL equation 次の回路のループの周り。
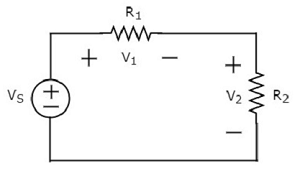
上記の回路図は、電圧源Vから成るS二つの抵抗をRと直列に1及びR 2。抵抗Rの両端の電圧は降下1及びR 2がVである1及びV 2はそれぞれ。
適用する KVL ループの周り。
$$ V_S-V_1-V_2 = 0 $$
$$ \ Rightarrow V_S = V_1 + V_2 $$
上記の式で、左辺の項は単一の電圧源VSを表します。一方、右側はsum of voltage drops。この例では、1つの電圧源のみを考慮しました。そのため、左側には1つの用語しか含まれていません。複数の電圧源を検討する場合、左側には電圧源の合計が含まれます。
このチュートリアルでは、各要素の電圧の符号を、ループ内を移動するときに存在する2番目の端子の極性と見なします。同様に、各電圧の符号は、ループを移動しているときに存在する最初の端子の極性と見なすことができます。どちらの場合も、result will be same。
Note − KVLは、ループ内に存在するネットワーク要素の性質に依存しません。