ネットワーク理論-デルタからスターへの変換
前の章では、等価抵抗に関連する問題の例について説明しました。そこで、計算しましたequivalent resistance与えられた電気ネットワークの端子AとBの間で簡単に。なぜなら、すべてのステップで、直列形式または並列形式のいずれかで接続された抵抗の組み合わせを取得したからです。
ただし、状況によっては、以前のアプローチに従ってネットワークを単純化することが難しい場合があります。たとえば、デルタ(δ)形式またはスター形式のいずれかで接続された抵抗。そのような状況では、私たちはしなければなりませんconvert直列の組み合わせまたは並列の組み合わせを使用してさらに単純化するために、ある形式から別の形式のネットワーク。この章では、Delta to Star Conversion。
デルタネットワーク
次のことを考慮してください delta network 次の図に示すように。
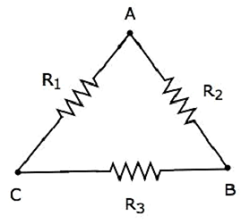
次の式は、 equivalent resistance デルタネットワークの2つの端末間で、3番目の端末が開いたままの場合。
$$ R_ {AB} = \ frac {(R_1 + R_3)R_2} {R_1 + R_2 + R_3} $$
$$ R_ {BC} = \ frac {(R_1 + R_2)R_3} {R_1 + R_2 + R_3} $$
$$ R_ {CA} = \ frac {(R_2 + R_3)R_1} {R_1 + R_2 + R_3} $$
スターネットワーク
次の図は、 equivalent star network 上記のデルタネットワークに対応します。
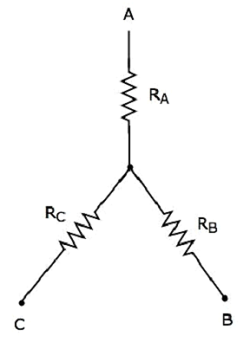
次の式は、 equivalent resistance スターネットワークの2つの端末間で、3番目の端末が開いたままの場合。
$$ R_ {AB} = R_A + R_B $$
$$ R_ {BC} = R_B + R_C $$
$$ R_ {CA} = R_C + R_A $$
デルタネットワーク抵抗の観点からのスターネットワーク抵抗
上記の方程式の左辺の項が同じである右辺の項を等しくすることにより、次の方程式が得られます。
$ R_A + R_B = \ frac {(R_1 + R_3)R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B + R_C = \ frac {(R_1 + R_2)R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C + R_A = \ frac {(R_2 + R_3)R_1} {R_1 + R_2 + R_3} $ Equation 3
上記の3つの方程式を追加すると、次のようになります。
$$ 2(R_A + R_B + R_C)= \ frac {2(R_1 R_2 + R_2 R_3 + R_3 R_1)} {R_1 + R_2 + R_3} $$
$ \ Rightarrow R_A + R_B + R_C = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} $ Equation 4
式4から式2を引きます。
$ R_A + R_B + R_C-(R_B + R_C)= \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3}-\ frac {(R_1 + R_2)R_3} {R_1 + R_2 + R_3} $
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
式4から式3を引くと、次のようになります。
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
式4から式1を引くと、次のようになります。
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
上記の関係を使用することにより、デルタネットワークの抵抗からスターネットワークの抵抗を見つけることができます。このようにして、delta network に star network。
例
計算してみましょう resistances of star network、次の図に示すように、デルタネットワークと同等です。
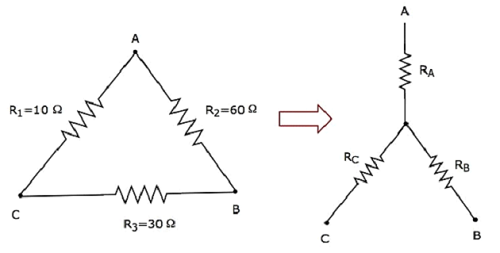
与えられた resistances of delta networkR 1 = 10Ω、R 2 = 60ΩかつR 3 = 30Ω。
デルタネットワークの抵抗の観点から、スターネットワークの抵抗の次の関係を知っています。
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
値を代入R 1、R 2及びR 3は上記式に。
$$ R_A = \ frac {10 \ times 60} {10 + 60 + 30} = \ frac {600} {100} = 6 \ Omega $$
$$ R_B = \ frac {60 \ times 30} {10 + 60 + 30} = \ frac {1800} {100} = 18 \ Omega $$
$$ R_C = \ frac {30 \ times 10} {10 + 60 + 30} = \ frac {300} {100} = 3 \ Omega $$
だから、私たちはスターネットワークの抵抗を得ました RA = 6 Ω, RB = 18 Ω そして RC = 3 Ω、これは、特定のデルタネットワークの抵抗に相当します。