ネットワーク理論-重ね合わせの原理
Superposition theorem電気回路の応答と励起の間の線形性の概念に基づいています。複数の独立したソースが同時に動作している場合の線形回路の特定の分岐での応答は、各独立したソースが同時に動作しているための応答の合計に等しいと述べています。
この方法では、のみを考慮します one independent source一度に。したがって、回路から残りの独立したソースを排除する必要があります。2つの端子を短絡することで電圧源を排除でき、同様に2つの端子を開くことで電流源を排除できます。
したがって、特定のブランチで応答を見つける必要があります ‘n’ times'n'の独立したソースがある場合。特定のブランチでの応答は、そのブランチを流れる電流またはそのブランチの両端の電圧のいずれかである可能性があります。
重ね合わせの原理の手順
重ね合わせの原理を使用して特定のブランチの応答を見つけるには、次の手順に従います。
Step 1 − 1つの独立したソースを検討し、ネットワークに存在する残りの独立したソースを排除することにより、特定のブランチでの応答を見つけます。
Step 2 −ネットワークに存在するすべての独立したソースに対して手順1を繰り返します。
Step 3 −すべての独立したソースがネットワークに存在する場合に特定のブランチで全体的な応答を取得するために、すべての応答を追加します。
例
次の回路の20Ω抵抗を流れる電流を superposition theorem。
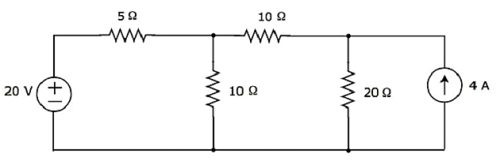
Step 1 −20Ω抵抗を流れる電流を考慮してみよう 20 V voltage source。この場合、4Aの電流源を開回路にすることで電流源をなくすことができます。変更した回路図を次の図に示します。

上記の回路では、グラウンドを除いて主要ノードは1つだけです。だから、私たちは使用することができますnodal analysis方法。ノード電圧V 1は、次の図に標識されます。ここで、V 1は、ノード1からのグランドに対する電圧です。
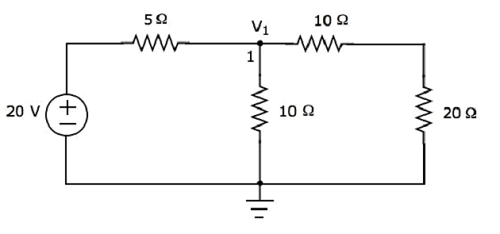
ザ・ nodal equation ノード1には
$$ \ frac {V_1-20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$
$$ \ Rightarrow \ frac {6V_1-120 + 3V_1 + V_1} {30} = 0 $$
$$ \ Rightarrow 10V_1 = 120 $$
$$ \ Rightarrow V_1 = 12V $$
ザ・ current flowing through 20 Ω resistor 次の簡略化を行うことで見つけることができます。
$$ I_1 = \ frac {V_1} {10 + 20} $$
Vの値が代入1を上式に。
$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0.4 A $$
したがって、20Ωの抵抗を流れる電流は 0.4 A、20Vの電圧源のみを考慮した場合。
Step 2 −20Ω抵抗を流れる電流を考慮してみよう 4 A current source。この場合、20Vの電圧源を短絡させることで除去できます。変更した回路図を次の図に示します。
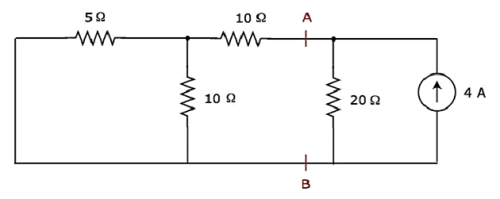
上記の回路では、端子AとBの左側に3つの抵抗があります。これらの抵抗を1つの抵抗に置き換えることができます。 equivalent resistor。ここでは、5Ωと10Ωの抵抗が並列に接続されており、組み合わせ全体が10Ωの抵抗と直列になっています。
ザ・ equivalent resistance 端子AとBの左側は
$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
簡略化した回路図を次の図に示します。
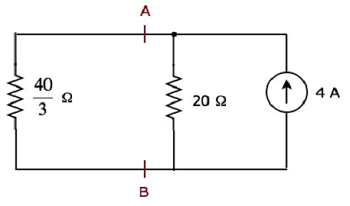
を使用して、20Ωの抵抗を流れる電流を見つけることができます current division principle。
$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
上記の式に$ I_S = 4A、\:R_1 = \ frac {40} {3} \ Omega $と$ R_2 = 20 \ Omega $を代入します。
$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1.6 A $$
したがって、20Ωの抵抗を流れる電流は 1.6 A、4Aの電流源のみを考慮した場合。
Step 3 −与えられた回路の20Ω抵抗を流れる電流を得るには、 addition of two currents ステップ1とステップ2で得たものです。数学的には、次のように書くことができます。
$$ I = I_1 + I_2 $$
代替の値I 1及びI 2上記の式です。
$$ I = 0.4 + 1.6 = 2 A $$
したがって、特定の回路の20Ω抵抗を流れる電流は次のようになります。 2 A。
Note −の量を求めるために、重ね合わせの原理を直接適用することはできません。 power線形回路に存在する任意の抵抗器に供給され、それぞれの独立したソースによってその抵抗器に供給される電力を追加するだけです。むしろ、重ね合わせの原理を使用して、その抵抗器を流れる総電流またはその抵抗器の両端の電圧を計算でき、そこから、$ I ^ 2 R $または$ \ frac {V ^ 2}を使用してその抵抗器に供給される電力量を計算できます。 {R} $。