ネットワーク理論-2ポートネットワーク
一般に、入力変数と出力変数の関係を示す同等のモデルで表されている場合、電気ネットワークを分析するのは簡単です。このために、私たちは使用することができますtwo port network表現。名前が示すように、2つのポートネットワークには2つのポートが含まれています。このうち、一方のポートは入力ポートとして使用され、もう一方のポートは出力ポートとして使用されます。1番目と2番目のポートは、それぞれport1とport2と呼ばれます。
One port networkは2端子の電気ネットワークで、電流は1つの端子から入り、別の端子から出ます。抵抗、インダクタ、コンデンサは、それぞれに2つの端子があるため、1つのポートネットワークの例です。次の図に、1つのポートネットワーク表現を示します。
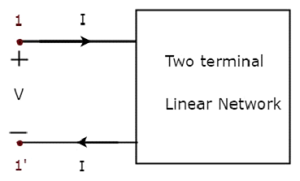
ここで、端子のペア1&1 'はポートを表します。この場合、1ポートネットワークであるため、ポートは1つだけです。
同様に、 two port networkは、2端子電気ネットワークのペアであり、電流は各ポートの1つの端子から入り、別の端子から出ます。次の図に、2ポートネットワークの表現を示します。
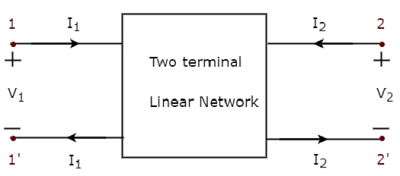
ここで、1対の端子1&1 'は1つのポートを表し、次のように呼ばれます。 port1 もう一方の端子のペアである2&2 'は、次のように呼ばれる別のポートを表します。 port2。
がある four variablesV 1、V 2、I 1及びI 2 2つのポートネットワークの図に示すように。そのうち、2つの変数を独立変数として選択し、別の2つの変数を従属変数として選択できます。したがって、6つの可能な方程式のペアを取得します。これらの方程式は、独立変数の観点から従属変数を表します。独立変数の係数は次のように呼ばれますparameters。したがって、方程式の各ペアは4つのパラメーターのセットを提供します。
2つのポートネットワークパラメータ
2ポートネットワークのパラメータは次のように呼ばれます two port network parametersまたは単に、2つのポートパラメータ。以下は、2つのポートネットワークパラメータのタイプです。
- Zパラメータ
- Yパラメータ
- Tパラメータ
- T 'パラメータ
- h-parameters
- g-parameters
ここで、これら2つのポートネットワークパラメータについて1つずつ説明します。
Zパラメータ
私たちは、変数V考慮することにより、2つの以下の式のセットを取得します1&V 2に依存し、私のように1&I 2の独立したとしてを。独立変数の係数は、I 1及びI 2は、と呼ばれていますZ parameters。
$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$
$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$
ザ・ Z parameters です
$$ Z_ {11} = \ frac {V_1} {I_1}、\:when \:I_2 = 0 $$
$$ Z_ {12} = \ frac {V_1} {I_2}、\:when \:I_1 = 0 $$
$$ Z_ {21} = \ frac {V_2} {I_1}、\:when \:I_2 = 0 $$
$$ Z_ {22} = \ frac {V_2} {I_2}、\:when \:I_1 = 0 $$
Zパラメータは次のように呼ばれます impedance parametersこれらは単に電圧と電流の比率だからです。Zパラメータの単位はオーム(Ω)です。
我々は2つのZパラメータ、Zを計算することができます11およびZ 21のポート2の開放を行うことによって、。同様に、我々は、他の2つのZパラメータ、Z計算することができる12およびZ 22のPORT1の開回路の操作を行って。したがって、Zパラメータは次のようにも呼ばれます。open-circuit impedance parameters。
Yパラメータ
私たちは、私の変数考慮して2つの以下の式のセットを取得します1&I 2依存などとV 1&V 2として独立を。独立変数の係数、V 1及びV 2は、と呼ばれていますY parameters。
$$ I_1 = Y_ {11} V_1 + Y_ {12} V_2 $$
$$ I_2 = Y_ {21} V_1 + Y_ {22} V_2 $$
ザ・ Y parameters です
$$ Y_ {11} = \ frac {I_1} {V_1}、\:\:V_2 = 0 $$の場合
$$ Y_ {12} = \ frac {I_1} {V_2}、\:\:V_1 = 0 $$の場合
$$ Y_ {21} = \ frac {I_2} {V_1}、\:\:V_2 = 0 $$の場合
$$ Y_ {22} = \ frac {I_2} {V_2}、\:\:V_1 = 0 $$の場合
Yパラメータは次のように呼ばれます admittance parametersこれらは単純に、電流と電圧の比率だからです。Yパラメータの単位はモーです。
我々は2つのYパラメータ、Yを計算することができます11及びY 21のポート2の短絡を行うことで。同様に、我々は、他の2つのYパラメーター、Y計算することができる12及びY 22のPORT1の短絡を行うことによって。したがって、Yパラメータは次のようにも呼ばれます。short-circuit admittance parameters。
Tパラメータ
私たちは、変数を考慮することにより、2つの以下の式のセットを取得しますV 1&I 1依存などとV 2&I 2を独立したとして。Vの係数2及び-I 2はと呼ばれT parameters。
$$ V_1 = A V_2-B I_2 $$
$$ I_1 = C V_2-D I_2 $$
ザ・ T parameters です
$$ A = \ frac {V_1} {V_2}、\:when \:I_2 = 0 $$
$$ B =-\ frac {V_1} {I_2}、\:when \:V_2 = 0 $$
$$ C = \ frac {I_1} {V_2}、\:when \:I_2 = 0 $$
$$ D =-\ frac {I_1} {I_2}、\:when \:V_2 = 0 $$
Tパラメータは送信パラメータまたは ABCD parameters。パラメータAとDは次元が少ないため、単位はありません。パラメータの単位BとCは、それぞれオームとモーです。
ポート2を開回路にすることで、AとCの2つのパラメータを計算できます。同様に、port2を短絡することにより、他の2つのパラメータBとDを計算できます。
T 'パラメータ
私たちは、変数V考慮することにより、2つの以下の式のセットを取得します2&I 2依存やVなど1&I 1として独立を。Vの係数1及び-I 1と呼ばれT’ parameters。
$$ V_2 = A'V_1-B 'I_1 $$
$$ I_2 = C'V_1-D 'I_1 $$
ザ・ T’ parameters です
$$ A '= \ frac {V_2} {V_1}、\:when \:I_1 = 0 $$
$$ B '=-\ frac {V_2} {I_1}、\:when \:V_1 = 0 $$
$$ C '= \ frac {I_2} {V_1}、\:when \:I_1 = 0 $$
$$ D '=-\ frac {I_2} {I_1}、\:when \:V_1 = 0 $$
T 'パラメータは逆伝送パラメータまたは A’B’C’D’ parameters。パラメータA 'とD'は次元が少ないため、単位はありません。パラメータの単位であるB 'とC'は、それぞれオームとモーです。
port1の開回路を実行することにより、2つのパラメーターA 'とC'を計算できます。同様に、port1を短絡することにより、他の2つのパラメーターB 'とD'を計算できます。
hパラメータ
私たちは、変数V考慮することにより、2つの以下の式のセットを取得します1&I 2依存とIとして1&V 2として独立を。独立変数の係数は、I 1及びV 2、と呼ばれていますh-parameters。
$$ V_1 = h_ {11} I_1 + h_ {12} V_2 $$
$$ I_2 = h_ {21} I_1 + h_ {22} V_2 $$
hパラメータは
$$ h_ {11} = \ frac {V_1} {I_1}、\:when \:V_2 = 0 $$
$$ h_ {12} = \ frac {V_1} {V_2}、\:when \:I_1 = 0 $$
$$ h_ {21} = \ frac {I_2} {I_1}、\:when \:V_2 = 0 $$
$$ h_ {22} = \ frac {I_2} {V_2}、\:when \:I_1 = 0 $$
hパラメータは次のように呼ばれます hybrid parameters。パラメータ、H 12及びH 21は、それらが寸法以下であるため、任意の単位を持っていません。パラメータの単位、H 11及びH 22は、それぞれ、オームとモーです。
我々は、2つのパラメータ、時間計算することができる11及びh 21をPORT2の短絡を行うことによって。同様に、我々は、他の2つのパラメータ、時間計算することができる12及びh 22をポート1の開回路の操作を行って。
hパラメータまたはハイブリッドパラメータは、トランジスタモデリング回路(ネットワーク)で役立ちます。
gパラメータ
私たちは、変数I考慮して2つの以下の式のセットを取得します1&V 2に依存するようにしてV 1&I 2の独立したとしてを。独立変数の係数、V 1及びI 2は、と呼ばれていますg-parameters。
$$ I_1 = g_ {11} V_1 + g_ {12} I_2 $$
$$ V_2 = g_ {21} V_1 + g_ {22} I_2 $$
ザ・ g-parameters です
$$ g_ {11} = \ frac {I_1} {V_1}、\:when \:I_2 = 0 $$
$$ g_ {12} = \ frac {I_1} {I_2}、\:when \:V_1 = 0 $$
$$ g_ {21} = \ frac {V_2} {V_1}、\:when \:I_2 = 0 $$
$$ g_ {22} = \ frac {V_2} {I_2}、\:\:V_1 = 0 $$の場合
gパラメータは次のように呼ばれます inverse hybrid parameters。パラメータは、G 12及びG 21は、それらが以下の寸法であるので、任意単位を有していません。パラメータの単位は、G 11及びG 22は、それぞれ、モーとオームです。
我々は2つのパラメータ、グラム計算することができ11とg 21のポート2の開放を行うことで。同様に、我々は、他の2つのパラメータ、G計算することができる12及びG 22をポート1の短絡を行うことによって。