ネットワーク理論-ネットワークトポロジ
ネットワークトポロジは、電気回路をグラフィカルに表現したものです。複雑な電気回路をネットワークグラフに変換して分析するのに便利です。ネットワークトポロジは、Graph theory。
ネットワークトポロジの基本的な用語
ここで、このネットワークトポロジに関連する基本的な用語について説明します。
グラフ
ネットワークグラフは単に次のように呼ばれます graph。これは、ブランチで接続されたノードのセットで構成されています。グラフでは、ノードは2つ以上のブランチの共通点です。場合によっては、単一のブランチのみがノードに接続することがあります。分岐は、2つのノードを接続する線分です。
任意の電気回路またはネットワークを同等のものに変換できます graph受動素子と電圧源を短絡に、電流源を開回路に置き換えることによって。つまり、グラフの線分は、受動素子または電気回路の電圧源のいずれかに対応する分岐を表しています。
例
次のことを考えてみましょう electric circuit。
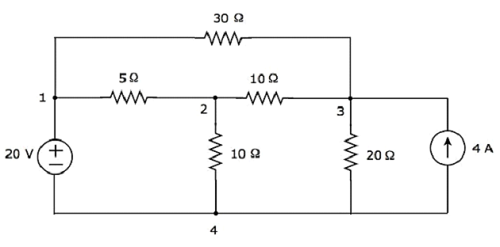
上記の回路には、 four principal nodes そしてそれらは1、2、3、および4でラベル付けされています。 seven branches 上記の回路では、1つのブランチに20 Vの電圧源が含まれ、別のブランチに4 Aの電流源が含まれ、残りの5つのブランチにはそれぞれ30Ω、5Ω、10Ω、10Ω、20Ωの抵抗が含まれています。
同等のもの graph 上記の電気回路に対応するものを下図に示します。
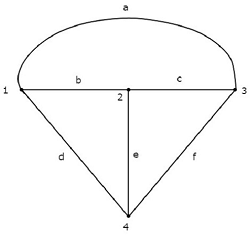
上のグラフには、 four nodesそしてそれらはそれぞれ1、2、3、4のラベルが付いています。これらは、電気回路の主要ノードのそれと同じです。があるsix branches 上のグラフでは、それらにはそれぞれa、b、c、d、e、fのラベルが付いています。
この場合、 one branch less 電気回路を同等のグラフに変換しながら、4A電流源を開回路として作成しているためです。
この例から、次の点を結論付けることができます-
ザ・ number of nodes グラフに存在するのは、電気回路に存在する主要ノードの数に等しくなります。
ザ・ number of branches グラフに存在するものは、電気回路に存在する分岐の数以下になります。
グラフの種類
グラフの種類は次のとおりです-
- コネクテッドグラフ
- 接続されていないグラフ
- 有向グラフ
- 無向グラフ
それでは、これらのグラフを1つずつ説明していきましょう。
コネクテッドグラフ
グラフの2つのノードのいずれかに少なくとも1つの分岐が存在する場合、それは connected graph。つまり、接続されたグラフの各ノードには、それに接続された1つ以上のブランチがあります。したがって、ノードが分離または分離された状態で表示されることはありません。
前の例に示されているグラフは connected graph。ここでは、すべてのノードが3つのブランチで接続されています。
接続されていないグラフ
グラフ内に単一のブランチでも接続されていないノードが少なくとも1つ存在する場合、それはと呼ばれます。 unconnected graph。したがって、接続されていないグラフには1つ以上の孤立したノードがあります。
次の図に示すグラフについて考えてみます。
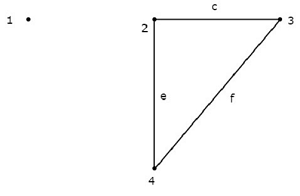
このグラフでは、ノード2、3、および4はそれぞれ2つのブランチで接続されています。しかし、1つのブランチでさえ接続されていませんnode 1。したがって、ノード1はisolated node。したがって、上のグラフはunconnected graph。
有向グラフ
グラフのすべてのブランチが矢印で表されている場合、そのグラフは directed graph。これらの矢印は、各ブランチの電流の方向を示しています。したがって、このグラフは次のようにも呼ばれます。oriented graph。
次の図に示すグラフについて考えてみます。
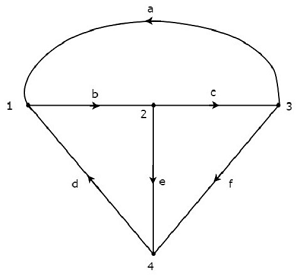
上のグラフでは、電流の流れの方向が各ブランチに矢印で表されています。したがって、それはdirected graph。
無向グラフ
グラフの分岐が矢印で表されていない場合、そのグラフは undirected graph。電流の方向がないため、このグラフはunoriented graph。
この章の最初の例で示したグラフは、 unoriented graph、そのグラフのブランチに矢印がないためです。
サブグラフとそのタイプ
グラフの一部は、 subgraph。特定のグラフのいくつかのノードやブランチを削除することでサブグラフを取得します。したがって、サブグラフのブランチやノードの数は、元のグラフの数よりも少なくなります。したがって、サブグラフはグラフのサブセットであると結論付けることができます。
以下は two types サブグラフの。
- Tree
- Co-Tree
木
ツリーは、特定のグラフの接続されたサブグラフであり、グラフのすべてのノードが含まれています。ただし、そのサブグラフにはループがあってはなりません。木の枝は次のように呼ばれますtwigs。
次のことを考慮してください connected subgraph この章の冒頭の例に示されているグラフの。
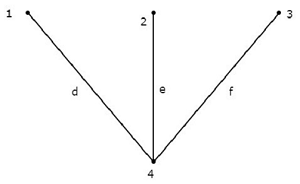
この接続されたサブグラフには、指定されたグラフの4つのノードすべてが含まれ、ループはありません。したがって、それはTree。
このツリーには、指定されたグラフの6つのブランチのうち3つのブランチしかありません。なぜなら、グラフの残りのブランチの1つのブランチでさえ考慮すると、上記の接続されたサブグラフにループが存在するからです。その場合、結果の接続されたサブグラフはツリーではなくなります。
上記のツリーから、次のように結論付けることができます。 number of branches ツリーに存在するものは、 n - 1 ここで、「n」は指定されたグラフのノードの数です。
コツリー
Co-Treeはサブグラフであり、ツリーの形成中に削除されたブランチで形成されます。したがって、それはとして呼ばれますComplement木の。すべてのツリーに対して、対応するCo-Treeがあり、そのブランチは次のように呼ばれます。linksまたは和音。通常、リンクは点線で表されます。
ザ・ Co-Tree 上記のツリーに対応するものを次の図に示します。
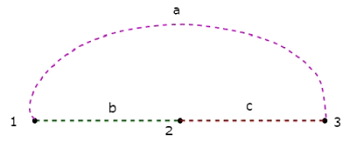
ノード4は上記のCo-Treeから分離されているため、このCo-Treeには、指定されたグラフの4つのノードではなく3つのノードしかありません。したがって、Co-Treeは接続されたサブグラフである必要はありません。このCo-Treeには3つのブランチがあり、それらはループを形成します。
ザ・ number of branchesコツリーに存在するものは、特定のグラフの枝の数と小枝の数の差に等しくなります。数学的には、次のように書くことができます
$$ l = b-(n-1)$$
$$ l = b-n + 1 $$
どこ、
- l リンクの数です。
- b 特定のグラフに存在するブランチの数です。
- n 特定のグラフに存在するノードの数です。
ツリーとそれに対応するCo-Treeを組み合わせると、次のようになります。 original graph 以下に示すように。
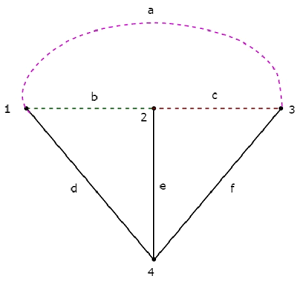
木の枝d、e、fは実線で表されます。Co-Treeブランチa、b、cは破線で表されます。