ネットワーク理論-DC回路の応答
入力用の電気回路の出力が時間に対して変化する場合、それは次のように呼ばれます。 time response。時間応答は、次の2つの部分で構成されます。
- 過渡応答
- 定常状態の応答
この章では、最初にこれら2つの応答について説明し、次にDC電圧源によって励起されたときの直列RL回路でこれら2つの応答を観察します。
過渡応答
電気回路に入力を加えた後、出力が定常状態に達するまでに一定の時間がかかります。したがって、出力は定常状態になるまで過渡状態になります。したがって、過渡状態の間の電気回路の応答は、transient response。
't'の値が大きい場合、過渡応答はゼロになります。理想的には、この「t」の値は無限大である必要があります。しかし、実際にはfive time constants 十分です。
トランジェントの有無
一時的なものは、 sudden change電気回路に適用される、および/またはスイッチング動作によるソース内。2つの可能な切り替えアクションがあります。それらは開閉スイッチです。
ザ・ transient 一部は not present電気回路またはネットワークの応答で、抵抗のみが含まれている場合。なぜならresistor 電圧と電流の量を調整する機能があります。
ザ・ transient part occurs 次のようなエネルギー貯蔵要素の存在による電気回路またはネットワークの応答 inductor and capacitor。それらの要素に蓄えられたエネルギーを即座に変えることができないからです。
インダクタの動作
切り替え動作がt = 0で行われると仮定します。Inductor current切り替え動作が発生しても、瞬時には変化しません。つまり、スイッチング動作直後のインダクタ電流の値は、スイッチング動作直前のインダクタ電流の値と同じになります。
数学的には、次のように表すことができます。
$$ i_L(0 ^ +)= i_L(0 ^-)$$
コンデンサの動作
ザ・ capacitor voltageスイッチング動作が発生しても、インダクタ電流のように瞬時に変化することはありません。つまり、スイッチング動作直後のコンデンサ電圧の値は、スイッチング動作直前のコンデンサ電圧の値と同じになります。
数学的には、次のように表すことができます。
$$ v_c(0 ^ +)= v_c(0 ^-)$$
定常状態の応答
't'の値が大きい場合に過渡応答がゼロ値になった後も残る時間応答の部分は、次のように知られています。 steady state response。これは、定常状態での応答に一時的な部分がないことを意味します。
インダクタの動作
独立した電源が、1つまたは複数のインダクタと抵抗(オプション)を備えた電気回路またはネットワークに長時間接続されている場合、その電気回路またはネットワークは定常状態にあると言われます。したがって、その電気回路のインダクタに蓄えられるエネルギーは最大で一定です。
数学的には、次のように表すことができます。
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ 最大値と定数
$ \ Rightarrow i_L = $ 最大および定数
したがって、インダクタは constant current source 定常状態で。
インダクタ両端の電圧は
$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$
したがって、インダクタは short circuit 定常状態で。
コンデンサの動作
独立した電源が、1つまたは複数のコンデンサと抵抗(オプション)を備えた電気回路またはネットワークに長時間接続されている場合、その電気回路またはネットワークは定常状態にあると言われます。したがって、その電気回路のコンデンサに蓄えられるエネルギーは最大で一定です。
数学的には、次のように表すことができます。
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ 最大値と定数
$ \ Rightarrow v_c = $最大および定数
したがって、コンデンサは constant voltage source 定常状態で。
コンデンサに流れる電流は
$$ i_c = C \ frac {dv_c} {dt} = 0A $$
したがって、コンデンサは open circuit 定常状態で。
シリーズRL回路の応答を見つける
次のことを考慮してください series RL circuit 図。
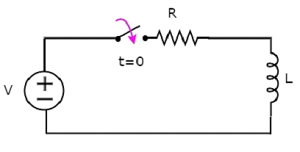
上記の回路では、 switch 保たれた opent = 0までで、t = 0で閉じられました。したがって、VボルトのDC電圧源は、この瞬間まで直列RL回路に接続されていません。したがって、no initial current インダクタを流れます。
回路図、 switch にあります closed 位置を次の図に示します。
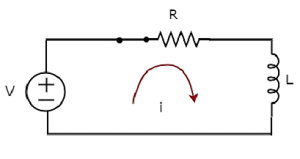
今、現在 i DC電圧源が持っているので、回路全体に流れます V ボルトは直列RL回路に接続されています。
今、適用します KVL ループの周り。
$$ V = Ri + L \ frac {di} {dt} $$
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
上記の方程式は一階微分方程式であり、次の形式になっています。
$ \ frac {dy} {dt} + Py = Q $Equation 2
沿って comparing 式1と式2では、次の関係が得られます。
$$ x = t $$
$$ y = i $$
$$ P = \ frac {R} {L} $$
$$ Q = \ frac {V} {L} $$
ザ・ solution 式2の
$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
どこ、 k は定数です。
式3のx、y、P、Qの値を代入します。
$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int(\ frac {V} {L})\ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {-\ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
回路には初期電流がないことがわかっています。したがって、t = 0および 定数の値を見つけるために式4で= 0 k。
$$ 0 = \ frac {V} {R} + ke ^ {-\ lgroup \ frac {R} {L} \ rgroup(0)} $$
$$ 0 = \ frac {V} {R} + k(1)$$
$$ k =-\ frac {V} {R} $$
式4のkの値を代入します。
$$ i = \ frac {V} {R} + \ lgroup- \ frac {V} {R} \ rgroup e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} $$
$$ i = \ frac {V} {R}-\ frac {V} {R} e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} $$
したがって、 current 回路を流れるのは
$ i =-\ frac {V} {R} e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
したがって、直列RL回路の応答は、DC電圧源によって励起された場合、次の2つの項があります。
最初の項$-\ frac {V} {R} e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} $は transient response。
2番目の項$ \ frac {V} {R} $は、 steady state response。これらの2つの応答を次の図に示します。
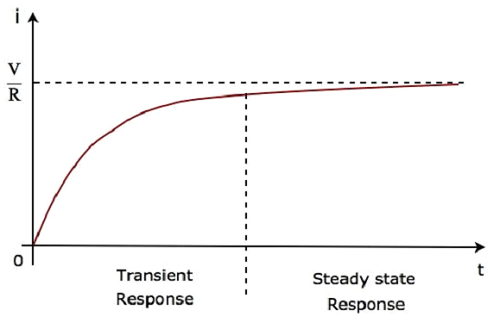
式5は次のように書き直すことができます。
$ i = \ frac {V} {R} \ lgroup 1-e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $
$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1-e ^ {-\ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6
どこ、 τ それは time constant その値は$ \ frac {L} {R} $に等しくなります。
式5と式6はどちらも同じです。しかし、式6から回路を流れる電流の上記の波形は、次のいくつかの値を代入することで簡単に理解できます。t 0、τ、2τ、5τなどのように。
上記の回路を流れる電流の波形では、過渡応答はゼロから最大5つの時定数を示しますが、定常状態の応答は5つの時定数以降を示します。