ネットワーク理論-クイックガイド

Network theory電気回路や電気ネットワークの問題を解決する研究です。この導入の章では、最初に電気回路の基本的な用語とネットワーク要素のタイプについて説明します。

基本的な用語

ネットワーク理論では、次の用語に頻繁に出くわします-

• 電気回路
• 電気ネットワーク
• Current
• Voltage
• Power

したがって、先に進む前に、これらの用語に関する基本的な知識を収集することが不可欠です。電気回路から始めましょう。

電気回路

電気回路には、電圧源または電流源からの電子の流れを提供するための閉じた経路が含まれています。電気回路に存在する要素はseries connection, parallel connection、または直列接続と並列接続の任意の組み合わせ。

電気ネットワーク

電気ネットワークは、電圧源または電流源からの電子の流れを提供するための閉じた経路を含む必要はない。したがって、「すべての電気回路は電気ネットワークである」と結論付けることができますが、その逆は真実である必要はありません。

電流

現在 "I"導体を通って流れることは、電荷の時間流量に他なりません。数学的には、次のように書くことができます

$$I = \frac{dQ}{dt}$$

どこ、

• Q は料金で、その単位はクーロンです。

• t は時間であり、その単位は秒です。

例えとして、電流はパイプを通る水の流れと考えることができます。電流は、Ampere。

一般に、 Electron current ソースの負の端子から正の端子に流れますが、 Conventional current ソースの正の端子から負の端子に流れます。

Electron current は自由電子の動きによって得られますが、 Conventional currentは、自由な正電荷の移動によって得られます。これらは両方ともelectric current。

電圧

電圧 "V"電荷（電子）を流す起電力に他なりません。数学的には、次のように書くことができます

$$V = \frac{dW}{dQ}$$

どこ、

• W は位置エネルギーであり、その単位はジュールです。

• Q は料金で、その単位はクーロンです。

例えとして、電圧は、水がパイプを通って流れる原因となる水の圧力と考えることができます。それはの観点から測定されますVolt。

力

パワー "P"電気エネルギーの時間流量に他なりません。数学的には、次のように書くことができます

$$P = \frac{dW}{dt}$$

どこ、

• W は電気エネルギーであり、 Joule。

• t は時間であり、秒単位で測定されます。

上記の式を書き直すことができます

$$P = \frac{dW}{dt} = \frac{dW}{dQ} \times \frac{dQ}{dt} = VI$$

したがって、 power に他なりません product 電圧の V そして現在 I。その単位はWatt。

ネットワーク要素の種類

いくつかのパラメータに基づいて、ネットワーク要素をさまざまなタイプに分類できます。ネットワーク要素の種類は次のとおりです-

• アクティブ要素とパッシブ要素

• 線形要素と非線形要素

• 二国間要素と片側要素

アクティブ要素とパッシブ要素

ネットワーク要素は次のいずれかに分類できます active または passive 電力を供給する能力に基づいています。

• Active Elements電気回路に存在する他の要素に電力を供給します。時々、それらは受動素子のように力を吸収するかもしれません。つまり、アクティブな要素には、電力の供給と吸収の両方の機能があります。Examples：電圧源と電流源。

• Passive Elements他の要素に電力（エネルギー）を供給することはできませんが、電力を吸収することはできます。つまり、これらの要素は、熱の形で電力を放散するか、磁場または電場の形でエネルギーを蓄積します。Examples：抵抗、インダクタ、およびコンデンサ。

線形要素と非線形要素

ネットワーク要素を次のように分類できます linear または non-linear 線形性の特性に従うという特性に基づいています。

• Linear Elements 電圧と電流の間に線形関係を示す要素です。 Examples：抵抗、インダクタ、およびコンデンサ。

• Non-Linear Elements 電圧と電流の間に線形関係を示さないものです。 Examples：電圧源と電流源。

二国間要素と片側要素

ネットワーク要素は、次のいずれかに分類することもできます。 bilateral または unilateral ネットワーク要素を流れる電流の方向に基づいています。

Bilateral Elements は、両方向の電流を許容し、電流のどちらの方向にも同じインピーダンスを提供する要素です。 Examples：抵抗、インダクタ、コンデンサ。

二国間要素の概念を次の図に示します。

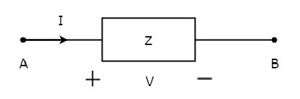
上記の図では、電流（I）を、受動素子を有するインピーダンスを介してBに端末Aから流入されるZ Ω。これは、端子AとBと電流（I）の間のその要素の両端の電圧（V）の比率です。

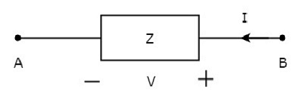
上記の図では、電流（I）を、受動素子を有するインピーダンスを介してAに端末Bから流入されるZ Ω。つまり、電流（–I）が端子AからBに流れています。この場合も、電流と電圧の両方が端子AとBに対して負の符号を持っているため、同じインピーダンス値が得られます。

Unilateral Elements一方向にのみ電流を流すことができるものです。したがって、それらは両方向で異なるインピーダンスを提供します。

前の章でネットワーク要素のタイプについて説明しました。それでは、nature of network elements 次の例に示すVI特性から。

例1

ザ・ V-I characteristics ネットワーク要素の概要を以下に示します。

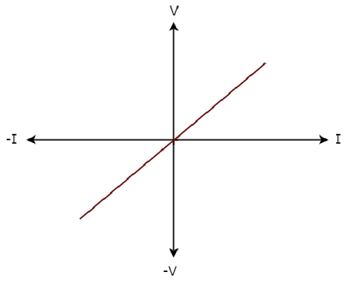
Step 1 −ネットワーク要素を次のように検証する linear または non-linear。

上図から、ネットワーク要素のVI特性は、原点を通る直線です。したがって、それはLinear element。

Step 2 −ネットワーク要素を次のように検証する active または passive。

ネットワーク要素の特定のVI特性は、第1象限と第3象限にあります。

• の中に first quadrant、電圧（V）と電流（I）の両方の値は正です。したがって、電圧（V）と電流（I）の比率は、正のインピーダンス値を示します。

• 同様に、 third quadrant、電圧（V）と電流（I）の両方の値が負の値になります。したがって、電圧（V）と電流（I）の比率は、正のインピーダンス値を生成します。

与えられたVI特性は正のインピーダンス値を提供するため、ネットワーク要素は Passive element。

Step 3 −ネットワーク要素を次のように検証する bilateral または unilateral。

特性上のすべての点（I、V）に対して、特定の特性上の対応する点（-I、-V）が存在します。したがって、ネットワーク要素はBilateral element。

したがって、与えられたVI特性は、ネットワーク要素が Linear, Passive、および Bilateral element。

例2

ザ・ V-I characteristics ネットワーク要素の概要を以下に示します。

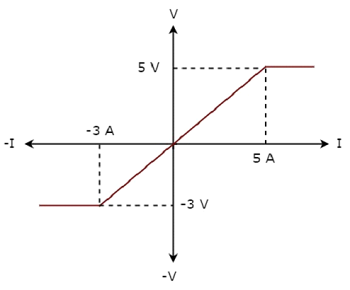
Step 1 −ネットワーク要素を次のように検証する linear または non-linear。

上図から、ネットワーク要素のVI特性は、ポイント（-3A、-3V）と（5A、5V）の間のみの直線です。これらの点を超えると、VI特性は線形関係に従いません。したがって、それはNon-linear element。

Step 2 −ネットワーク要素を次のように検証する active または passive。

ネットワーク要素の特定のVI特性は、第1象限と第3象限にあります。これらの2つの象限では、電圧（V）と電流（I）の比率によって正のインピーダンス値が生成されます。したがって、ネットワーク要素はPassive element。

Step 3 −ネットワーク要素を次のように検証する bilateral or unilateral。

特性上のポイント（5A、5V）を考慮してください。対応するポイント（-5A、-3V）は、（-5A、-5V）の代わりに、指定された特性上に存在します。したがって、ネットワーク要素はUnilateral element。

したがって、与えられたVI特性は、ネットワーク要素が Non-linear, Passive、および Unilateral element。

Active Elements電気回路に存在する他の要素に電力を供給するネットワーク要素です。したがって、アクティブな要素は、電圧または電流タイプのソースとも呼ばれます。これらのソースは、次の2つのカテゴリに分類できます-

• 独立した情報源
• 依存ソース

独立した情報源

名前が示すように、独立したソースは電圧または電流の固定値を生成し、これらは他のパラメータに依存しません。独立した情報源は、さらに次の2つのカテゴリに分類できます-

• 独立した電圧源
• 独立した電流源

独立した電圧源

独立した電圧源は、2つの端子間に一定の電圧を生成します。この電圧は、電圧源の2つの端子を流れる電流の量とは無関係です。

独立 ideal voltage source そのVI特性を次の図に示します。

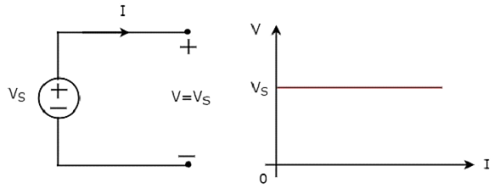
ザ・ V-I characteristics独立した理想的な電圧源のは一定の線であり、電流値（I）に関係なく、常に電源電圧（VS）に等しくなります。したがって、独立した理想的な電圧源の内部抵抗はゼロオームです。

したがって、独立した理想的な電圧源 do not exist practically、内部抵抗があるためです。

独立 practical voltage source そのVI特性を次の図に示します。

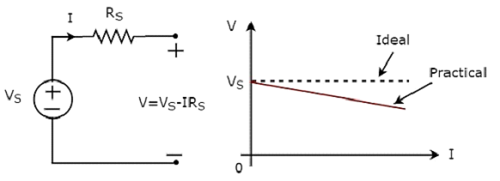
独立した実用的な電圧源のVI特性は、独立した理想的な電圧源のVI特性とは異なります。これは、独立した実用的な電圧源の内部抵抗（R _S）の両端の電圧降下によるものです。

独立した電流源

独立した電流源は定電流を生成します。この電流は、2つの端子間の電圧とは無関係です。独立ideal current source そのVI特性を次の図に示します。

ザ・ V-I characteristics独立した理想的な電流源のは一定の線であり、電圧値（V）に関係なく、常にソース電流（I _S）に等しくなります。したがって、独立した理想的な電流源の内部抵抗は無限オームです。

したがって、独立した理想的な電流源 do not exist practically、内部抵抗があるためです。

独立 practical current source そのVI特性を次の図に示します。

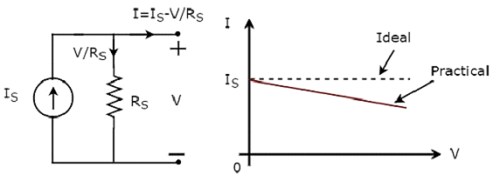
独立した実用的な電流源のVI特性には、独立した理想的な電流源のVI特性との偏差があります。これは、独立した実用的な電流源の内部シャント抵抗（R _S）を流れる電流の量によるものです。

依存ソース

名前が示すように、依存ソースは、他の電圧または電流に依存する量の電圧または電流を生成します。依存ソースは、controlled sources。依存ソースはさらに次の2つのカテゴリに分類できます-

• 依存電圧源
• 依存電流源

依存電圧源

従属電圧源は、2つの端子間に電圧を生成します。この電圧の量は、他の電圧または電流に依存します。したがって、従属電圧源はさらに次の2つのカテゴリに分類できます。

• 電圧依存電圧源（VDVS）
• 電流依存電圧源（CDVS）

依存電圧源は、ひし形の内側に「+」と「-」の記号で表されます。電圧源の大きさは、ひし形の外側で表すことができます。

依存電流源

従属電流源は電流を生成します。この電流の量は、他の電圧または電流に依存します。したがって、従属電流源はさらに次の2つのカテゴリに分類できます。

• 電圧依存電流源（VDCS）
• 電流依存電流源（CDCS）

依存電流源は、ひし形の内側に矢印で表されます。電流源の大きさは、ひし形の外側で表すことができます。

トランジスタの同等のモデルで、これらの依存ソースまたは制御ソースを観察できます。

ソース変換テクニック

私たちは、2つの実用的な情報源があることを知っています。 voltage source そして current source。ネットワークの問題を解決しながら、要件に基づいて1つのソースを別のソースに変換（変換）できます。

あるソースを別のソースに変換する手法は、次のように呼ばれます。 source transformation technique。以下は、2つの可能なソース変換です-

• 実用的な電圧源から実用的な電流源へ
• 実用的な電流源から実用的な電圧源へ

実用的な電圧源から実用的な電流源へ

実用的な電圧源から実用的な電流源への変換を次の図に示します。

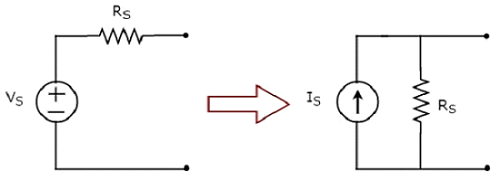
Practical voltage source抵抗（R _S）と直列の電圧源（V _S）で構成されます。これは、図に示すように、実用的な電流源に変換できます。これは、抵抗（R _S）と並列の電流源（I _S）で構成されています。

ISの値は、Vの比に等しくなる_S及びR _S。数学的には、次のように表すことができます。

$$I_S = \frac{V_S}{R_S}$$

実用的な電流源から実用的な電圧源へ

実用的な電流源から実用的な電圧源への変換を次の図に示します。

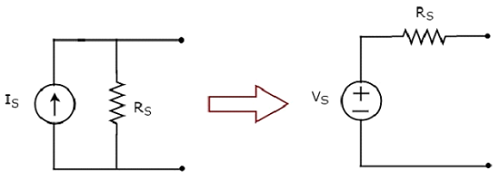
実用的な電流源は、抵抗（R _S）と並列の電流源（I _S）で構成されます。これは、図に示すように、実用的な電圧源に変換できます。これは、抵抗（R _S）と直列の電圧源（V _S）で構成されています。

Vの値_Sは、 Iの積に等しくなる_S及びR _S。数学的には、次のように表すことができます。

$$V_S = I_S R_S$$

この章では、抵抗、インダクタ、コンデンサなどの受動素子について詳しく説明します。抵抗器から始めましょう。

抵抗器

抵抗器の主な機能は、電流の流れに対抗するか制限することです。したがって、抵抗は、電流の量および/または分割（共有）電圧を制限するために使用されます。

抵抗器を流れる電流を1アンペア、両端の電圧をVボルトとします。ザ・symbol 次の図に、抵抗器と電流Iおよび電圧Vを示します。

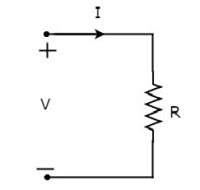
による Ohm’s law、抵抗器の両端の電圧は、抵抗器を流れる電流とその抵抗器の抵抗の積です。 Mathematically、次のように表すことができます

$V = IR$ Equation 1

$\Rightarrow I = \frac{V}{R}$Equation 2

どこ、 R は抵抗器の抵抗です。

式2から、抵抗を流れる電流は抵抗の両端に印加される電圧に正比例し、抵抗の抵抗に反比例すると結論付けることができます。

Power 電気回路要素では、次のように表すことができます

$P = VI$Equation 3

式3の式1を代入します。

$P = (IR)I$

$\Rightarrow P = I^2 R$ Equation 4

式3の式2を代入します。

$P = V \lgroup \frac{V}{R} \rgroup$

$\Rightarrow P = \frac{V^2}{R}$ Equation 5

したがって、式3〜5に記載されている式のいずれかを使用して、抵抗で消費される電力量を計算できます。

インダクタ

一般に、インダクタには巻数があります。したがって、電流が流れると磁束が発生します。したがって、インダクタによって生成される総磁束の量は電流に依存し、私はインダクタを流れ、それらは線形関係にあります。

Mathematically、次のように書くことができます

$$\Psi \: \alpha \: I$$

$$\Rightarrow \Psi = LI$$

どこ、

• Ψ は総磁束です

• L インダクタのインダクタンスです

インダクタを流れる電流を1アンペア、両端の電圧をVボルトとします。ザ・symbol次の図に、インダクタの電流Iと電圧Vを示します。

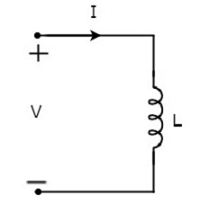
による Faraday’s law、インダクタ両端の電圧は次のように書くことができます。

$$V = \frac{d\Psi}{dt}$$

置換Ψ= LIを上記式に。

$$V = \frac{d(LI)}{dt}$$

$$\Rightarrow V = L \frac{dI}{dt}$$

$$\Rightarrow I = \frac{1}{L} \int V dt$$

上記の式から、次の式が存在すると結論付けることができます。 linear relationship インダクタ両端の電圧とインダクタを流れる電流の間。

私達はことを知っています power 電気回路要素では、次のように表すことができます

$$P = VI$$

代替 $V = L \frac{dI}{dt}$ 上記の式で。

$$P = \lgroup L \frac{dI}{dt}\rgroup I$$

$$\Rightarrow P = LI \frac{dI}{dt}$$

上記の式を積分することにより、次の式が得られます。 energy としてインダクタに格納されます

$$W = \frac{1}{2} LI^2$$

したがって、インダクタはエネルギーを磁場の形で蓄積します。

コンデンサ

一般に、コンデンサには、誘電体媒体によって分離された2つの導電性プレートがあります。コンデンサの両端に正の電圧が印加されると、正の電荷が蓄積されます。同様に、コンデンサの両端に負の電圧が印加されると、負の電荷が蓄積されます。

したがって、コンデンサに蓄積される電荷​​の量は、印加電圧に依存します Vそれを横切って、彼らは線形関係を持っています。数学的には、次のように書くことができます

$$Q \: \alpha \: V$$

$$\Rightarrow Q = CV$$

どこ、

• Q はコンデンサに蓄積された電荷です。

• C はコンデンサの静電容量です。

コンデンサを流れる電流を1アンペア、両端の電圧をVボルトとします。次の図に、コンデンサの記号と電流Iおよび電圧Vを示します。

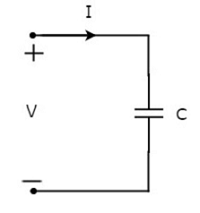
私たちは、 current に他なりません time rate of flow of charge。数学的には、次のように表すことができます。

$$I = \frac{dQ}{dt}$$

代替 $Q = CV$ 上記の式で。

$$I = \frac{d(CV)}{dt}$$

$$\Rightarrow I = C \frac{dV}{dt}$$

$$\Rightarrow V = \frac{1}{C} \int I dt$$

上記の式から、次の式が存在すると結論付けることができます。 linear relationship コンデンサ両端の電圧とコンデンサを流れる電流の間。

私達はことを知っています power 電気回路要素では、次のように表すことができます

$$P = VI$$

代替 $I = C \frac{dV}{dt}$ 上記の式で。

$$P = V \lgroup C \frac{dV}{dt} \rgroup$$

$$\Rightarrow P = CV \frac{dV}{dt}$$

上記の式を積分することにより、次の式が得られます。 energy としてコンデンサに格納されます

$$W = \frac{1}{2}CV^2$$

したがって、コンデンサは電界の形でエネルギーを蓄えます。

ネットワーク要素は、次のいずれかになります。 active または passiveタイプ。電気回路またはネットワークには、これら2種類のネットワーク要素のいずれかまたは両方の組み合わせが含まれています。

それでは、一般に次の2つの法則について説明します。 Kirchhoff’s laws。

• キルヒホッフの現行法
• キルヒホッフの電圧法則

キルヒホッフの現行法

キルヒホッフの電流法則（KCL）は、ノードを出る（または入る）電流の代数和はゼロに等しいと述べています。

A Node2つ以上の回路要素が接続されているポイントです。1つのノードに2つの回路要素のみが接続されている場合、それは単純ノードと呼ばれます。3つ以上の回路要素がノードに接続されている場合、それはPrincipal Node。

Mathematically、KCLは次のように表すことができます

$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$

どこ、

• I_mノードを出るm^番目の分岐電流です。

• M ノードに接続されているブランチの数です。

上記のステートメント KCL「ノードに入る電流の代数和は、ノードから出る電流の代数和に等しい」と表現することもできます。次の例でこのステートメントを確認しましょう。

例

書く KCL equation ノードで P 次の図の。

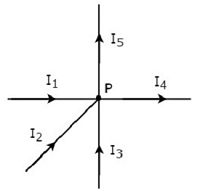
• 上の図では、分岐電流I ₁、I ₂とI _3がありますentering ノードPで。したがって、これら3つの電流の負の符号を考慮してください。

• 上の図で、枝電流I ₄とI ₅ですleaving ノードPから。したがって、これら2つの電流の正の符号を考慮してください。

ザ・ KCL equation ノードPで

$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$

$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$

上記の式で、左辺は流入電流の合計を表し、右辺は流出電流の合計を表します。

このチュートリアルでは、電流がノードを離れるときは正の符号を、ノードに入るときは負の符号を検討します。同様に、電流がノードを離れるときは負の符号を、ノードに入るときは正の符号を考慮することができます。どちらの場合も、result will be same。

Note − KCLは、ノードに接続されているネットワーク要素の性質に依存しません。

キルヒホッフの電圧法則

キルヒホッフの電圧法則（KVL）は、ループまたはメッシュの周りの電圧の代数和がゼロに等しいと述べています。

A Loopは、開始元と同じノードで終了するパスです。対照的に、Mesh は、内部に他のループを含まないループです。

数学的には、KVLは次のように表すことができます。

$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$

どこ、

• V_nループ（メッシュ）内のn^番目の要素の電圧です。

• N ループ（メッシュ）内のネットワーク要素の数です。

上記のステートメント KVL「電圧源の代数和は、ループ内に存在する電圧降下の代数和に等しい」と表現することもできます。次の例を使用して、このステートメントを確認しましょう。

例

書く KVL equation 次の回路のループの周り。

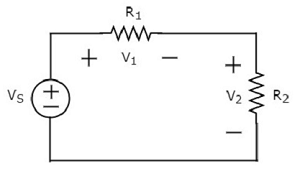
上記の回路図は、電圧源Vから成る_S二つの抵抗をRと直列に₁及びR ₂。抵抗Rの両端の電圧は降下₁及びR _2がVである₁及びV ₂はそれぞれ。

適用する KVL ループの周り。

$$V_S - V_1 - V_2 = 0$$

$$\Rightarrow V_S = V_1 + V_2$$

上記の式で、左辺の項は単一の電圧源VSを表します。一方、右側はsum of voltage drops。この例では、1つの電圧源のみを考慮しました。そのため、左側には1つの用語しか含まれていません。複数の電圧源を検討する場合、左側には電圧源の合計が含まれます。

このチュートリアルでは、各要素の電圧の符号を、ループ内を移動するときに存在する2番目の端子の極性と見なします。同様に、各電圧の符号は、ループを移動しているときに存在する最初の端子の極性と見なすことができます。どちらの場合も、result will be same。

Note − KVLは、ループ内に存在するネットワーク要素の性質に依存しません。

この章では、電気量の次の2つの分割原理について説明します。

• 現在の分割原則
• 分圧原理

現在の分割原則

2つ以上の受動素子が並列に接続されている場合、各素子を流れる電流の量は divided （共有）ノードに流入している電流からそれらの間で。

次のことを考慮してください circuit diagram。

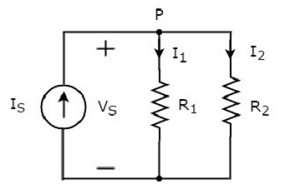
上記の回路図は、入力電流源で構成されています I_S 2つの抵抗器と並列 R₁ そして R₂。各要素の両端の電圧はV_S。抵抗器を流れる電流R₁ そして R₂ です I₁ そして I₂ それぞれ。

ザ・ KCL equation ノードで P になります

$$I_S = I_1 + I_2$$

• 代替 $I_1 = \frac{V_S}{R_1}$ そして $I_2 = \frac{V_S}{R_2}$ 上記の式で。

$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} = V_S \lgroup \frac {R_2 + R_1 }{R_1 R_2} \rgroup$$

$$\Rightarrow V_S = I_S \lgroup \frac{R_1R_2}{R_1 + R_2} \rgroup$$

• 値が代入V _Sでの$I_1 = \frac{V_S}{R_1}$。

$$I_1 = \frac{I_S}{R_1}\lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$

$$\Rightarrow I_1 = I_S\lgroup \frac{R_2}{R_1 + R_2} \rgroup$$

• 値が代入V _Sでの$I_2 = \frac{V_S}{R_2}$。

$$I_2 = \frac{I_S}{R_2} \lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$

$$\Rightarrow I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$

式からI ₁及びI ₂、我々は、任意の受動素子に流れる電流は以下の式を用いて求めることができることを一般化することができます。

$$I_N = I_S \lgroup \frac{Z_1\rVert Z_2 \rVert...\rVert Z_{N-1}}{Z_1 + Z_2 + ... + Z_N}\rgroup$$

これはとして知られています current division principle また、2つ以上の受動素子が並列に接続され、1つの電流のみがノードに流入する場合に適用できます。

どこ、

• I _Nは、N^番目の分岐の受動素子を流れる電流です。

• I _Sは、ノードに入る入力電流です。

• Z ₁、Z ₂、...、Z _Nは、 1つのインピーダンスです^番目の支店、2^回目のブランチ、...、N^番目のそれぞれのブランチは。

分圧原理

2つ以上の受動素子が直列に接続されている場合、各素子の両端に存在する電圧の量は divided （共有）その組み合わせ全体で利用可能な電圧からそれらの間で。

次のことを考慮してください circuit diagram。

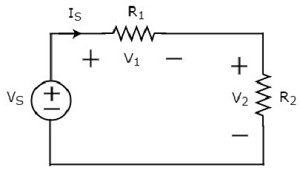
上記の回路図は、電圧源Vから成る_S二つの抵抗をRと直列に₁及びR ₂。これらの要素を流れる電流は_ISです。抵抗Rの両端の電圧は降下₁及びR _2がVである₁及びV ₂はそれぞれ。

ザ・ KVL equation ループの周りは

$$V_S = V_1 + V_2$$

• 代替V ₁ = I _S R ₁およびV ₂ = I _S R ₂上記式

$$V_S = I_S R_1 + I_S R_2 = I_S(R_1 + R_2)$$

$$I_S = \frac{V_S}{R_1 + R_2}$$

• 値を代入I _Sを中V ₁ = I _S R ₁。

$$V_1 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_1$$

$$\Rightarrow V_1 = V_S \lgroup \frac {R_1}{R_1 + R_2} \rgroup$$

• 値を代入I _SのにV ₂ = I _S R ₂。

$$V_2 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_2$$

$$\Rightarrow V_2 = V_S \lgroup \frac {R_2}{R_1 + R_2} \rgroup$$

式からV ₁及びV ₂、我々は、任意の受動素子の両端の電圧は以下の式を用いて求めることができることを一般化することができます。

$$V_N = V_S \lgroup \frac {Z_N}{Z_1 + Z_2 +....+ Z_N}\rgroup$$

これはとして知られています voltage division principle また、2つ以上の受動素子が直列に接続されており、組み合わせ全体で1つの電圧しか使用できない場合に適用できます。

どこ、

• V _Nは、N^番目の受動素子の両端の電圧です。

• V _Sは入力電圧であり、直列受動素子の組み合わせ全体に存在します。

• Z ₁、Z ₂、...、Z _3が1つのインピーダンスである^番目の受動素子、2^番目の受動素子、...、N^番目のそれぞれの受動素子。

電気ネットワークを解決するために使用される2つの基本的な方法があります。 Nodal analysis そして Mesh analysis。この章では、Nodal analysis 方法。

節点解析では、接地に対する節点電圧を考慮します。したがって、節点解析は次のようにも呼ばれます。Node-voltage method。

節点解析の手順

節点解析を使用して電気ネットワークまたは回路を解きながら、次の手順に従います。

• Step 1 −特定する principal nodes そのうちの1つを選択します reference node。その参照ノードをグラウンドとして扱います。

• Step 2 −ラベルを付ける node voltages 参照ノードを除くすべての主要ノードからのグラウンドに関して。

• Step 3 −書く nodal equations参照ノードを除くすべての主要ノード。節点方程式は、最初にKCLを適用し、次にオームの法則を適用することによって得られます。

• Step 4 −ノード電圧を取得するために、ステップ3で取得したノード方程式を解きます。

これで、ノード電圧を使用して、任意の要素を流れる電流と、特定のネットワークに存在する任意の要素の両端の電圧を見つけることができます。

例

次の回路の20Ω抵抗を流れる電流を Nodal analysis。

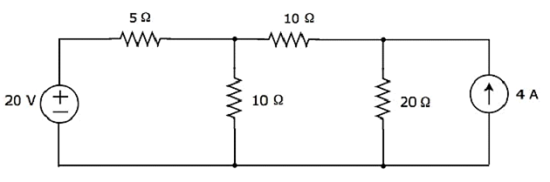
Step 1 −あります three principle nodes上記の回路で。次の図では、これらに1、2、および3のラベルが付いています。

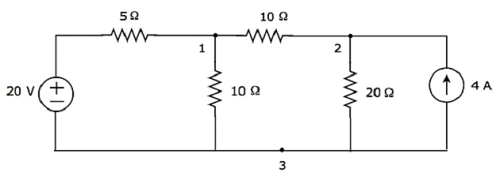
上の図では、 node 3 参照ノード（グラウンド）として。

Step 2-ノード電圧、V ₁及びV _2は、以下の図に標識されます。

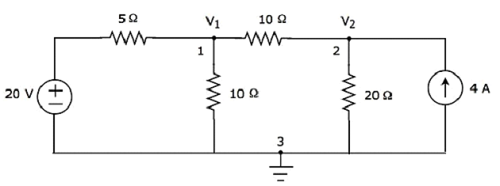
上記の図では、V _1が地面に対してノード1からの電圧であり、V _2は、地面に対して、ノード2からの電圧です。

Step 3 −この場合、 two nodal equations、Ground以外に2つの主要ノード1と2があるため。ノードで節点方程式を書くとき、すべての電流が電流の方向が言及されていないノードから出ており、そのノードの電圧が回路内の他のノード電圧よりも大きいと仮定します。

ザ・ nodal equation ノード1には

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1 - V_2}{10} = 0$$

$$\Rightarrow \frac{2 V_1 - 40 + V_1 + V_1 - V_2}{10} = 0$$

$$\Rightarrow 4V_1 - 40 - V_2 = 0$$

$\Rightarrow V_2 = 4V_1 - 40$ Equation 1

ザ・ nodal equation ノード2には

$$-4 + \frac{V_2}{20} + \frac{V_2 - V_1}{10} = 0$$

$$\Rightarrow \frac{-80 + V_2 + 2V_2 - 2V_2}{20} = 0$$

$\Rightarrow 3V_2 − 2V_1 = 80$ Equation 2

Step 4-発見ノード電圧、V ₁及びV ₂式1及び式2を解くことによって。

式1を式2に代入します。

$$3(4 V_1 - 40) - 2 V_1 = 80$$

$$\Rightarrow 12 V_1 - 120 - 2V_1 =80$$

$$\Rightarrow 10 V_1 = 200$$

$$\Rightarrow V_1 = 20V$$

式_1にV1 = 20Vを代入します。

$$V_2 = 4(20) - 40$$

$$\Rightarrow V_2 = 40V$$

そこで、我々は、ノードが電圧しまっV ₁及びV ₂として、20 V そして 40 V それぞれ。

Step 5−20Ω抵抗の両端の電圧はノード電圧V _2に他ならず、40 Vに等しくなります。これで、オームの法則を使用して、20Ω抵抗を流れる電流を見つけることができます。

$$I_{20 \Omega} = \frac{V_2}{R}$$

値を代入しV ₂上式であり、Rが。

$$I_{20 \Omega} = \frac{40}{20}$$

$$\Rightarrow I_{20 \Omega} = 2A$$

したがって、特定の回路の20Ω抵抗を流れる電流は次のようになります。 2 A。

Note−上記の例から、電気回路に「n」個の主ノード（参照ノードを除く）がある場合、「n」個の節点方程式を解く必要があると結論付けることができます。したがって、次の場合に節点解析を選択できます。number of principal nodes （参照ノードを除く）は、電気回路のメッシュ数よりも少ないです。

メッシュ解析では、各メッシュを流れる電流を考慮します。したがって、メッシュ分析は次のようにも呼ばれます。Mesh-current method。

A branchは2つのノードを結合するパスであり、回路要素が含まれています。ブランチが1つのメッシュのみに属している場合、ブランチ電流はメッシュ電流に等しくなります。

分岐が2つのメッシュに共通である場合、分岐電流は、同じ（または反対の）方向にある場合、2つのメッシュ電流の合計（または差）に等しくなります。

メッシュ解析の手順

メッシュ分析を使用して電気ネットワークまたは回路を解決するときは、次の手順に従ってください。

• Step 1 −特定する meshes メッシュ電流に時計回りまたは反時計回りのいずれかの方向にラベルを付けます。

• Step 2 −メッシュ電流の観点から各要素を流れる電流の量を観察します。

• Step 3 −書く mesh equationsすべてのメッシュに。メッシュ方程式は、最初にKVLを適用し、次にオームの法則を適用することによって得られます。

• Step 4 −ステップ3で得られたメッシュ方程式を解いて、 mesh currents。

これで、メッシュ電流を使用して、任意の要素を流れる電流と、特定のネットワークに存在する任意の要素の両端の電圧を見つけることができます。

例

を使用して30Ω抵抗の両端の電圧を見つけます Mesh analysis。

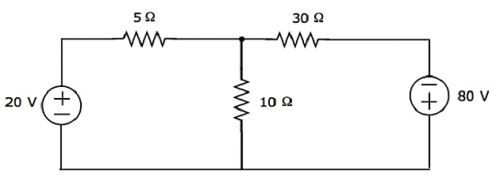
Step 1−上記の回路には2つのメッシュがあります。ザ・mesh currentsI ₁及びI _2は時計方向に考慮されます。これらのメッシュ電流を次の図に示します。

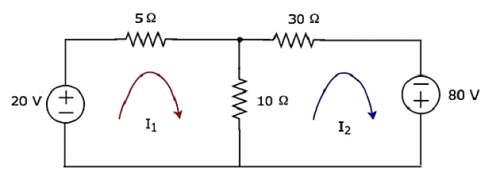
Step 2−メッシュ電流I ₁は、20Vの電圧源と5Ωの抵抗を流れます。同様に、メッシュ電流I ₂は、30Ωの抵抗と-80Vの電圧源を流れます。しかし、2つのメッシュ電流の差は、I ₁及びI _2は、それが2つのメッシュの共通の枝であることから、10Ωの抵抗を介して流れます。

Step 3 −この場合、 two mesh equations与えられた回路には2つのメッシュがあるからです。メッシュ方程式を書くとき、その特定のメッシュのメッシュ電流が回路の他のすべてのメッシュ電流よりも大きいと仮定します。

ザ・ mesh equation 最初のメッシュの

$$20 - 5I_1 -10(I_1 - I_2) = 0$$

$$\Rightarrow 20 - 15I_1 + 10I_2 = 0$$

$$\Rightarrow 10I_2 = 15I_1 - 20$$

上記の式を5で割ります。

$$2I_2 = 3I_1 - 4$$

上記の式に2を掛けます。

$4I_2 = 6I_1 - 8$ Equation 1

ザ・ mesh equation 2番目のメッシュの

$$-10(I_2 - I_1) - 30I_2 + 80 = 0$$

上記の式を10で割ります。

$$-(I_2 - I_1) - 3I_2 + 8 = 0$$

$$\Rightarrow -4I_2 + I_1 + 8 = 0$$

$4I_2 = I_1 + 8$ Equation 2

Step 4-検索では、電流をメッシュI ₁とI ₂式1と式2を解くことによって。

式1と式2の左辺の項は同じです。したがって、I _1の値を見つけるために、式1と式2の右辺の項を等しくします。

$$6I_1 - 8 = I_1 + 8$$

$$\Rightarrow 5I_1 = 16$$

$$\Rightarrow I_1 = \frac{16}{5} A$$

置き換えI _1つの、式2の値を。

$$4I_2 = \frac{16}{5} + 8$$

$$\Rightarrow 4I_2 = \frac{56}{5}$$

$$\Rightarrow I_2 = \frac{14}{5} A$$

そこで、我々は、メッシュ電流を得たI ₁とI ₂など$\mathbf{\frac{16}{5}}$ A そして $\mathbf{\frac{14}{5}}$ A それぞれ。

Step 5−30Ωの抵抗を流れる電流はメッシュ電流I _2に他ならず、次のようになります。$\frac{14}{5}$ A.これで、オームの法則を使用して、30Ωの抵抗の両端の電圧を見つけることができます。

$$V_{30 \Omega} = I_2 R$$

値を代入I ₂及びRが上記式。

$$V_{30 \Omega} = \lgroup \frac{14}{5} \rgroup 30$$

$$\Rightarrow V_{30 \Omega} = 84V$$

したがって、特定の回路の30Ω抵抗の両端の電圧は次のようになります。 84 V。

Note 1−上記の例から、電気回路に「m」メッシュがある場合、「m」メッシュ方程式を解く必要があると結論付けることができます。そのため、メッシュの数が電気回路の主要ノード（参照ノードを除く）の数よりも少ない場合に、メッシュ分析を選択できます。

Note 2 −メッシュの数が任意の電気回路の主ノード（参照ノードを除く）の数と等しい場合、ノード解析またはメッシュ解析のいずれかを選択できます。

回路が2つ以上の類似した受動素子で構成され、直列タイプまたは並列タイプのみで接続されている場合、それらを1つの同等の受動素子に置き換えることができます。したがって、この回路はequivalent circuit。

この章では、次の2つの等価回路について説明します。

• 直列等価回路
• 並列等価回路

直列等価回路

同様の受動素子が接続されている場合 seriesの場合、これらすべての要素に同じ電流が流れます。ただし、電圧は各要素で分割されます。

次のことを考慮してください circuit diagram。

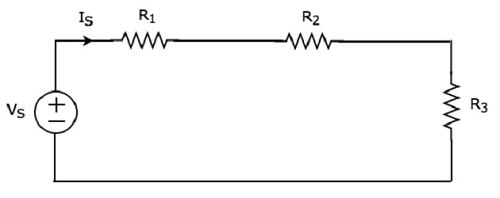
これは、単一の電圧源（V有し_S）とRの抵抗値を有する3つの抵抗₁、R ₂及びR _3は。これらの要素はすべて直列に接続されています。現在のISは、これらすべての要素を流れます。

上記の回路にはメッシュが1つしかありません。ザ・KVL equation このメッシュの周りは

$$V_S = V_1 + V_2 + V_3$$

代替 $V_1 = I_S R_1, \: V_2 = I_S R_2$ そして $V_3 = I_S R_3$ 上記の式で。

$$V_S = I_S R_1 + I_S R_2 + I_S R_3$$

$$\Rightarrow V_S = I_S(R_1 + R_2 + R_3)$$

上記の式は次の形式です。 $V_S = I_S R_{Eq}$ どこ、

$$R_{Eq} = R_1 + R_2 + R_3$$

ザ・ equivalent circuit diagram 与えられた回路のは次の図に示されています。

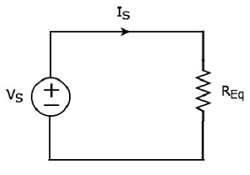
つまり、複数の抵抗器が直列に接続されている場合、それらを equivalent resistor。この等価抵抗器の抵抗は、これらすべての複数の抵抗器の抵抗の合計に等しくなります。

Note 1−インダクタンスがL ₁、L ₂、...、L _Nの「N」インダクタが直列に接続されている場合、equivalent inductance になります

$$L_{Eq} = L_1 + L_2 + ... + L_N$$

Note 2−静電容量がC ₁、C ₂、...、C _Nの「N」コンデンサが直列に接続されている場合、equivalent capacitance になります

$$\frac{1}{C_{Eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ... + \frac{1}{C_N}$$

並列等価回路

同様の受動素子が接続されている場合 parallelの場合、各要素で同じ電圧が維持されます。しかし、各要素を流れる電流は分割されます。

次のことを考慮してください circuit diagram。

これには、単一の電流源（I _S）と、抵抗がR ₁、R ₂、およびR3の₃つの抵抗があります。これらの要素はすべて並列に接続されています。電圧（V _S）は、これらすべての要素で利用できます。

上記の回路には、接地ノードを除いて1つの主ノード（P）しかありません。ザ・KCL equation このプリンシパルノード（P）では

$$I_S = I_1 + I_2 + I_3$$

代替 $I_1 = \frac{V_S}{R_1}, \: I_2 = \frac{V_S}{R_2}$ そして $I_3 = \frac{V_S}{R_3}$ 上記の式で。

$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} + \frac{V_S}{R_3}$$

$$\Rightarrow I_S = V_S \lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup$$

$$\Rightarrow V_S = I_S\left [ \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup} \right ]$$

上記の式は、V _S = I _S R _Eqの形式です。ここで、

$$R_{Eq} = \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup}$$

$$\frac{1}{R_{Eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$

ザ・ equivalent circuit diagram 与えられた回路のは次の図に示されています。

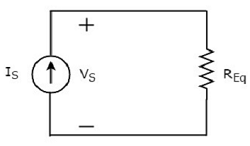
つまり、複数の抵抗が並列に接続されている場合は、それらを同等の抵抗に置き換えることができます。これの抵抗equivalent resistor これらすべての複数の抵抗器の各抵抗の逆数の合計の逆数に等しくなります。

Note 1−インダクタンスがL ₁、L ₂、...、L _Nの「N」インダクタが並列に接続されている場合、equivalent inductance になります

$$\frac{1}{L_{Eq}} = \frac{1}{L_1} + \frac{1}{L_2} + ... + \frac{1}{L_N}$$

Note 2−静電容量がC ₁、C ₂、...、C _Nの「N」コンデンサが並列に接続されている場合、equivalent capacitance になります

$$C_{Eq} = C_1 + C_2 + ... + C_N$$

前章では、直列結合と並列結合の等価回路について個別に説明しました。この章では、同様の受動素子の直列と並列の両方の組み合わせを検討することにより、問題の例を解決しましょう。

例

見つけましょう equivalent resistance 次の電気ネットワークの端子AとBの間。

上記のネットワークをこれら2つの端子間の単一の抵抗に最小化することにより、端子AとB間の等価抵抗を取得します。このために、私たちはしなければなりませんidentify the combination of resistors 直列形式と並列形式で接続され、すべてのステップでそれぞれの形式の等価抵抗を見つけます。

与えられた電気ネットワークは modified 次の図に示すように、次の形式に変換します。

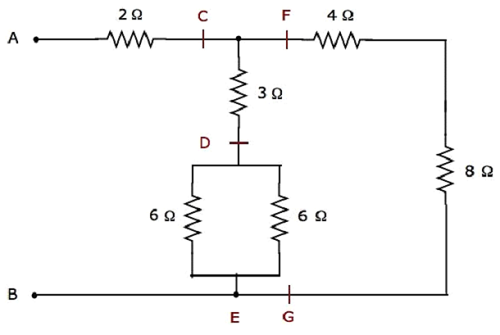
上の図では、CからGの文字は、さまざまな端子のラベル付けに使用されています。

Step 1 −上記のネットワークでは、2つ 6 Ω resistors で接続されています parallel。したがって、DとEの間の等価抵抗は3Ωになります。これは、次の簡略化を行うことで取得できます。

$$R_{DE} = \frac{6 \times 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$

上記のネットワークでは、抵抗器 4 Ω そして 8 Ω で接続されています series。したがって、FとGの間の等価抵抗は12Ωになります。これは、次の簡略化を行うことで取得できます。

$$R_{FG} = 4 + 8 = 12 \Omega$$

Step 2 −簡略化された電気 network after Step 1 次の図に示します。

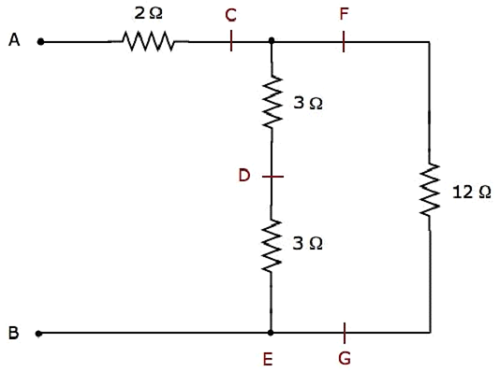
上記のネットワークでは、2つ 3 Ω resistors で接続されています series。したがって、CとEの間の等価抵抗は次のようになります。6 Ω。これは、次の簡略化を行うことで取得できます。

$$R_{CE} = 3 + 3 = 6 \Omega$$

Step 3 −簡略化された電気 network after Step 2 次の図に示します。

上記のネットワークでは、抵抗器 6 Ω そして 12 Ω で接続されています parallel。したがって、CとBの間の等価抵抗は4Ωになります。これは、次の簡略化を行うことで取得できます。

$$R_{CB} = \frac{6 \times 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$

Step 4 −簡略化された電気 network after Step 3 次の図に示します。

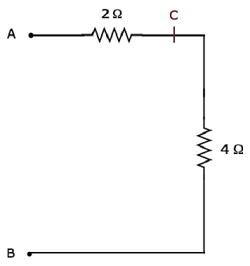
上記のネットワークでは、抵抗器 2 Ω そして 4 Ω で接続されています seriesしたがって、AとBの間の等価抵抗は6Ωになります。これは、次の簡略化を行うことで取得できます。

$$R_{AB} = 2 + 4 = 6 \Omega$$

したがって、特定の電気ネットワークの端子AとBの間の等価抵抗は次のようになります。 6 Ω。

前の章では、等価抵抗に関連する問題の例について説明しました。そこで、計算しましたequivalent resistance与えられた電気ネットワークの端子AとBの間で簡単に。なぜなら、すべてのステップで、直列形式または並列形式のいずれかで接続された抵抗の組み合わせを取得したからです。

ただし、状況によっては、以前のアプローチに従ってネットワークを単純化することが難しい場合があります。たとえば、デルタ（δ）形式またはスター形式のいずれかで接続された抵抗。そのような状況では、私たちはしなければなりませんconvert直列の組み合わせまたは並列の組み合わせを使用してさらに単純化するために、ある形式から別の形式のネットワーク。この章では、Delta to Star Conversion。

デルタネットワーク

次のことを考慮してください delta network 次の図に示すように。

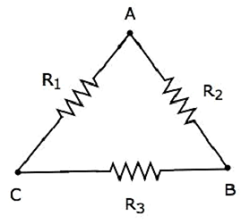
次の方程式は、 equivalent resistance デルタネットワークの2つの端末間で、3番目の端末が開いたままの場合。

$$R_{AB} = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$$

$$R_{BC} = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$$

$$R_{CA} = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$$

スターネットワーク

次の図は、 equivalent star network 上記のデルタネットワークに対応します。

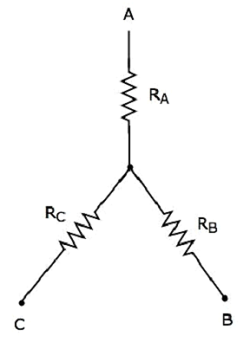
次の方程式は、 equivalent resistance スターネットワークの2つの端末間で、3番目の端末が開いたままの場合。

$$R_{AB} = R_A + R_B$$

$$R_{BC} = R_B + R_C$$

$$R_{CA} = R_C + R_A$$

デルタネットワーク抵抗の観点からのスターネットワーク抵抗

左側の項が同じである上記の方程式の右側の項を等しくすることにより、次の方程式が得られます。

$R_A + R_B = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$ Equation 1

$R_B + R_C = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$ Equation 2

$R_C + R_A = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$ Equation 3

上記の3つの方程式を追加すると、次のようになります。

$$2(R_A + R_B + R_C) = \frac{2(R_1 R_2 + R_2 R_3 + R_3 R_1)}{R_1 + R_2 + R_3}$$

$\Rightarrow R_A + R_B + R_C = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3}$ Equation 4

式4から式2を引きます。

$R_A + R_B + R_C - (R_B + R_C) = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3} - \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$

$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$

式4から式3を引くと、次のようになります。

$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$

式4から式1を引くと、次のようになります。

$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$

上記の関係を使用することにより、デルタネットワークの抵抗からスターネットワークの抵抗を見つけることができます。このようにして、delta network に star network。

例

計算してみましょう resistances of star network、次の図に示すように、デルタネットワークと同等です。

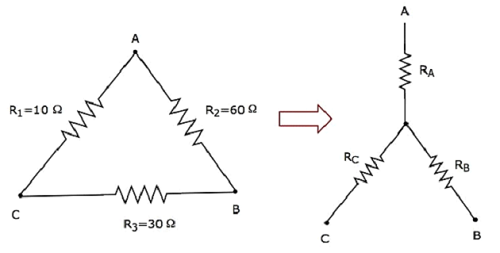
与えられた resistances of delta networkR ₁ = 10Ω、R ₂ = 60ΩかつR ₃ = 30Ω。

デルタネットワークの抵抗の観点から、スターネットワークの抵抗の次の関係を知っています。

$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$

$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$

$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$

値を代入R ₁、R ₂及びR _3は上記式に。

$$R_A = \frac{10 \times 60}{10 +60+30} = \frac{600}{100} = 6\Omega$$

$$R_B = \frac{60 \times 30}{10 +60+30} = \frac{1800}{100} = 18\Omega$$

$$R_C = \frac{30 \times 10}{10 +60+30} = \frac{300}{100} = 3\Omega$$

だから、私たちはスターネットワークの抵抗を得ました R_A = 6 Ω, R_B = 18 Ω そして R_C = 3 Ω、これは、特定のデルタネットワークの抵抗に相当します。

前の章では、デルタネットワークの同等のスターネットワークへの変換について説明しました。それでは、スターネットワークから同等のデルタネットワークへの変換について説明しましょう。この変換は、Star to Delta Conversion。

前の章では、 resistances of star network デルタネットワークから

$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ Equation 1

$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ Equation 2

$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ Equation 3

スターネットワーク抵抗の観点からのデルタネットワーク抵抗

スターネットワークの抵抗の観点からデルタネットワークの抵抗を取得するために、上記の方程式を操作してみましょう。

• Multiply 2つの方程式の各セットそして add。

$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$

$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$

$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ Equation 4

• 式4を式2で割ると、次のようになります。

$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$

$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

• 式4を式3で割ると、次のようになります。

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

• 式4を式1で割ると、次のようになります。

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

上記の関係を使用することにより、スターネットワークの抵抗からデルタネットワークの抵抗を見つけることができます。このようにして、変換することができますstar network into delta network。

例

計算してみましょう resistances of delta network、次の図に示すように、スターネットワークと同等です。

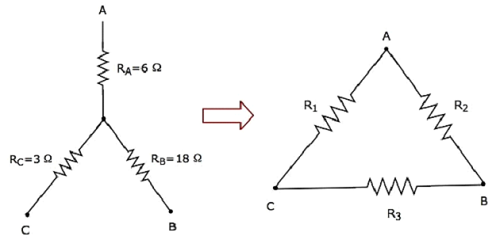
与えられた resistances of star networkR _A = 6Ω、R _B = 18Ω及びR _C = 3Ω。

私たちは次の関係を知っています resistances of delta network スターネットワークの抵抗の観点から。

$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

値を代入R _A、R _BおよびR _Cが上記の式に。

$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$

$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$

$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$

したがって、デルタネットワークの抵抗は次のようになります。 R₁ = 10 Ω, R₂ = 60 Ω そして R₃ = 30 Ω、これは特定のスターネットワークの抵抗に相当します。

ネットワークトポロジは、電気回路をグラフィカルに表現したものです。複雑な電気回路をネットワークグラフに変換して分析するのに便利です。ネットワークトポロジは、Graph theory。

ネットワークトポロジの基本的な用語

ここで、このネットワークトポロジに関連する基本的な用語について説明します。

グラフ

ネットワークグラフは単に次のように呼ばれます graph。これは、ブランチで接続されたノードのセットで構成されています。グラフでは、ノードは2つ以上のブランチの共通点です。場合によっては、単一のブランチのみがノードに接続することがあります。分岐は、2つのノードを接続する線分です。

任意の電気回路またはネットワークを同等のものに変換できます graph受動素子と電圧源を短絡に、電流源を開回路に置き換えることによって。つまり、グラフの線分は、受動素子または電気回路の電圧源のいずれかに対応する分岐を表しています。

例

次のことを考えてみましょう electric circuit。

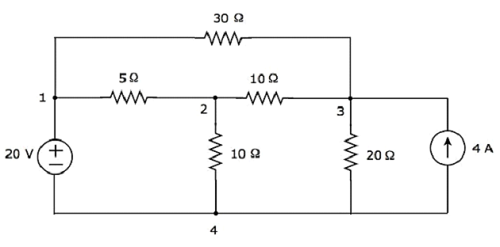
上記の回路には、 four principal nodes そしてそれらは1、2、3、および4でラベル付けされています。 seven branches 上記の回路では、1つのブランチに20 Vの電圧源が含まれ、別のブランチに4 Aの電流源が含まれ、残りの5つのブランチにはそれぞれ30Ω、5Ω、10Ω、10Ω、20Ωの抵抗が含まれています。

同等のもの graph 上記の電気回路に対応するものを下図に示します。

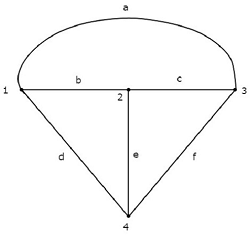
上のグラフには、 four nodesそしてそれらはそれぞれ1、2、3、4のラベルが付いています。これらは、電気回路の主要ノードのそれと同じです。があるsix branches 上のグラフでは、それらにはそれぞれa、b、c、d、e、fのラベルが付いています。

この場合、 one branch less 電気回路を同等のグラフに変換しながら、4Aの電流源を開回路として作成しているためです。

この例から、次の点を結論付けることができます-

• ザ・ number of nodes グラフに存在するのは、電気回路に存在する主要ノードの数に等しくなります。

• ザ・ number of branches グラフに存在するものは、電気回路に存在する分岐の数以下になります。

グラフの種類

グラフの種類は次のとおりです-

• コネクテッドグラフ
• 接続されていないグラフ
• 有向グラフ
• 無向グラフ

それでは、これらのグラフを1つずつ説明していきましょう。

コネクテッドグラフ

グラフの2つのノードのいずれかに少なくとも1つの分岐が存在する場合、それは connected graph。つまり、接続されたグラフの各ノードには、それに接続された1つ以上のブランチがあります。したがって、ノードが分離または分離された状態で表示されることはありません。

前の例に示されているグラフは connected graph。ここでは、すべてのノードが3つのブランチで接続されています。

接続されていないグラフ

グラフ内に単一のブランチでも接続されていないノードが少なくとも1つ存在する場合、それは unconnected graph。したがって、接続されていないグラフには1つ以上の孤立したノードがあります。

次の図に示すグラフについて考えてみます。

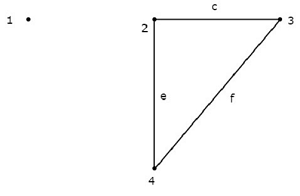
このグラフでは、ノード2、3、および4はそれぞれ2つのブランチで接続されています。しかし、1つのブランチでさえ接続されていませんnode 1。したがって、ノード1はisolated node。したがって、上のグラフはunconnected graph。

有向グラフ

グラフのすべてのブランチが矢印で表されている場合、そのグラフは directed graph。これらの矢印は、各ブランチの電流の方向を示しています。したがって、このグラフは次のようにも呼ばれます。oriented graph。

次の図に示すグラフについて考えてみます。

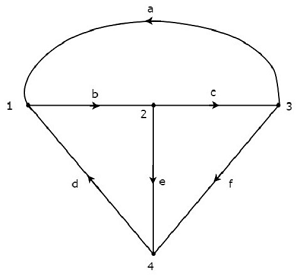
上のグラフでは、電流の流れの方向が各ブランチに矢印で表されています。したがって、それはdirected graph。

無向グラフ

グラフの分岐が矢印で表されていない場合、そのグラフは undirected graph。電流の方向がないため、このグラフはunoriented graph。

この章の最初の例で示したグラフは、 unoriented graph、そのグラフのブランチに矢印がないためです。

サブグラフとそのタイプ

グラフの一部は、 subgraph。特定のグラフのいくつかのノードやブランチを削除することでサブグラフを取得します。したがって、サブグラフのブランチやノードの数は、元のグラフの数よりも少なくなります。したがって、サブグラフはグラフのサブセットであると結論付けることができます。

以下は two types サブグラフの。

• Tree
• Co-Tree

木

ツリーは、特定のグラフの接続されたサブグラフであり、グラフのすべてのノードが含まれています。ただし、そのサブグラフにはループがあってはなりません。木の枝は次のように呼ばれますtwigs。

次のことを考慮してください connected subgraph この章の冒頭の例に示されているグラフの。

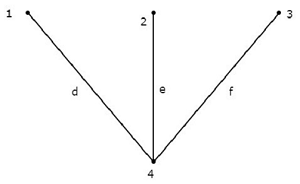
この接続されたサブグラフには、指定されたグラフの4つのノードすべてが含まれ、ループはありません。したがって、それはTree。

このツリーには、指定されたグラフの6つのブランチのうち3つのブランチしかありません。なぜなら、グラフの残りのブランチの1つのブランチでさえ考慮すると、上記の接続されたサブグラフにループが存在するからです。その場合、結果の接続されたサブグラフはツリーではなくなります。

上記のツリーから、次のように結論付けることができます。 number of branches ツリーに存在するものは、 n - 1 ここで、「n」は指定されたグラフのノードの数です。

コツリー

Co-Treeはサブグラフであり、ツリーの形成中に削除されたブランチで形成されます。したがって、それはとして呼ばれますComplement木の。すべてのツリーに対して、対応するCo-Treeがあり、そのブランチは次のように呼ばれます。linksまたは和音。通常、リンクは点線で表されます。

ザ・ Co-Tree 上記のツリーに対応するものを次の図に示します。

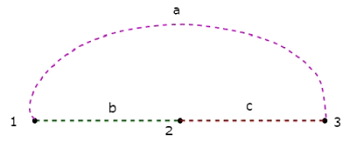
ノード4は上記のCo-Treeから分離されているため、このCo-Treeには、指定されたグラフの4つのノードではなく3つのノードしかありません。したがって、Co-Treeは接続されたサブグラフである必要はありません。このCo-Treeには3つのブランチがあり、それらはループを形成します。

ザ・ number of branchesコツリーに存在するものは、特定のグラフの枝の数と小枝の数の差に等しくなります。数学的には、次のように書くことができます

$$l = b - (n - 1)$$

$$l = b - n + 1$$

どこ、

• l リンクの数です。
• b は、特定のグラフに存在するブランチの数です。
• n 特定のグラフに存在するノードの数です。

ツリーとそれに対応するCo-Treeを組み合わせると、次のようになります。 original graph 以下に示すように。

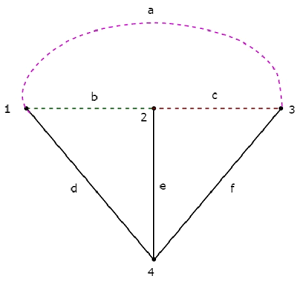
木の枝d、e、fは実線で表されます。Co-Treeブランチa、b、cは破線で表されます。

前の章では、電気回路を同等のグラフに変換する方法について説明しました。次に、同等のグラフを使用して、電気回路またはネットワークの問題を解決するのに役立つネットワークトポロジ行列について説明します。

ネットワークグラフに関連付けられた行列

以下は、グラフ理論で使用される3つの行列です。

• 接続行列
• 基本的なループマトリックス
• ファンダメンタルカットセットマトリックス

接続行列

接続行列は、特定の電気回路またはネットワークのグラフを表します。したがって、同じ電気回路またはネットワークのグラフをから描くことができます。incidence matrix。

グラフはノードのセットで構成されており、それらはいくつかのブランチで接続されていることがわかっています。したがって、ブランチをノードに接続することを発生率と呼びます。接続行列は文字Aで表されます。これは、ノードから分岐への接続行列またはnode incidence matrix。

'n'ノードがあり、 'b'ブランチがaに存在する場合 directed graphの場合、接続行列には「n」行と「b」列があります。ここで、行と列は有向グラフのノードとブランチに対応しています。従ってorder 接続行列の n × b。

ザ・ elements of incidence matrix + 1、-1、0の3つの値のいずれかになります。

• 分岐電流が選択したノードから出ている場合、要素の値は+1になります。

• 分岐電流が選択したノードに向かって入っている場合、要素の値は-1になります。

• 分岐電流が選択されたノードに流入せず、選択されたノードから流出しない場合、要素の値は0になります。

接続行列を見つける手順

有向グラフの接続行列を見つけるには、次の手順に従います。

• 指定された有向グラフの時点でノードを選択し、そのノードに対応する接続​​行列の要素の値を行に入力します。

• 指定された有向グラフのすべてのノードに対して上記の手順を繰り返します。

例

次のことを考慮してください directed graph。

ザ・ incidence matrix 上記の有向グラフに対応します

$$A = \begin{bmatrix}-1 & 1 & 0 & -1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \\0 & 0 & 0 & 1 & -1 & -1 \end{bmatrix}$$

上記の行列の行と列は、指定された有向グラフのノードとブランチを表します。この接続行列の次数は4×6です。

上記の接続行列を観察することにより、次のように結論付けることができます。 summation接続行列の列要素の数はゼロに等しい。つまり、分岐電流は1つのノードから出て、別の単一ノードにのみ入ります。

Note−与えられたグラフが無向タイプの場合、その各ブランチの矢印を表すことにより、それを有向グラフに変換します。各分岐に流れる電流の任意の方向を考慮することができます。

基本的なループマトリックス

基本的なループまたは f-loopはループであり、1つのリンクと1つ以上の小枝のみが含まれています。したがって、fループの数はリンクの数と等しくなります。基本的なループ行列は文字Bで表されます。これは次のようにも呼ばれます。fundamental circuit matrixおよびタイセット行列。この行列は、分岐電流とリンク電流の関係を示します。

'n'ノードがあり、 'b'ブランチがaに存在する場合 directed graphの場合、指定されたグラフの選択されたツリーに対応する、コツリーに存在するリンクの数はb-n +1になります。

したがって、基本的なループ行列には「b-n +1」行と「b」列があります。ここで、行と列は、指定されたグラフのコツリーとブランチのリンクに対応しています。したがって、基本ループ行列の次数は次のようになります。(b - n + 1) × b。

ザ・ elements of fundamental loop matrix + 1、-1、0の3つの値のいずれかになります。

• 選択したfループのリンクの要素の値は+1になります。

• 選択したfループの一部ではない残りのリンクと小枝の要素の値は0になります。

• 選択したfループの小枝電流の方向がfループリンク電流の方向と同じである場合、要素の値は+1になります。

• 選択したfループの小枝電流の方向がfループリンク電流の方向と反対の場合、要素の値は-1になります。

基本的なループ行列を見つける手順

与えられた有向グラフの基本的なループ行列を見つけるために、これらのステップに従ってください。

• 与えられた有向グラフのツリーを選択します。

• 一度に1つのリンクを含めることにより、1つのfループを取得します。このfループに対応する要素の値を基本ループ行列の行に入力します。

• すべてのリンクに対して上記の手順を繰り返します。

例

次のツリーを見てください directed graph、これは接続行列と見なされます。

上記のツリーには、3つのブランチd、e、fが含まれています。したがって、ブランチa、b、cは、上記のツリーに対応するCo-Treeのリンクになります。上記のツリーへのリンクを一度に1つ含めると、1つになります。f-loop。だから、3つありますf-loops、3つのリンクがあるため。これらの3つのfループを次の図に示します。

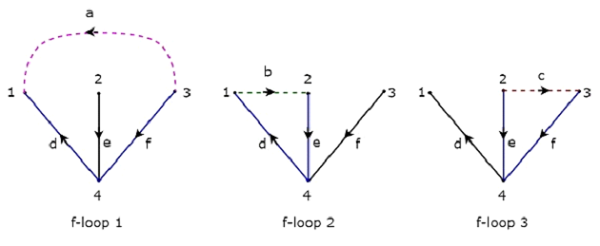
上の図では、色付きの線で表されているブランチがfループを形成しています。各fループからタイセット行列の行ごとの要素値を取得します。だから、Tieset matrix 上記の考慮されたツリーの

$$B = \begin{bmatrix}1 & 0 & 0 & -1 & 0 & -1\\0 & 1 & 0 & 1 & 1 & 0\\0 & 0 & 1 & 0 & -1 & 1 \end{bmatrix}$$

上記の行列の行と列は、指定された有向グラフのリンクとブランチを表しています。この接続行列の次数は3×6です。

ザ・ number of Fundamental loop matrices有向グラフの数は、その有向グラフのツリーの数に等しくなります。なぜなら、すべてのツリーには1つの基本ループ行列があるからです。

基本的なカットセットマトリックス

ファンダメンタルカットセットまたは f-cut setは、元のグラフが2つの分離されたサブグラフになるようにグラフから削除されるブランチの最小数です。Fカットセットにはone twigおよび1つ以上のリンク。したがって、fカットセットの数は小枝の数と同じになります。

Fundamental cut set matrix は文字Cで表されます。この行列は、分岐電圧と小枝電圧の関係を示します。

'n'ノードがあり、 'b'ブランチがaに存在する場合 directed graphの場合、指定されたグラフの選択されたツリーに存在する小枝の数はn-1になります。したがって、基本的なカットセット行列には「n-1」行と「b」列があります。ここで、行と列は、選択したツリーの小枝と特定のグラフの枝に対応しています。従ってorder 基本カットセットマトリックスの (n-1) × b。

ザ・ elements of fundamental cut set matrix + 1、-1、0の3つの値のいずれかになります。

• 要素の値は、選択したfカットセットの小枝に対して+1になります。

• 選択したfカットセットの一部ではない残りの小枝とリンクの要素の値は0になります。

• 選択したfカットセットのリンク電流の方向がfカットセットの小枝電流の方向と同じである場合、要素の値は+1になります。

• 選択したfカットセットのリンク電流の方向がfカットセットの小枝電流の方向と反対の場合、要素の値は-1になります。

基本的なカットセットマトリックスを見つける手順

与えられた有向グラフの基本的なカットセット行列を見つけるために、これらのステップに従ってください。

• 与えられた有向グラフのツリーを選択し、点線でリンクを表します。

• 一度に1本の小枝と必要なリンクを取り除くことで、1つのfカットセットを手に入れることができます。このfカットセットに対応する要素の値を基本カットセット行列の行に入力します。

• すべての小枝に対して上記の手順を繰り返します。

例

同じことを考えてください directed graph 、これは接続行列のセクションで説明しました。この有向グラフのブランチd、e、fを小枝として選択します。したがって、この有向グラフの残りのブランチa、b、cがリンクになります。

ザ・ twigs d、e、fは実線で表され、 links 次の図では、a、b、cが点線で表されています。

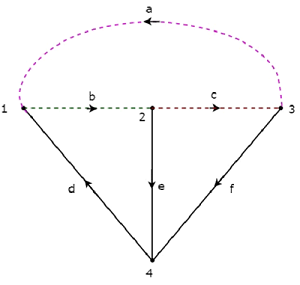
一度に1本の小枝と必要なリンクを取り除くことで、1つのfカットセットを手に入れることができます。つまり、小枝が3つあるので、fカットセットは3つになります。これらの3つf-cut sets 次の図に示します。

C ₁、C ₂、C ₃の小枝とリンクのセットを削除することにより、3つのfカットセットを作成します。各fカットセットから基本カットセット行列の行ごとの要素値を取得します。だから、fundamental cut set matrix 上記の考慮されたツリーの

$$C = \begin{bmatrix}1 & -1 & 0 & 1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \end{bmatrix}$$

上記の行列の行と列は、指定された有向グラフの小枝と枝を表しています。この基本的なカットセット行列の次数は3×6です。

ザ・ number of Fundamental cut set matrices有向グラフの数は、その有向グラフのツリーの数に等しくなります。なぜなら、すべてのツリーには1つの基本カットセットマトリックスがあるからです。

Superposition theorem電気回路の応答と励起の間の線形性の概念に基づいています。複数の独立したソースが同時に動作している場合の線形回路の特定の分岐での応答は、各独立したソースが同時に動作しているための応答の合計に等しいと述べています。

この方法では、のみを考慮します one independent source一度に。したがって、回路から残りの独立したソースを排除する必要があります。2つの端子を短絡することで電圧源を排除でき、同様に2つの端子を開くことで電流源を排除できます。

したがって、特定のブランチで応答を見つける必要があります ‘n’ times'n'の独立したソースがある場合。特定のブランチでの応答は、そのブランチを流れる電流またはそのブランチの両端の電圧のいずれかである可能性があります。

重ね合わせの原理の手順

重ね合わせの原理を使用して特定のブランチの応答を見つけるには、次の手順に従います。

Step 1 − 1つの独立したソースを検討し、ネットワークに存在する残りの独立したソースを排除することにより、特定のブランチでの応答を見つけます。

Step 2 −ネットワークに存在するすべての独立したソースに対して手順1を繰り返します。

Step 3 −すべての独立したソースがネットワークに存在する場合に特定のブランチで全体的な応答を取得するために、すべての応答を追加します。

例

次の回路の20Ω抵抗を流れる電流を superposition theorem。

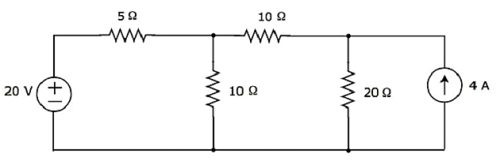
Step 1 −20Ω抵抗を流れる電流を考慮してみよう 20 V voltage source。この場合、4Aの電流源を開回路にすることで電流源をなくすことができます。変更した回路図を次の図に示します。

上記の回路では、グラウンドを除いて主要ノードは1つだけです。だから、私たちは使用することができますnodal analysis方法。ノード電圧V _1は、次の図に標識されます。ここで、V ₁は、ノード1からのグランドに対する電圧です。

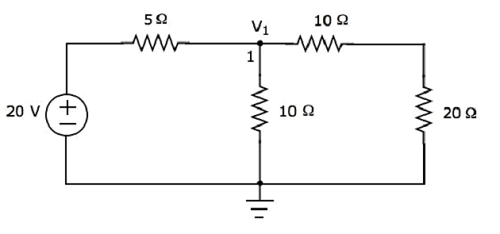
ザ・ nodal equation ノード1には

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1}{10 + 20} = 0$$

$$\Rightarrow \frac{6V_1 - 120 + 3V_1 + V_1}{30} = 0$$

$$\Rightarrow 10V_1 = 120$$

$$\Rightarrow V_1 = 12V$$

ザ・ current flowing through 20 Ω resistor 次の簡略化を行うことで見つけることができます。

$$I_1 = \frac{V_1}{10 + 20}$$

Vの値が代入_1を上式に。

$$I_1 = \frac{12}{10 + 20} = \frac{12}{30} = 0.4 A$$

したがって、20Ωの抵抗を流れる電流は 0.4 A、20Vの電圧源のみを考慮した場合。

Step 2 −20Ω抵抗を流れる電流を考慮してみよう 4 A current source。この場合、20Vの電圧源を短絡させることで電圧源をなくすことができます。変更した回路図を次の図に示します。

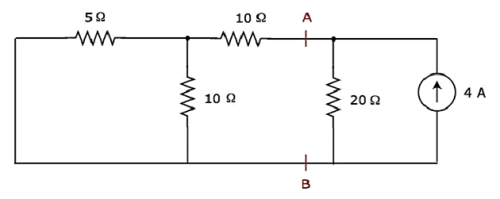
上記の回路では、端子AとBの左側に3つの抵抗があります。これらの抵抗を1つの抵抗に置き換えることができます。 equivalent resistor。ここでは、5Ωと10Ωの抵抗が並列に接続されており、組み合わせ全体が10Ωの抵抗と直列になっています。

ザ・ equivalent resistance 端子AとBの左側は

$$R_{AB} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$

簡略化した回路図を次の図に示します。

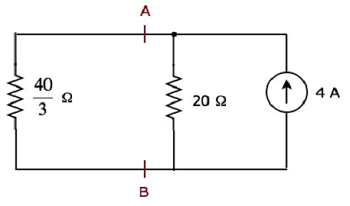
を使用して、20Ωの抵抗を流れる電流を見つけることができます current division principle。

$$I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$

代替 $I_S = 4A,\: R_1 = \frac{40}{3} \Omega$ そして $R_2 = 20 \Omega$ 上記の式で。

$$I_2 = 4 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup = 4 \lgroup \frac{40}{100} \rgroup = 1.6 A$$

したがって、20Ωの抵抗を流れる電流は 1.6 A、4Aの電流源のみを考慮した場合。

Step 3 −与えられた回路の20Ω抵抗を流れる電流を得るには、 addition of two currents ステップ1とステップ2で得たものです。数学的には、次のように書くことができます。

$$I = I_1 + I_2$$

代替の値I ₁及びI ₂上記の式です。

$$I = 0.4 + 1.6 = 2 A$$

したがって、特定の回路の20Ω抵抗を流れる電流は次のようになります。 2 A。

Note −の量を求めるために、重ね合わせの原理を直接適用することはできません。 power線形回路に存在する抵抗器に供給されるのは、それぞれの独立したソースによってその抵抗器に供給される電力を加算するだけです。むしろ、重ね合わせの原理を使用して、その抵抗器を流れる総電流またはその抵抗器の両端の電圧を計算でき、そこから、$I^2 R$ または $\frac{V^2}{R}$。

Thevenin’s theoremは、任意の2端子線形ネットワークまたは回路を、抵抗と直列の電圧源で構成される同等のネットワークまたは回路で表すことができると述べています。テブナンの等価回路として知られています。線形回路には、独立したソース、依存したソース、および抵抗が含まれる場合があります。

回路に複数の独立したソース、依存したソース、および抵抗が含まれている場合、要素の左側にあるネットワーク全体を次のように置き換えることで、要素の応答を簡単に見つけることができます。 Thevenin’s equivalent circuit。

ザ・ response in an element その要素の両端の電圧、その要素を流れる電流、またはその要素の両端で消費される電力のいずれかです。

この概念を次の図に示します。

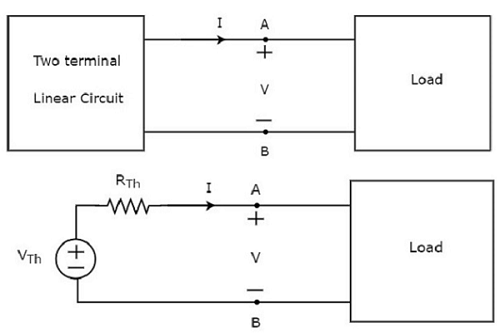
Thevenin’s equivalent circuit実用的な電圧源に似ています。したがって、抵抗と直列に電圧源があります。

• テブナンの等価回路に存在する電圧源は、テブナンの等価電圧または単に呼ばれます。 Thevenin’s voltage, V_Th。

• テブナンの等価回路に存在する抵抗は、テブナンの等価抵抗または単に呼ばれます。 Thevenin’s resistor, R_Th。

テブナンの等価回路を見つける方法

テブナンの等価回路を見つけるには3つの方法があります。に基づくtype of sourcesネットワークに存在する場合、これら3つの方法のいずれかを選択できます。それでは、2つの方法を1つずつ説明しましょう。次の章では、3番目の方法について説明します。

方法1

テブナンの等価回路を見つけるには、次の手順に従ってください。 sources of independent type 存在しています。

• Step 1 −テブナンの等価回路を見つけるための端子を開いて回路図を検討します。

• Step 2 −テブナンの電圧を見つける V_Th 上記の回路の開いた端子間。

• Step 3 −テブナンの抵抗を見つける R_Th その中に存在する独立したソースを排除することにより、上記の回路のオープン端子間で。

• Step 4 −を描く Thevenin’s equivalent circuitテブナンの電圧Vの接続によって_のThをテブナンの抵抗Rと直列_のTh。

これで、テブナンの等価回路の右側にある要素で応答を見つけることができます。

例

最初にaを見つけて、20Ωの抵抗を流れる電流を見つけます。 Thevenin’s equivalent circuit 端子AとBの左側。

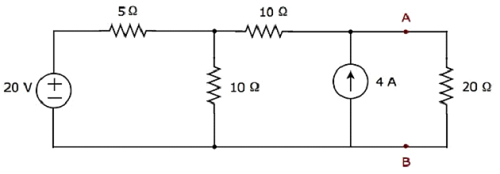
Step 1 −端子AとBの左側にあるテブナンの等価回路を見つけるには、次の方法でネットワークから20Ωの抵抗を削除する必要があります。 opening the terminals A & B。変更した回路図を次の図に示します。

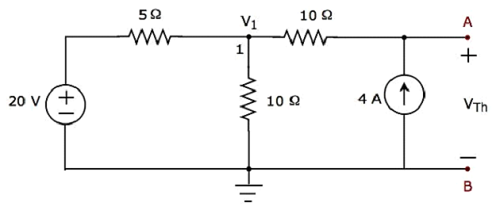
Step 2 −の計算 Thevenin’s voltage V_Th。

上記の回路では、グラウンドを除いて主要ノードは1つだけです。だから、私たちは使用することができますnodal analysis方法。ノード電圧V ₁とテブナンの電圧V _Thが上記の図に標識されます。ここで、V ₁はグランドに対するノード1からの電圧であり、_VThは4A電流源の両端の電圧です。

• ザ・ nodal equation ノード1には

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} - 4 = 0$$

$$\Rightarrow \frac{2V_1 - 40 + V_1 - 40}{10} = 0$$

$$\Rightarrow 3V_1 - 80 = 0$$

$$\Rightarrow V_1 = \frac{80}{3}V$$

• 直列分岐10Ω抵抗の両端の電圧は

$$V_{10 \Omega} = (-4)(10) = -40V$$

• 上記の回路には2つのメッシュがあります。ザ・KVL equation 2番目のメッシュの周りは

$$V_1 - V_{10 \Omega} - V_{Th} = 0$$

• の値を代入します $V_1$ そして $V_{10 \Omega}$ 上記の式で。

$$\frac{80}{3} - (-40) - V_{Th} = 0$$

$$V_{Th} = \frac{80 + 120}{3} = \frac{200}{3}V$$

• したがって、テブナンの電圧は $V_{Th} = \frac{200}{3}V$

Step 3 −の計算 Thevenin’s resistance R_Th。

短絡電圧源と開回路テブナンの抵抗値Rを計算するために、上記の回路の電流源_のThを端子A＆B.ザを横切ってmodified circuit diagram 次の図に示します。

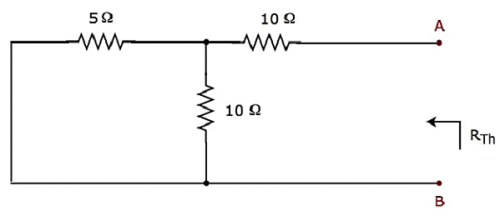
端子AとB間のテブナンの抵抗は

$$R_{Th} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$

したがって、テブナンの抵抗は $\mathbf {R_{Th} = \frac{40}{3} \Omega}$。

Step 4−テブナンの等価回路は、指定された回路の端子AとBの左側に配置されます。この回路図を次の図に示します。

20Ωの抵抗を流れる電流は、の値を代入することによって求めることができるV _Thを、R_のTh及びRを次式で。

$$l = \frac{V_{Th}}{R_{Th} + R}$$

$$l = \frac{\frac{200}{3}}{\frac{40}{3} + 20} = \frac{200}{100} = 2A$$

したがって、20Ωの抵抗を流れる電流は 2 A。

方法2

テブナンの等価回路を見つけるには、次の手順に従ってください。 sources of both independent type and dependent type 存在しています。

• Step 1 −テブナンの等価回路が見つかる端子を開いて、回路図を検討します。

• Step 2 −テブナンの電圧を見つける V_Th 上記の回路の開いた端子間。

• Step 3 −短絡電流を見つける I_SC 上記の回路の2つの開いた端子を短絡することによって。

• Step 4 −テブナンの抵抗を見つける R_Th 次の式を使用します。

$$R_{Th} = \frac{V_{Th}}{I_{SC}}$$

Step 5 −を描く Thevenin’s equivalent circuitテブナンの電圧Vの接続によって_のThをテブナンの抵抗Rと直列_のTh。

これで、テブナンの等価回路の右側にある要素で応答を見つけることができます。

Norton’s theoremテブナンの定理に似ています。これは、任意の2端子線形ネットワークまたは回路を、抵抗と並列の電流源で構成される同等のネットワークまたは回路で表すことができると述べています。それはとして知られていますNorton’s equivalent circuit。線形回路には、独立したソース、依存したソース、および抵抗が含まれる場合があります。

回路に複数の独立したソース、依存したソース、および抵抗がある場合、要素の左側にあるネットワーク全体を次のように置き換えることで、要素の応答を簡単に見つけることができます。 Norton’s equivalent circuit。

ザ・ response in an element その要素の両端の電圧、その要素を流れる電流、またはその要素の両端で消費される電力のいずれかです。

この概念を次の図に示します。

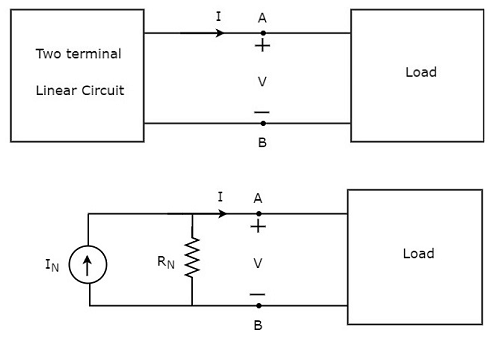
Norton’s equivalent circuit実用的な電流源に似ています。したがって、抵抗と並列に電流源があります。

• ノートンの等価回路に存在する電流源は、ノートンの等価電流または単に呼ばれます。 Norton’s current I_N。

• ノートンの等価回路に存在する抵抗は、ノートンの等価抵抗または単に呼ばれます。 Norton’s resistor R_N。

ノートンの等価回路を見つける方法

がある three methodsノートンの等価回路を見つけるため。ネットワークに存在するソースのタイプに基づいて、これら3つの方法のいずれかを選択できます。それでは、これら3つの方法を1つずつ説明していきましょう。

方法1

ノートンの等価回路を見つけるには、次の手順に従ってください。 sources of independent type 存在しています。

• Step 1 −ノートンの等価回路が見つかる端子を開いて回路図を検討します。

• Step 2 −ノートンの現在の電流を見つける I_N 上記の回路の2つの開いた端子を短絡することによって。

• Step 3 −ノートンの抵抗を見つける R_Nステップ1で検討した回路のオープン端子間で、そこに存在する独立したソースを排除します。ノートンの抵抗R_N テブナンの抵抗と同じになります R_Th。

• Step 4 −を描く Norton’s equivalent circuitノートンの抵抗Rと並列にノートンの電流INを接続することにより_N。

これで、ノートンの等価回路の右側にある要素で応答を見つけることができます。

方法2

ノートンの等価回路を見つけるには、次の手順に従ってください。 sources of both independent type and dependent type 存在しています。

• Step 1 −ノートンの等価回路を見つけるための端子を開いて回路図を検討します。

• Step 2 −開回路電圧を見つける V_OC 上記の回路の開いた端子間。

• Step 3 −ノートンの現在の電流を見つける I_N 上記の回路の2つの開いた端子を短絡することによって。

• Step 4 −ノートンの抵抗を見つける R_N 次の式を使用します。

$$R_N = \frac{V_{OC}}{I_N}$$

• Step 5-ノートンの電流I接続することにより、ノートンの等価回路を描画_Nをノートンの抵抗Rと並列に_N。

これで、ノートンの等価回路の右側にある要素で応答を見つけることができます。

方法3

これは、ノートンの等価回路を見つけるための代替方法です。

• Step 1 −検索 Thevenin’s equivalent circuit目的の2つの端子間。私たちは、それはテブナンの電圧源、Vで構成されていることを知っている_のThとテブナンの抵抗、R_のTh。

• Step 2 −適用 source transformation technique上記のテブナンの等価回路に。ノートンの等価回路を取得します。ここに、

ノートンの現在、

$$I_N = \frac{V_{Th}}{R_{Th}}$$

ノートンの抵抗、

$$R_N = R_{Th}$$

この概念を次の図に示します。

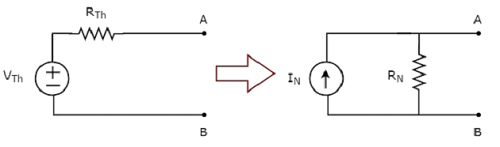
これで、ノートンの等価回路をその要素の左側に配置することにより、要素内の応答を見つけることができます。

Note−同様に、最初にノートンの等価回路を見つけてから、ソース変換手法を適用することで、テブナンの等価回路を見つけることができます。この概念を次の図に示します。

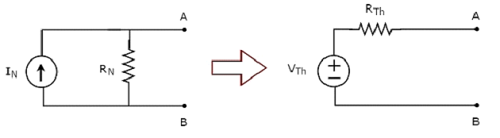
これは、テブナンの等価回路を見つけるための方法3です。

例

最初にaを見つけて、20Ωの抵抗を流れる電流を見つけます。 Norton’s equivalent circuit 端子AとBの左側。

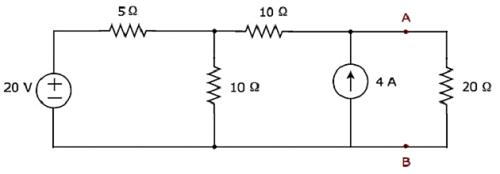
を使用してこの問題を解決しましょう Method 3。

Step 1−前章では、端子AとBの左側にあるテブナンの等価回路を計算しました。これでこの回路を使用できます。次の図に示します。

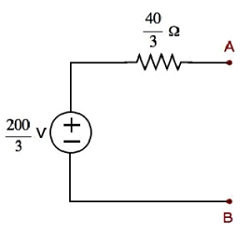
ここで、テブナンの電圧、 $V_{Th} = \frac{200}{3} V$ テブナンの抵抗、 $R_{Th} = \frac{40}{3} \Omega$

Step 2 −適用 source transformation technique上記のテブナンの等価回路に。値を代入しV_のTh及びR_のThを以下の式にNorton’s current。

$$I_N = \frac{V_{Th}}{R_{Th}}$$

$$I_N = \frac{\frac{200}{3}}{\frac{40}{3}} = 5A$$

したがって、ノートンの現在のI _Nがあります5 A。

私たちは、ノートンの抵抗、ということを知っているR _Nは、テブナンの抵抗の場合と同様であるR_のTh。

$$\mathbf {R_N = \frac{40}{3} \Omega}$$

上記のテブナンの等価回路に対応するノートンの等価回路を次の図に示します。

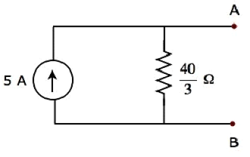
ここで、ノートンの等価回路を、指定された回路の端子AとBの左側に配置します。

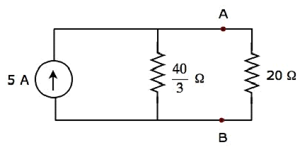
を使用して current division principle、20Ω抵抗を流れる電流は

$$I_{20 \Omega} = 5 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup$$

$$I_{20 \Omega} = 5 \lgroup \frac{40}{100} \rgroup = 2A$$

したがって、20Ωの抵抗を流れる電流は 2 A。

負荷が受け取る電力量は、電気および電子アプリケーションの重要なパラメータです。直流回路では、我々は、Rの抵抗値を有する抵抗で負荷を表すことができる_Lのオーム。同様に、交流回路において、我々は、Zのインピーダンスを有する複合負荷でそれを表すことができる_Lのオーム。

Maximum power transfer theorem DC電圧源は、負荷抵抗がソース抵抗と等しい場合にのみ、可変負荷抵抗に最大電力を供給すると述べています。

同様に、 Maximum power transfer theorem AC電圧源は、負荷インピーダンスがソースインピーダンスの複素共役に等しい場合にのみ、可変複素負荷に最大電力を供給すると述べています。

この章では、DC回路の最大電力伝達定理について説明します。

最大電力伝達定理の証明

Rの抵抗値を有する可変負荷抵抗の左側に任意の二つの末端線ネットワークまたは回路交換_Lのテブナンの等価回路とのオーム。テブナンの等価回路は実際の電圧源に似ていることがわかっています。

この概念を次の図に示します。

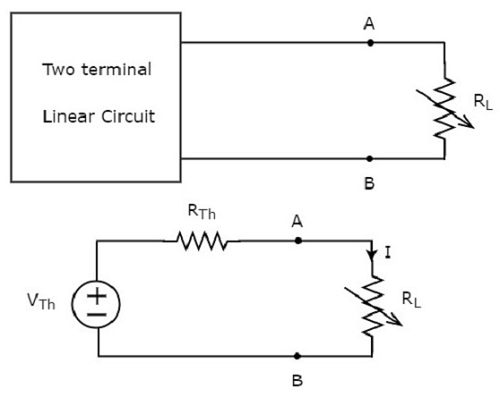
負荷抵抗の両端で消費される電力量は次のとおりです。

$$P_L = I^2 R_L$$

代替 $I = \frac{V_{Th}}{R_{Th} + R_L}$ 上記の式で。

$$P_L = \lgroup \frac{V_{Th}}{(R_{Th} + R_L)} \rgroup ^2 R_L$$

$\Rightarrow P_L = {V_{Th}}^2 \lbrace \frac{R_L}{(R_{Th} + R_L)^2} \rbrace$ Equation 1

最大電力伝達の条件

最大または最小の場合、一次導関数はゼロになります。したがって、式1をR _Lに関して微分し、ゼロに等しくします。

$$\frac{dP_L}{dR_L} = {V_{Th}}^2 \lbrace \frac{(R_{Th} + R_L)^2 \times 1 - R_L \times 2(R_{Th} + R_L)}{(R_{Th} + R_L)^4} \rbrace = 0$$

$$\Rightarrow (R_{Th} + R_L)^2 -2R_L(R_{Th} + R_L) = 0$$

$$\Rightarrow (R_{Th} + R_L)(R_{Th} + R_L - 2R_L) = 0$$

$$\Rightarrow (R_{Th} - R_L) = 0$$

$$\Rightarrow R_{Th} = R_L\:or\:R_L = R_{Th}$$

したがって、 condition for maximum power 負荷全体の消費は $R_L = R_{Th}$。つまり、負荷抵抗の値がソース抵抗の値、つまりテブナンの抵抗と等しい場合、負荷全体で消費される電力は最大値になります。

最大電力伝達の値

代替 $R_L = R_{Th}\:\&\:P_L = P_{L, Max}$ 式1で。

$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{(R_{Th} + R_{Th})^2} \rbrace$$

$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{4 {R_{Th}}^2} \rbrace$$

$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$

$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{L}}, \: since \: R_{L} = R_{Th}$$

したがって、 maximum amount of power 負荷に転送されます

$$P_{L, Max} = \frac{{V_{Th}}^2}{4R_{L}} = \frac{{V_{Th}}^2}{4R_{Th}}$$

最大電力伝達の効率

最大電力伝達の効率を計算できます。 $\eta_{Max}$ 次の式を使用します。

$\eta_{Max} = \frac{P_{L, Max}}{P_S}$ Equation 2

どこ、

• $P_{L, Max}$ は、負荷に転送される電力の最大量です。

• $P_S$ ソースによって生成された電力量です。

ザ・ amount of power generated ソースによってです

$$P_S = I^2 R_{Th} + I^2 R_L$$

$$\Rightarrow P_S = 2 I^2 R_{Th},\:since\:R_{L} = R_{Th}$$

• 代替 $I = \frac{V_{Th}}{2 R_{Th}}$ 上記の式で。

$$P_S = 2\lgroup \frac{V_{Th}}{2 R_{Th}} \rgroup ^2 R_{Th}$$

$$\Rightarrow P_S = 2\lgroup \frac{{V_{Th}}^2}{4 {R_{Th}}^2} \rgroup R_{Th}$$

$$\Rightarrow P_S = \frac{{V_{Th}}^2}{2 R_{Th}}$$

• の値を代入します $P_{L, Max}$ そして $P_S$ 式2で。

$$\eta_{Max} = \frac{\lgroup \frac{{V_{Th}}^2}{4R_{Th}} \rgroup}{\lgroup \frac{{V_{Th}}^2}{2R_{Th}}\rgroup}$$

$$\Rightarrow \eta_{Max} = \frac{1}{2}$$

最大電力伝達の効率を次のように表すことができます。 percentage 次のように-

$$\% \eta_{Max} = \eta_{Max} \times 100\%$$

$$\Rightarrow \% \eta_{Max} = \lgroup \frac{1}{2} \rgroup \times 100\%$$

$$\Rightarrow \% \eta_{Max} = 50\%$$

したがって、最大電力伝達の効率は次のようになります。 50 %。

例

を見つける maximum powerそれは、負荷抵抗Rに送達することができる_L以下の図に示す回路。

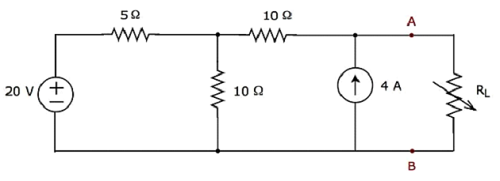
Step 1−テブナンの定理の章では、端子AとBの左側にあるテブナンの等価回路を計算しました。これでこの回路を使用できます。次の図に示します。

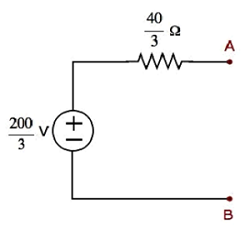
ここで、テブナンの電圧 $V_{Th} = \frac{200}{3}V$ テブナンの抵抗 $R_{Th} = \frac{40}{3} \Omega$

Step 2−所定の回路の端子AとBの左側にある回路の部分を、上記のテブナンの等価回路に置き換えます。結果の回路図を次の図に示します。

Step 3-我々は、負荷抵抗Rに配信される最大電力見つけることができる_L以下の式を使用しています。

$$P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$

代替 $V_{Th} = \frac{200}{3}V$ そして $R_{Th} = \frac{40}{3} \Omega$ 上記の式で。

$$P_{L, Max} = \frac{\lgroup \frac{200}{3} \rgroup ^ 2}{4 \lgroup \frac{40}{3}\rgroup } $$

$$P_{L, Max} = \frac{250}{3} W$$

したがって、 maximum power 与えられた回路の負荷抵抗RLに供給されるのは $\mathbf {\frac{250}{3}}$ W

入力用の電気回路の出力が時間に対して変化する場合、それは次のように呼ばれます。 time response。時間応答は、次の2つの部分で構成されます。

• 過渡応答
• 定常状態の応答

この章では、最初にこれら2つの応答について説明し、次にDC電圧源によって励起されたときの直列RL回路でこれら2つの応答を観察します。

過渡応答

電気回路に入力を加えた後、出力が定常状態に達するまでに一定の時間がかかります。したがって、出力は定常状態になるまで過渡状態になります。したがって、過渡状態の間の電気回路の応答は、transient response。

't'の値が大きい場合、過渡応答はゼロになります。理想的には、この「t」の値は無限大である必要があります。しかし、実際にはfive time constants 十分です。

トランジェントの有無

一時的なものは、 sudden change電気回路に適用される、および/またはスイッチング動作によるソース内。2つの可能な切り替えアクションがあります。それらは開閉スイッチです。

• ザ・ transient 一部は not present電気回路またはネットワークの応答で、抵抗のみが含まれている場合。なぜならresistor 電圧と電流の量を調整する機能があります。

• ザ・ transient part occurs 次のようなエネルギー貯蔵要素の存在による電気回路またはネットワークの応答 inductor and capacitor。それらの要素に蓄えられたエネルギーを即座に変えることができないからです。

インダクタの動作

切り替え動作がt = 0で行われると仮定します。Inductor current切り替え動作が発生しても、瞬時には変化しません。つまり、スイッチング動作直後のインダクタ電流の値は、スイッチング動作直前のインダクタ電流の値と同じになります。

数学的には、次のように表すことができます。

$$i_L (0^+) = i_L (0^-)$$

コンデンサの動作

ザ・ capacitor voltageスイッチング動作が発生しても、インダクタ電流のように瞬時に変化することはありません。つまり、スイッチング動作直後のコンデンサ電圧の値は、スイッチング動作直前のコンデンサ電圧の値と同じになります。

数学的には、次のように表すことができます。

$$v_c (0^+) = v_c (0^-)$$

定常状態の応答

't'の値が大きい場合に過渡応答がゼロ値になった後も残る時間応答の部分は、次のように知られています。 steady state response。これは、定常状態での応答に一時的な部分がないことを意味します。

インダクタの動作

独立した電源が、1つまたは複数のインダクタと抵抗（オプション）を備えた電気回路またはネットワークに長時間接続されている場合、その電気回路またはネットワークは定常状態にあると言われます。したがって、その電気回路のインダクタに蓄えられるエネルギーは最大で一定です。

数学的には、次のように表すことができます。

$W_L = \frac{L {i_L}^2}{2} = $ 最大＆定数

$\Rightarrow i_L = $ 最大＆定数

したがって、インダクタは constant current source 定常状態で。

インダクタ両端の電圧は

$$V_L = L \frac{di_{L}}{dt} = 0V$$

したがって、インダクタは short circuit 定常状態で。

コンデンサの動作

独立した電源が、1つまたは複数のコンデンサと抵抗（オプション）を備えた電気回路またはネットワークに長時間接続されている場合、その電気回路またはネットワークは定常状態にあると言われます。したがって、その電気回路のコンデンサに蓄えられるエネルギーは最大で一定です。

数学的には、次のように表すことができます。

$W_c = \frac{C{v_c}^2}{2} = $ 最大＆定数

$\Rightarrow v_c = $最大＆定数

したがって、コンデンサは constant voltage source 定常状態で。

コンデンサに流れる電流は

$$i_c = C\frac{dv_c}{dt} = 0A$$

したがって、コンデンサは open circuit 定常状態で。

シリーズRL回路の応答を見つける

次のことを考慮してください series RL circuit 図。

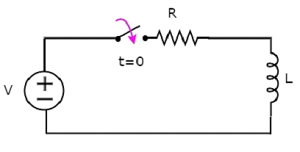
上記の回路では、 switch 保たれた opent = 0までで、t = 0で閉じられました。したがって、VボルトのDC電圧源は、この瞬間まで直列RL回路に接続されていません。したがって、no initial current インダクタを流れます。

回路図、 switch にあります closed 位置を次の図に示します。

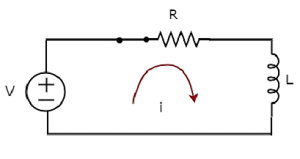
今、現在 i DC電圧源が持っているので、回路全体に流れます V ボルトは直列RL回路に接続されています。

今、適用します KVL ループの周り。

$$V = Ri + L \frac{di}{dt}$$

$\frac{di}{dt} + \lgroup \frac{R}{L} \rgroup i = \frac{V}{L}$Equation 1

上記の方程式は一階微分方程式であり、次の形式になります。

$\frac{dy}{dt} + Py = Q$Equation 2

沿って comparing 式1と式2では、次の関係が得られます。

$$x = t$$

$$y = i$$

$$P = \frac{R}{L}$$

$$Q = \frac{V}{L}$$

ザ・ solution 式2の

$ye^{\int p dx} = \int Q e^{\int p dx} dx + k$Equation 3

どこ、 k は定数です。

式3のx、y、P、Qの値を代入します。

$ie^{\int {\lgroup \frac{R}{L} \rgroup}dt} = \int (\frac{V}{L}) \lgroup e^{\int {\lgroup \frac{R}{L} \rgroup}dt} \rgroup dt + k$

$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \int e^{\lgroup \frac{R}{L} \rgroup t} dt + k$

$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \lbrace \frac{e^{\lgroup \frac{R}{L} \rgroup}t}{\frac{R}{L}} \rbrace + k$

$\Rightarrow i = \frac{V}{R} + k e^{-\lgroup \frac{R}{L} \rgroup}t$Equation 4

回路には初期電流がないことがわかっています。したがって、t = 0および 定数の値を見つけるために式4で= 0 k。

$$0 = \frac{V}{R} + ke^{-\lgroup \frac{R}{L} \rgroup(0)}$$

$$0 = \frac{V}{R} + k(1)$$

$$k = - \frac{V}{R}$$

式4のkの値を代入します。

$$i = \frac{V}{R} + \lgroup - \frac{V}{R} \rgroup e^{-\lgroup \frac{R}{L} \rgroup t}$$

$$i = \frac{V}{R} - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$$

したがって、 current 回路を流れるのは

$i = - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t} + \frac{V}{R}$Equation 5

したがって、直列RL回路の応答は、DC電圧源によって励起された場合、次の2つの項があります。

• 第一期 $-\frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$ に対応 transient response。

• 第2期 $\frac{V}{R}$ に対応 steady state response。これらの2つの応答を次の図に示します。

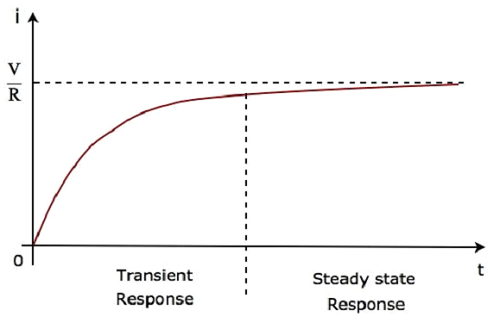
式5は次のように書き直すことができます。

$i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{R}{L} \rgroup t} \rgroup$

$\Rightarrow i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{t}{\tau} \rgroup} \rgroup$Equation 6

どこ、 τ それは time constant そしてその値はに等しい $\frac{L}{R}$。

式5と式6はどちらも同じです。しかし、式6から回路を流れる電流の上記の波形は、次のいくつかの値を代入することで簡単に理解できます。t 0、τ、2τ、5τなどのように。

上記の回路を流れる電流の波形では、過渡応答はゼロから最大5つの時定数を示しますが、定常状態の応答は5つの時定数以降を示します。

前の章では、DC回路の過渡応答と定常応答について説明しました。この章では、response of AC circuit。前の章で説明した過渡応答と定常状態応答の両方の概念は、ここでも役立ちます。

シリーズRL回路の応答を見つける

次のことを考慮してください series RL circuit 図。

上記の回路では、 switch 保たれた openまで、T = 0とそれがで閉鎖されたT = 0。したがって、ピーク電圧がV _mボルトのAC電圧源は、この時点まで直列RL回路に接続されていません。したがって、no initial current インダクタを流れます。

回路図、 switch にあります closed 位置は、次の図に示されています。

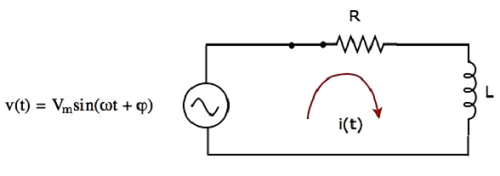
ここで、V _mボルトのピーク電圧を持つAC電圧源が直列RL回路に接続されているため、電流i（t）が回路全体に流れます。

上記の回路を流れる電流i（t）には、過渡部分を表す項と定常状態を表す項の2つの項があることがわかっています。

数学的には、次のように表すことができます。

$i(t) = i_{Tr}(t) + i_{ss}(t)$Equation 1

どこ、

• $i_{Tr}(t)$ は回路を流れる電流の過渡応答です。

• $i_{ss}(t)$ は、回路を流れる電流の定常状態応答です。

前の章では、直列RL回路を流れる電流の過渡応答を取得しました。それはの形です$Ke^{-\lgroup \frac{t}{\tau} \rgroup}$。

代替 $i_{Tr}(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup}$ 式1で。

$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + i_{ss}(t)$Equation 2

定常電流の計算

正弦波信号が線形電気回路への入力として適用されると、定常状態の出力が生成されます。これは、 sinusoidal signal。入力と出力の両方の正弦波信号は同じ周波数を持ちますが、振幅と位相角は異なります。

電気回路が正弦波電圧源によって励起されたときの定常状態応答は、次を使用して計算できます。 Laplace Transform approach。

sドメイン回路図、 switch にあります closed 位置は、次の図に示されています。

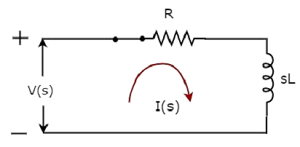
上記の回路では、すべての量とパラメータは次のように表されます。 s-domain。これらは、時間領域の量とパラメーターのラプラス変換です。

ザ・ Transfer function 上記の回路の

$$H(s) = \frac{I(s)}{V(s)}$$

$$\Rightarrow H(s) = \frac{1}{Z(s)}$$

$$\Rightarrow H(s) = \frac{1}{R + sL}$$

代替 $s = j \omega$ 上記の式で。

$$H(j \omega) = \frac{1}{R + j \omega L}$$

Magnitude of $\mathbf{\mathit{H(j \omega)}}$ です

$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2}L^2}$$

Phase angle of $\mathbf{\mathit{H(j \omega)}}$ です

$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} \rgroup$$

取得します steady state current $i_{ss}(t)$ 次の2つのステップを実行することによって-

• 入力正弦波電圧のピーク電圧との大きさを乗算します $H(j \omega)$。

• 入力正弦波電圧の位相角を追加し、 $H(j \omega)$。

ザ・ steady state current $i_{ss}(t)$ になります

$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

の値を代入します $i_{ss}(t)$ 式2で。

$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 3

回路には初期電流がないことがわかっています。したがって、定数Kの値を見つけるには、式3にt = 0＆i（t）= 0を代入します。

$$0 = Ke^{-\lgroup \frac{0}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

式3にKの値を代入します。

$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup e^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 4

式4は、正弦波電圧源によって励起されたときに直列RL回路を流れる電流を表しています。それは2つの用語を持っています。第1項と第2項は、それぞれ電流の過渡応答と定常状態応答を表します。

私たちはできる neglect the first termその値は1より非常に小さいため、式4の したがって、回路を流れる結果として生じる電流は次のようになります。

$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

のみが含まれています steady state term。したがって、AC回路の定常応答のみを見つけ、その過渡応答を無視することができます。

Resonanceインダクタやコンデンサなどのエネルギー蓄積要素の存在により、電気回路で発生します。これは基本的な概念であり、ラジオとテレビの受信機は、希望する局の周波数のみを選択できるように設計されています。

がある two types共振、すなわち直列共振と並列共振の。これらは、直列または並列に接続されているネットワーク要素に基づいて分類されます。この章では、直列共振について説明します。

直列共振回路図

直列RLC回路で共振が発生する場合、それは次のように呼ばれます。 Series Resonance。次のことを考慮してくださいseries RLC circuit、これはフェーザドメインで表されます。

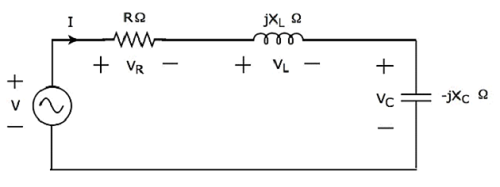
ここでは、抵抗、インダクタ、コンデンサなどの受動素子が直列に接続されています。この全体の組み合わせはseries 入力正弦波電圧源を使用します。

適用する KVL ループの周り。

$$V - V_R - V_L - V_C = 0$$

$$\Rightarrow V - IR - I(j X_L) - I(-j X_C) = 0$$

$$\Rightarrow V = IR + I(j X_L) + I(-j X_C)$$

$\Rightarrow V = I[R + j(X_L - X_C)]$Equation 1

上記の式は次の形式です。 V = IZ。

したがって、 impedance Z シリーズRLC回路の

$$Z = R + j(X_L - X_C)$$

共振時のパラメータと電気量

ここで、直列RLC回路の共振時のパラメータと電気量の値を1つずつ導き出します。

共鳴周波数

共振が発生する周波数は、 resonant frequency f_r。直列RLC回路の共振は、インピーダンスZの虚数項がゼロのときに発生します。$X_L - X_C$ ゼロに等しくなければなりません。

$$\Rightarrow X_L = X_C$$

代替 $X_L = 2 \pi f L$ そして $X_C = \frac{1}{2 \pi f C}$ 上記の式で。

$$2 \pi f L = \frac{1}{2 \pi f C}$$

$$\Rightarrow f^2 = \frac{1}{(2 \pi)^2 L C}$$

$$\Rightarrow f = \frac{1}{(2 \pi) \sqrt{LC}}$$

したがって、 resonant frequency f_r シリーズRLC回路の

$$f_r = \frac{1}{(2 \pi) \sqrt{LC}}$$

どこ、 L はインダクタのインダクタンスであり、 C はコンデンサの静電容量です。

ザ・ resonant frequency f_r 直列RLC回路のインダクタンスのみに依存します L と静電容量 C。しかし、それは抵抗とは無関係ですR。

インピーダンス

私たちは impedance Z シリーズRLC回路の

$$Z = R + j(X_L - X_C)$$

代替 $X_L = X_C$ 上記の式で。

$$Z = R + j(X_C - X_C)$$

$$\Rightarrow Z = R + j(0)$$

$$\Rightarrow Z = R$$

共鳴すると、 impedance Z 直列RLC回路の抵抗値に等しい R、すなわち、 Z = R。

回路を流れる電流

代替 $X_L - X_C = 0$ 式1で。

$$V = I[R + j(0)]$$

$$\Rightarrow V = IR$$

$$\Rightarrow I = \frac{V}{R}$$

したがって、 current 共振時に直列RLC回路を流れるのは $\mathbf{\mathit{I = \frac{V}{R}}}$。

共振時、直列RLC回路のインピーダンスは最小値に達します。従ってmaximum current 共振時にこの回路を流れます。

抵抗器の両端の電圧

抵抗の両端の電圧は

$$V_R = IR$$

の値を代入します I 上記の式で。

$$V_R = \lgroup \frac{V}{R} \rgroup R$$

$$\Rightarrow V_R = V$$

したがって、 voltage across resistor 共振時は V_R = V。

インダクタ両端の電圧

インダクタ両端の電圧は

$$V_L = I(jX_L)$$

の値を代入します I 上記の式で。

$$V_L = \lgroup \frac{V}{R} \rgroup (jX_L)$$

$$\Rightarrow V_L = j \lgroup \frac{X_L}{R} \rgroup V$$

$$\Rightarrow V_L = j QV$$

したがって、 voltage across inductor 共振時は $V_L = j QV$。

だから、 magnitude 共振時のインダクタ両端の電圧は

$$|V_L| = QV$$

どこ Q それは Quality factor そしてその値はに等しい $\frac{X_L}{R}$

コンデンサ両端の電圧

コンデンサ両端の電圧は

$$V_C = I(-j X_C)$$

上記の式にIの値を代入します。

$$V_C = \lgroup \frac{V}{R} \rgroup (-j X_C)$$

$$\Rightarrow V_C = -j \lgroup \frac{X_C}{R} \rgroup V$$

$$\Rightarrow V_C = -jQV$$

したがって、 voltage across capacitor 共振時は $\mathbf{\mathit{V_C = -jQV}}$。

だから、 magnitude 共振時のコンデンサ両端の電圧は

$$|V_C| = QV$$

どこ Q それは Quality factor そしてその値はに等しい $\frac{X_{C}}{R}$

Note −直列共振RLC回路は次のように呼ばれます voltage magnificationインダクタとコンデンサの両端の電圧の大きさは、入力正弦波電圧VのQ倍に等しいためです。

前の章では、直列共振の重要性について説明しました。それでは、RLC回路の並列共振について説明しましょう。

並列共振回路図

並列RLC回路で共振が発生する場合、それは次のように呼ばれます。 Parallel Resonance。次のことを考慮してくださいparallel RLC circuit、これはフェーザドメインで表されます。

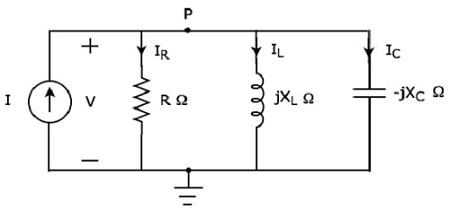
ここでは、抵抗、インダクタ、コンデンサなどの受動素子が並列に接続されています。この全体の組み合わせはparallel 入力正弦波電流源を使用します。

書く nodal equation ノードPで。

$$- I + I_R + I_L + I_C = 0$$

$$\Rightarrow - I + \frac{V}{R} + \frac{V}{j X_L} + \frac{V}{-j X_C} = 0$$

$$\Rightarrow I = \frac{V}{R} - \frac{jV}{X_L} + \frac{jV}{X_C}$$

$\Rightarrow I = V[\frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup]$Equation 1

上記の式は次の形式です。 I = VY。

したがって、 admittance Y 並列RLC回路の

$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$

共振時のパラメータと電気量

ここで、並列RLC回路の共振時のパラメータと電気量の値を1つずつ導き出します。

共鳴周波数

私たちは、 resonant frequency, f_rは、共振が発生する周波数です。並列RLC回路では、アドミタンスの虚数項Yがゼロのときに共振が発生します。つまり、$\frac{1}{X_C} - \frac{1}{X_L}$ ゼロに等しくなければなりません

$$\Rightarrow \frac{1}{X_C} = \frac{1}{X_L}$$

$$\Rightarrow X_L = X_C$$

上記の共振条件は直列RLC回路と同じです。だから、resonant frequency, f_r 直列RLC回路と並列RLC回路の両方で同じになります。

したがって、 resonant frequency, f_r 並列RLC回路の

$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$

どこ、

• Lはインダクタのインダクタンスです。
• Cはコンデンサの静電容量です。

ザ・ resonant frequency, f_r 並列RLC回路のインダクタンスのみに依存します L と静電容量 C。しかし、それは抵抗とは無関係ですR。

アドミタンス

私たちは admittance Y 並列RLC回路の

$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$

代替、 $X_L = X_C$ 上記の式で。

$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_C} \rgroup$$

$$\Rightarrow Y = \frac{1}{R} + j(0)$$

$$\Rightarrow Y = \frac{1}{R}$$

共鳴すると、 admittance、並列RLC回路のYは、抵抗の逆数Rに等しくなります。 $\mathbf{\mathit{Y = \frac{1}{R}}}$

各要素の両端の電圧

代替、 $\frac{1}{X_C} - \frac{1}{X_L} = 0$ 式1で

$$I = V [\frac{1}{R} + j(0)]$$

$$\Rightarrow I = \frac{V}{R}$$

$$\Rightarrow V = IR$$

したがって、 voltage 共振時の並列RLC回路のすべての要素にわたって V = IR。

共振時に、並列RLC回路のアドミタンスは最小値に達します。したがって、maximum voltage 共振時にこの回路の各要素に存在します。

抵抗器を流れる電流

抵抗を流れる電流は

$$I_R = \frac{V}{R}$$

の値を代入します V 上記の式で。

$$I_R = \frac{IR}{R}$$

$$\Rightarrow I_R = I$$

したがって、 current flowing through resistor 共振時は $\mathbf{\mathit{I_R = I}}$。

インダクタを流れる電流

インダクタを流れる電流は

$$I_L = \frac{V}{j X_L}$$

の値を代入します V 上記の式で。

$$I_L = \frac{IR}{j X_L}$$

$$\Rightarrow I_L = -j \lgroup \frac{R}{X_L} \rgroup I$$

$$\Rightarrow I_L = -jQI$$

したがって、 current flowing through inductor 共振時は $I_L = -jQI$。

だから、 magnitude 共振時にインダクタを流れる電流の

$$|I_L| = QI$$

ここで、Qは Quality factor そしてその値はに等しい $\frac{R}{X_L}$

コンデンサを流れる電流

コンデンサを流れる電流は

$$I_C = \frac{V}{-j X_C}$$

の値を代入します V 上記の式で。

$$I_C = \frac{IR}{-j X_C}$$

$$\Rightarrow I_C = j \lgroup \frac{R}{X_C} \rgroup I$$

$$\Rightarrow I_C = jQI$$

したがって、 current flowing through capacitor 共振時は $I_C = jQI$

だから、 magnitude 共振時にコンデンサを流れる電流の

$$|I_C| = QI$$

ここで、Qは Quality factor そしてその値はに等しい $\frac{R}{X_C}$

Note −並列共振RLC回路は current magnification回路。なぜなら、インダクタとコンデンサを流れる電流の大きさは、入力正弦波電流IのQ倍に等しいからです。

電気回路は coupled circuit、その回路に存在するコイル（またはインダクタ）間に相互インダクタンスが存在する場合。コイルは、抵抗とインダクタの直列の組み合わせに他なりません。抵抗がない場合、コイルはインダクタになります。コイルとインダクタという用語は同じ意味で使用されることがあります。

この章では、最初にドットの規則について説明し、次に結合の分類について説明します。

ドットコンベンション

ドット規則は、ドット端子の電圧極性に関する詳細を提供する手法です。この情報は、KVL方程式を作成するときに役立ちます。

• あるコイル（またはインダクター）の点線の端子に電流が入ると、別のコイル（またはインダクター）に電圧が誘導されます。 positive polarity 点線のターミナルで。

• あるコイル（またはインダクター）の点線の端子から電流が出ると、別のコイル（またはインダクター）に電圧が誘導されます。 negative polarity 点線のターミナルで。

カップリングの分類

分類できます coupling 次の2つのカテゴリに分類されます。

• 電気的結合
• 磁気結合

それでは、それぞれのタイプのカップリングについて1つずつ説明しましょう。

電気的結合

電気的結合は、 physical connection2つのコイル（またはインダクタ）の間。このカップリングは、補助タイプまたは反対タイプのいずれかです。これは、電流が点線の端子から入るか、点線の端子から出るかに基づいています。

補助タイプのカップリング

次の電気回路を考えてみましょう。この回路には、2つのインダクタが接続されています。 series。

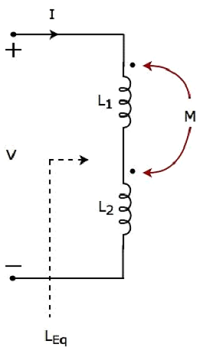
2つのインダクタが直列に接続されているため、 same current I自己インダクタンスLを有するインダクタの両方を通って流れ₁及びL ₂。

この場合、電流は各インダクタの点線の端子から入ります。したがって、各インダクタの誘導電圧は次のようになります。positive polarity 別のコイルに電流が流れるため、点線の端子で。

適用する KVL 上記の電気回路またはネットワークのループの周り。

$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$

$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$

$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$

上記の式は次の形式です。 $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

したがって、 equivalent inductance 上図に示すインダクタの直列組み合わせの

$$L_{Eq} = L_1 + L_2 + 2M$$

この場合、等価インダクタンスは2M増加しています。したがって、上記の電気回路はelectrical のカップリング aiding タイプ。

対向型のカップリング

次の電気回路を考えてみましょう。この回路には、2つのインダクタが接続されています。 series。

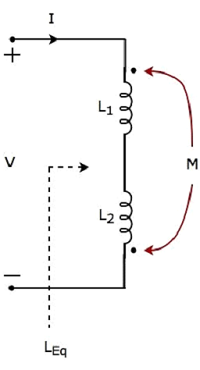
上記の回路では、電流 I のインダクタンスを持つインダクタの点線の端子から入ります L₁。したがって、インダクタンスが次のインダクタに電圧を誘導します。L₂。そう、positive polarity 誘導電圧のは、このインダクタの点線の端子に存在します。

上記の回路では、電流 I のインダクタンスを持つインダクタの点線の端子から離れます L₂。したがって、インダクタンスが次のインダクタに電圧を誘導します。L₁。そう、negative polarity 誘導電圧のは、このインダクタの点線の端子に存在します。

適用する KVL 上記の電気回路またはネットワークのループの周り。

$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$

$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$

$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$

上記の式は次の形式です。 $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

したがって、 equivalent inductance 上図に示すインダクタの直列組み合わせの

$$L_{Eq} = L_1 + L_2 - 2M$$

この場合、等価インダクタンスは2M減少しています。したがって、上記の電気回路はelectrical のカップリング opposing タイプ。

磁気結合

磁気結合が発生すると、 no physical connection2つのコイル（またはインダクタ）の間。このカップリングは、補助タイプまたは反対タイプのいずれかです。これは、電流が点線の端子から入るか、点線の端子から出るかに基づいています。

補助タイプのカップリング

次の電気的同等物を検討してください circuit of transformer。それは2つのコイルを持っており、これらは一次コイルと二次コイルと呼ばれます。

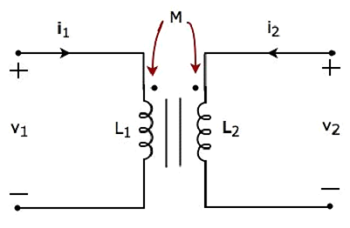
一次および二次コイルに流れる電流はIである₁とI ₂をそれぞれ。この場合、これらの電流enterそれぞれのコイルの点線の端子で。したがって、各コイルの誘導電圧は、別のコイルに電流が流れるため、点線の端子で正極性になります。

適用する KVL 一次コイルの周り。

$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$Equation 1

適用する KVL 二次コイルの周り。

$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$Equation 2

式1と式2では、自己誘導電圧と相互誘導電圧は同じ極性を持っています。したがって、上記のトランス回路はmagnetic coupling、の aiding タイプ。

反対型のカップリング

次の電気的同等物を検討してください circuit of transformer。

一次および二次コイルに流れる電流はIである₁とI ₂をそれぞれ。この場合、電流は、I _1は、一次コイルのドット端末に入ります。したがって、2次コイルに電圧を誘導します。そう、positive polarity 誘導電圧のは、この二次コイルの点線の端子に存在します。

上記回路において、電流、I ₂二次コイルのドット端末からの葉。したがって、一次コイルに電圧を誘導します。そう、negative polarity 誘導電圧のは、この一次コイルの点線の端子に存在します。

適用する KVL 一次コイルの周り。

$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$Equation 3

適用する KVL 二次コイルの周り。

$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$Equation 4

式3と式4では、自己誘導電圧と相互誘導電圧の極性が逆になっています。したがって、上記のトランス回路はmagnetic coupling、の opposing タイプ。

一般に、入力変数と出力変数の関係を示す同等のモデルで表されている場合、電気ネットワークを分析するのは簡単です。このために、私たちは使用することができますtwo port network表現。名前が示すように、2つのポートネットワークには2つのポートが含まれています。このうち、一方のポートは入力ポートとして使用され、もう一方のポートは出力ポートとして使用されます。1番目と2番目のポートは、それぞれport1とport2と呼ばれます。

One port networkは2端子の電気ネットワークで、電流は1つの端子から入り、別の端子から出ます。抵抗、インダクタ、コンデンサは、それぞれに2つの端子があるため、1つのポートネットワークの例です。次の図に、1つのポートネットワーク表現を示します。

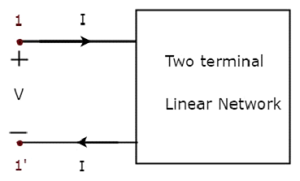
ここで、端子のペア1＆1 'はポートを表します。この場合、1ポートネットワークであるため、ポートは1つだけです。

同様に、 two port networkは2端子電気ネットワークのペアであり、電流は各ポートの1つの端子から入り、別の端子から出ます。次の図に、2ポートネットワークの表現を示します。

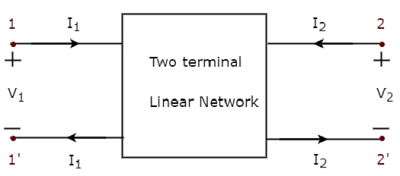
ここで、1対の端子1＆1 'は、1つのポートを表します。 port1 もう一方の端子のペアである2＆2 'は、次のように呼ばれる別のポートを表します。 port2。

がある four variablesV ₁、V ₂、I ₁及びI ₂ 2つのポートネットワークの図に示すように。そのうち、2つの変数を独立変数として選択し、別の2つの変数を従属変数として選択できます。したがって、6つの可能な方程式のペアを取得します。これらの方程式は、独立変数の観点から従属変数を表します。独立変数の係数は次のように呼ばれますparameters。したがって、方程式の各ペアは4つのパラメーターのセットを提供します。

2つのポートネットワークパラメータ

2ポートネットワークのパラメータは次のように呼ばれます two port network parametersまたは単に、2つのポートパラメータ。以下は、2つのポートネットワークパラメータのタイプです。

• Zパラメータ
• Yパラメータ
• Tパラメータ
• T 'パラメータ
• h-parameters
• g-parameters

ここで、これら2つのポートネットワークパラメータについて1つずつ説明します。

Zパラメータ

私たちは、変数V考慮することにより、2つの以下の式のセットを取得します₁＆V ₂に依存し、私のように₁＆I ₂の独立したとしてを。独立変数の係数は、I ₁及びI _2は、と呼ばれていますZ parameters。

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

ザ・ Z parameters です

$$Z_{11} = \frac{V_1}{I_1}, \: when \: I_2 = 0$$

$$Z_{12} = \frac{V_1}{I_2}, \: when \: I_1 = 0$$

$$Z_{21} = \frac{V_2}{I_1}, \: when \: I_2 = 0$$

$$Z_{22} = \frac{V_2}{I_2}, \: when \: I_1 = 0$$

Zパラメータは次のように呼ばれます impedance parametersこれらは単に電圧と電流の比率だからです。Zパラメータの単位はオーム（Ω）です。

我々は2つのZパラメータ、Zを計算することができます₁₁およびZ _21のポート2の開放を行うことによって、。同様に、我々は、他の2つのZパラメータ、Z計算することができる₁₂およびZ _22のPORT1の開回路の操作を行って。したがって、Zパラメータは次のようにも呼ばれます。open-circuit impedance parameters。

Yパラメータ

私たちは、私の変数考慮して2つの以下の式のセットを取得します₁＆I ₂依存などとV ₁＆V ₂として独立を。独立変数の係数、V ₁及びV _2は、と呼ばれていますY parameters。

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

ザ・ Y parameters です

$$Y_{11} = \frac{I_1}{V_1}, \: when \: V_2 = 0$$

$$Y_{12} = \frac{I_1}{V_2}, \: when \: V_1 = 0$$

$$Y_{21} = \frac{I_2}{V_1}, \: when \: V_2 = 0$$

$$Y_{22} = \frac{I_2}{V_2}, \: when \: V_1 = 0$$

Yパラメータは次のように呼ばれます admittance parametersこれらは単純に、電流と電圧の比率だからです。Yパラメータの単位はモーです。

我々は2つのYパラメータ、Yを計算することができます₁₁及びY _21のポート2の短絡を行うことで。同様に、我々は、他の2つのYパラメーター、Y計算することができる₁₂及びY _22のPORT1の短絡を行うことによって。したがって、Yパラメータは次のようにも呼ばれます。short-circuit admittance parameters。

Tパラメータ

私たちは、変数を考慮することにより、2つの以下の式のセットを取得しますV ₁＆I ₁依存などとV ₂＆I _2を独立したとして。Vの係数₂及び-I _2はと呼ばれT parameters。

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

ザ・ T parameters です

$$A = \frac{V_1}{V_2}, \: when \: I_2 = 0$$

$$B = -\frac{V_1}{I_2}, \: when \: V_2 = 0$$

$$C = \frac{I_1}{V_2}, \: when \: I_2 = 0$$

$$D = -\frac{I_1}{I_2}, \: when \: V_2 = 0$$

Tパラメータは送信パラメータまたは ABCD parameters。パラメータAとDは次元が少ないため、単位はありません。パラメータの単位BとCは、それぞれオームとモーです。

ポート2を開回路にすることで、AとCの2つのパラメータを計算できます。同様に、port2を短絡することにより、他の2つのパラメータBとDを計算できます。

T 'パラメータ

私たちは、変数V考慮することにより、2つの以下の式のセットを取得します₂＆I ₂依存やVなど₁＆I ₁として独立を。Vの係数₁及び-I ₁と呼ばれT’ parameters。

$$V_2 = A' V_1 - B' I_1$$

$$I_2 = C' V_1 - D' I_1$$

ザ・ T’ parameters です

$$A' = \frac{V_2}{V_1}, \: when\: I_1 = 0$$

$$B' = -\frac{V_2}{I_1}, \: when\: V_1 = 0$$

$$C' = \frac{I_2}{V_1}, \: when\: I_1 = 0$$

$$D' = -\frac{I_2}{I_1}, \: when \: V_1 = 0$$

T 'パラメータは逆伝送パラメータまたは A’B’C’D’ parameters。パラメータA 'とD'は次元が少ないため、単位はありません。パラメータの単位であるB 'とC'は、それぞれオームとモーです。

port1の開回路を実行することにより、2つのパラメーターA 'とC'を計算できます。同様に、port1を短絡することにより、他の2つのパラメーターB 'とD'を計算できます。

hパラメータ

私たちは、変数V考慮することにより、2つの以下の式のセットを取得します₁＆I ₂依存とIとして₁＆V ₂として独立を。独立変数の係数は、I ₁及びV ₂、と呼ばれていますh-parameters。

$$V_1 = h_{11} I_1 + h_{12} V_2$$

$$I_2 = h_{21} I_1 + h_{22} V_2$$

hパラメータは

$$h_{11} = \frac{V_1}{I_1},\: when\: V_2 = 0$$

$$h_{12} = \frac{V_1}{V_2},\: when\: I_1 = 0$$

$$h_{21} = \frac{I_2}{I_1},\: when\: V_2 = 0$$

$$h_{22} = \frac{I_2}{V_2},\: when\: I_1 = 0$$

hパラメータは次のように呼ばれます hybrid parameters。パラメータ、H ₁₂及びH _21は、それらが寸法以下であるため、任意の単位を持っていません。パラメータの単位、H ₁₁及びH _22は、それぞれ、オームとモーです。

我々は、2つのパラメータ、時間計算することができる₁₁及びh _21をPORT2の短絡を行うことによって。同様に、我々は、他の2つのパラメータ、時間計算することができる₁₂及びh _22をポート1の開回路の操作を行って。

hパラメータまたはハイブリッドパラメータは、トランジスタモデリング回路（ネットワーク）で役立ちます。

gパラメータ

私たちは、変数I考慮して2つの以下の式のセットを取得します₁＆V ₂に依存するようにしてV ₁＆I ₂の独立したとしてを。独立変数の係数、V ₁及びI _2は、と呼ばれていますg-parameters。

$$I_1 = g_{11} V_1 + g_{12} I_2$$

$$V_2 = g_{21} V_1 + g_{22} I_2$$

ザ・ g-parameters です

$$g_{11} = \frac{I_1}{V_1},\: when\: I_2 = 0$$

$$g_{12} = \frac{I_1}{I_2},\: when\: V_1 = 0$$

$$g_{21} = \frac{V_2}{V_1},\: when\: I_2 = 0$$

$$g_{22} = \frac{V_2}{I_2},\: when \: V_1 = 0$$

gパラメータは次のように呼ばれます inverse hybrid parameters。パラメータは、G ₁₂及びG _21は、それらが以下の寸法であるので、任意単位を有していません。パラメータの単位は、G ₁₁及びG _22は、それぞれ、モーとオームです。

我々は2つのパラメータ、グラム計算することができ₁₁とg _21のポート2の開放を行うことで。同様に、我々は、他の2つのパラメータ、G計算することができる₁₂及びG _22をポート1の短絡を行うことによって。

前の章では、6種類の2ポートネットワークパラメータについて説明しました。ここで、2ポートネットワークパラメータの1つのセットを2ポートネットワークパラメータの別のセットに変換してみましょう。この変換は、2ポートネットワークパラメータ変換または単に、two-port parameters conversion。

特定の電気ネットワークのパラメータの1つのセットを簡単に見つけることが簡単な場合があります。そのような状況では、これらのパラメーターを直接計算する代わりに、これらのパラメーターを必要なパラメーターのセットに変換することができます。

次に、2つのポートパラメータ変換のいくつかについて説明します。

2ポートパラメータ変換の手順

2つのポートネットワークパラメータの一方のセットを2つのポートネットワークパラメータのもう一方のセットに変換しながら、次の手順に従います。

• Step 1 −必要なパラメータの観点から2ポートネットワークの方程式を記述します。

• Step 2 −与えられたパラメータの観点から2ポートネットワークの方程式を記述します。

• Step 3 − Step1の方程式と同様になるように、Step2の方程式を再配置します。

• Step 4−ステップ1とステップ3の同様の方程式を等しくすることにより、与えられたパラメーターに関して目的のパラメーターを取得します。これらのパラメータは行列形式で表すことができます。

ZパラメータからYパラメータ

ここでは、YパラメータをZパラメータで表す必要があります。したがって、この場合、Yパラメーターは目的のパラメーターであり、Zパラメーターは指定されたパラメーターです。

Step 1 −次の2つの方程式のセットは、次の観点から2ポートネットワークを表します。 Y parameters。

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

上記の2つの方程式を次のように表すことができます。 matrix として形

$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 1

Step 2 −次の2つの方程式のセットは、次の観点から2ポートネットワークを表します。 Z parameters。

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

上記の2つの方程式を次のように表すことができます。 matrix として形

$$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$$

Step 3 −次のように変更できます

$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 2

Step 4 −式1と式2を等しくすることにより、次のようになります。

$$\begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} $$

$$\Rightarrow \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \frac{\begin{bmatrix}Z_{22} & -Z_{12} \\-Z_{21} & Z_{11} \end{bmatrix}}{\Delta Z}$$

どこ、

$$\Delta Z = Z_{11} Z_{22} - Z_{12} Z_{21}$$

だから、 inverse of Z parameters matrix、Yパラメータ行列を取得します。

ZパラメータからTパラメータ

ここでは、TパラメータをZパラメータで表す必要があります。したがって、この場合、Tパラメーターは目的のパラメーターであり、Zパラメーターは指定されたパラメーターです。

Step 1 −次の2つの方程式のセットは、次の2つのポートネットワークを表します。 T parameters。

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

Step 2 −次の2つの方程式のセットは、次の観点から2ポートネットワークを表します。 Z parameters。

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

Step 3 −上記の式を次のように修正できます。

$$\Rightarrow V_2 - Z_{22} I_2 = Z_{21} I_1$$

$$\Rightarrow I_1 = \lgroup \frac{1}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{22}}{Z_{21}} \rgroup I_2$$

Step 4 −上記の式は次の形式です。 $I_1 = CV_2 − DI_2$。ここに、

$$C = \frac{1}{Z_{21}}$$

$$D = \frac{Z_{22}}{Z_{21}}$$

Step 5 −代替 $I_1$ ステップ3の値 $V_1$ ステップ2の方程式。

$$V_1 = Z_{11} \lbrace \lgroup \frac {1}{Z_{12}} \rgroup V_2 - \lgroup \frac {Z_{22}}{Z_{21}} \rgroup I_2 \rbrace + Z_{12} I_2$$

$$\Rightarrow V_1 = \lgroup \frac {Z_{11}}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}} \rgroup I_2$$

Step 6 −上記の式は次の形式です。 $V_1 = AV_2 − BI_2$。ここに、

$$A = \frac{Z_{11}}{Z_{21}}$$

$$B = \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}}$$

Step 7 −したがって、 T parameters matrix です

$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{Z_{11}}{Z_{21}} & \frac{Z_{11}Z_{22} - Z_{12}Z_{21}}{Z_{21}} \\\frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}} \end{bmatrix}$$

YパラメータからZパラメータ

ここでは、ZパラメータをYパラメータで表す必要があります。したがって、この場合、Zパラメーターは目的のパラメーターであり、Yパラメーターは指定されたパラメーターです。

Step 1 −Zパラメータに関する2ポートネットワークの次の行列方程式は次のようになります。

$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 3

Step 2 −Yパラメータに関する2ポートネットワークの次の行列方程式は次のようになります。

$$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$$

Step 3 −次のように変更できます

$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 4

Step 4 −式3と式4を等しくすることにより、次のようになります。

$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1}$$

$$\Rightarrow \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \frac{\begin{bmatrix}Y_{22} & - Y_{12} \\- Y_{21} & Y_{11} \end{bmatrix}}{\Delta Y}$$

どこ、

$$\Delta Y = Y_{11} Y_{22} - Y_{12} Y_{21}$$

だから、 inverse of Y parameters matrix、Zパラメータ行列を取得します。

YパラメータからTパラメータ

ここでは、TパラメータをYパラメータで表す必要があります。したがって、この場合、Tパラメーターは目的のパラメーターであり、Yパラメーターは指定されたパラメーターです。

Step 1 −次の2つの方程式のセットは、次の2つのポートネットワークを表します。 T parameters。

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

Step 2 −Yパラメータに関する2ポートネットワークの次の2つの方程式のセットがわかっています。

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

Step 3 −上記の式を次のように修正できます。

$$\Rightarrow I_2 - Y_{22} V_2 = Y_{21} V_1$$

$$\Rightarrow V_1 = \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2$$

Step 4 −上記の式は次の形式です。 $V_1 = AV_2 − BI_2$。ここに、

$$A = \frac{- Y_{22}}{Y_{21}}$$

$$B = \frac{-1}{Y_{21}}$$

Step 5 −代替 $V_1$ ステップ3の値 $I_1$ ステップ2の方程式。

$$I_1 = Y_{11} \lbrace \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2 \rbrace + Y_{12} V_2$$

$$\Rightarrow I_1 = \lgroup \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{- Y_{11}} {Y_{21}} \rgroup I_2$$

Step 6 −上記の式は次の形式です。 $I_1 = CV_2 − DI_2$。ここに、

$$C = \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}}$$

$$D = \frac{- Y_{11}} {Y_{21}}$$

Step 7 −したがって、 T parameters matrix です

$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{-Y_{22}}{Y_{21}} & \frac{-1}{Y_{21}} \\\frac{Y_{12}Y_{21} - Y_{11}Y_{22}}{Y_{21}} & \frac{-Y_{11}}{Y_{21}} \end{bmatrix}$$

Tパラメータからhパラメータへ

ここでは、HパラメータをTパラメータで表す必要があります。したがって、この場合、hparametersは目的のパラメーターであり、Tパラメーターは指定されたパラメーターです。

Step 1 −私たちはそれを知っています、次の h-parameters 2ポートネットワークの。

$$h_{11} = \frac{V_1}{I_1}, \: when \: V_2 = 0$$

$$h_{12} = \frac{V_1}{V_2}, \: when \: I_1 = 0$$

$$h_{21} = \frac{I_2}{I_1}, \: when \: V_2 = 0$$

$$h_{22} = \frac{I_2}{V_2}, \: when \: I_1 = 0$$

Step 2 −次の2ポートネットワークの2つの方程式のセットは T parameters。

$V_1 = A V_2 - B I_2$Equation 5

$I_1 = C V_2 - D I_2$Equation 6

Step 3 −代替 $V_2 = 0$ 上記の式で、2つのhパラメータを見つけるために、 $h_{11}$ そして $h_{21}$。

$$\Rightarrow V_1 = -B I_2$$

$$\Rightarrow I_1 = -D I_2$$

代替、 $V_1$ そして $I_1$ hパラメータの値、 $h_{11}$。

$$h_{11} = \frac{-B I_2}{-D I_2}$$

$$\Rightarrow h_{11} = \frac{B}{D}$$

代替 $I_1$ hパラメータの値 $h_{21}$。

$$h_{21} = \frac{I_2}{- D I_2}$$

$$\Rightarrow h_{21} = - \frac{1}{D}$$

Step 4 −代替 $I_1 = 0$ hパラメータを見つけるためにステップ2の2番目の方程式で $h_{22}$。

$$0 = C V_2 - D I_2$$

$$\Rightarrow C V_2 = D I_2$$

$$\Rightarrow \frac{I_2}{V_2} = \frac{C}{D}$$

$$\Rightarrow h_{22} = \frac{C}{D}$$

Step 5 −代替 $I_2 = \lgroup \frac{C}{D} \rgroup V_2$ hパラメータを見つけるためのステップ2の最初の方程式で、 $h_{12}$。

$$V_1 = A V_2 - B \lgroup \frac{C}{D} \rgroup V_2$$

$$\Rightarrow V_1 = \lgroup \frac{AD - BC}{D} \rgroup V_2$$

$$\Rightarrow \frac{V_1}{V_2} = \frac{AD - BC}{D}$$

$$\Rightarrow h_{12} = \frac{AD - BC}{D}$$

Step 6 −したがって、hパラメータ行列は次のようになります。

$$\begin{bmatrix}h_{11} & h_{12} \\h_{21} & h_{22} \end{bmatrix} = \begin{bmatrix}\frac{B}{D} & \frac{AD - BC}{D} \\-\frac{1}{D} & \frac{C}{D} \end{bmatrix}$$

hパラメータからZパラメータ

ここでは、zパラメータをhパラメータで表す必要があります。したがって、この場合、Zパラメーターは目的のパラメーターであり、hパラメーターは指定されたパラメーターです。

Step 1 −次の2ポートネットワークの2つの方程式のセットは次のとおりです。 Z parameters。

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

Step 2 −次の2ポートネットワークの2つの方程式のセットは次のとおりです。 h-parameters。

$$V_1 = h_{11} I_1 + h_{12} V_2$$

$$I_2 = h_{21} I_1 + h_{22} V_2$$

Step 3 −上記の式を次のように修正できます。

$$\Rightarrow I_2 - h_{21} I_1 = h_{22} V_2$$

$$\Rightarrow V_2 = \frac{I_2 - h_{21} I_1}{h_{22}}$$

$$\Rightarrow V_2 = \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2$$

上記の式は次の形式です。 $V_2 = Z_{21} I_1 + Z_{22} I_2. Here,$

$$Z_{21} = \frac{-h_{21}}{h_{22}}$$

$$Z_{22} = \frac{1}{h_{22}}$$

Step 4-代替V ₂ステップ2の最初の式の値。

$$V_1 = h_{11} I_1 + h_{21} \lbrace \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2 \rbrace$$

$$\Rightarrow V_1 = \lgroup \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{h_{12}}{h_{22}} \rgroup I_2$$

上記の式は次の形式です。 $V_1 = Z_{11}I_1 + Z_{12}I_2$。ここに、

$$Z_{11} = \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}}$$

$$Z_{12} = \frac{h_{12}}{h_{22}}$$

Step 5 −したがって、Zパラメータ行列は次のようになります。

$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}\frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} & \frac{h_{12}}{h_{22}} \\\frac{-h_{21}}{h_{22}} & \frac{1}{h_{22}} \end{bmatrix}$$

このようにして、あるパラメーターのセットを他のパラメーターのセットに変換できます。

名前が示すようにフィルタリングし、周波数成分をフィルタリングします。つまり、特定の周波数成分を許可したり、他の周波数成分を拒否したりします。

この章では、 passive filters。これらは、抵抗、インダクタ、コンデンサなどの受動素子を備えた電気回路またはネットワークです。

フィルタの種類

フィルタは主に次のように分類されます four types許可している周波数の帯域および/または拒否している周波数の帯域に基づいています。フィルタの種類は次のとおりです。

• ローパスフィルタ
• ハイパスフィルタ
• バンドパスフィルター
• バンドストップフィルター

ローパスフィルタ

名前が示すようにローパスフィルター、それは（パス）のみを許可します low frequencyコンポーネント。つまり、他のすべての高周波成分を拒否（ブロック）します。

sドメイン circuit diagram ローパスフィルターの（ネットワーク）を下図に示します。

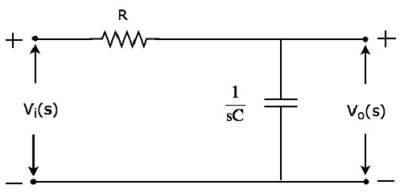
これは、2つの受動素子抵抗とコンデンサで構成されています。 series。入力電圧はこの組み合わせ全体に印加され、出力はコンデンサ両端の電圧と見なされます。

ここに、 $V_i(s)$ そして $V_o(s)$ 入力電圧のラプラス変換です。 $v_i(t)$ および出力電圧、 $v_o(t)$ それぞれ。

ザ・ transfer function 上記のネットワークの

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{\frac{1}{sC}}{R + \frac{1}{sC}}$$

$$\Rightarrow H(s) = \frac{1}{1 + sCR}$$

代替、 $s = j \omega$ 上記の式で。

$$H(j \omega) = \frac{1}{1 + j \omega CR}$$

伝達関数の大きさは

$$|H(j \omega)| = \frac{1}{\sqrt{(1 + (\omega CR)^2}}$$

• でω = 0、伝達関数の大きさは1に等しいです。

• で $\omega = \frac{1}{CR}$、伝達関数の大きさは0.707に等しくなります。

• でω =∞、伝達関数の大きさは0に等しいです。

したがって、の伝達関数の大きさ Low pass filterωが0から∞まで変化すると、1から0まで変化します。

ハイパスフィルタ

名前が示すようにハイパスフィルターは、（パス）のみを許可します high frequencyコンポーネント。つまり、すべての低周波成分を拒否（ブロック）します。

sドメイン circuit diagram ハイパスフィルターの（ネットワーク）を下図に示します。

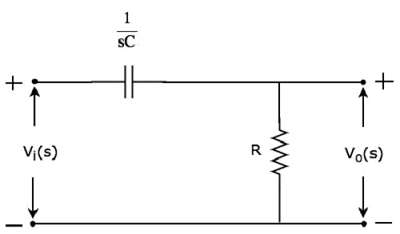
これは、2つの受動素子コンデンサと抵抗で構成されています。 series。入力電圧はこの組み合わせ全体に印加され、出力は抵抗器の両端の電圧と見なされます。

ここに、 $V_i(s)$ そして $V_o(s)$ 入力電圧のラプラス変換です。 $v_i(t)$ および出力電圧、 $v_o(t)$ それぞれ。

ザ・ transfer function 上記のネットワークの

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC}}$$

$$\Rightarrow H(s) = \frac{sCR}{1 + sCR}$$

代替、 $s = j \omega$ 上記の式で。

$$H(j \omega) = \frac{j \omega CR}{1 + j \omega CR}$$

伝達関数の大きさは

$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 + (\omega CR)^2}}$$

• でω = 0、伝達関数の大きさは0に等しいです。

• で $\omega = \frac{1}{CR}$、伝達関数の大きさは0.707に等しくなります。

• でω =∞、伝達関数の大きさは1に等しいです。

したがって、の伝達関数の大きさ High pass filter以下のように0から1に変化するであろうωが0から∞まで変化します。

バンドパスフィルター

名前が示すようにバンドパスフィルター、それ allows （合格）のみ one band周波数の。一般に、この周波数帯域は低周波数範囲と高周波数範囲の間にあります。つまり、このフィルターは低周波数成分と高周波数成分の両方を拒否（ブロック）します。

sドメイン circuit diagram バンドパスフィルターの（ネットワーク）を下図に示します。

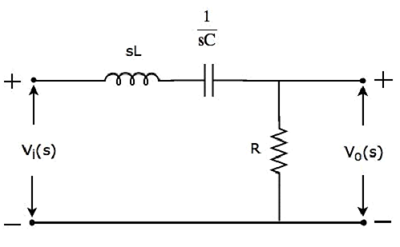
これは、インダクタ、コンデンサ、抵抗の3つの受動素子で構成されています。 series。入力電圧はこの組み合わせ全体に印加され、出力は抵抗器の両端の電圧と見なされます。

ここに、 $V_i(s)$ そして $V_o(s)$ 入力電圧のラプラス変換です。 $v_i(t)$ および出力電圧、 $v_o(t)$ それぞれ。

ザ・ transfer function 上記のネットワークの

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC} + sL}$$

$$\Rightarrow H(s) = \frac{s CR}{s^2 LC + sCR + 1}$$

代替 $s = j \omega$ 上記の式で。

$$H(j \omega) = \frac{j \omega CR}{1 - \omega^2 LC + j \omega CR}$$

伝達関数の大きさは

$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$

• でω = 0、伝達関数の大きさは0に等しいです。

• で $\omega = \frac{1}{\sqrt{LC}}$、伝達関数の大きさは1に等しい。

• でω =∞、伝達関数の大きさは0に等しいです。

したがって、の伝達関数の大きさ Band pass filterωが0から∞まで変化すると、0から1および1から0まで変化します。

バンドストップフィルター

名前が示すように、バンドストップフィルターは、周波数の1つの帯域のみを拒否（ブロック）します。一般に、この周波数帯域は低周波数範囲と高周波数範囲の間にあります。つまり、このフィルターは低周波数成分と高周波数成分の両方を許可（通過）します。

のsドメイン（ネットワーク） circuit diagramストップフィルターを次の図に示します。

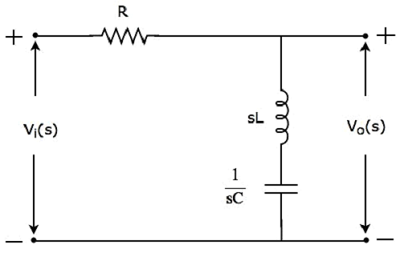
これは、抵抗、インダクタ、コンデンサの3つの受動素子で構成されています。 series。入力電圧はこの組み合わせ全体に印加され、出力はインダクタとコンデンサの組み合わせの両端の電圧と見なされます。

ここに、 $V_i(s)$ そして $V_o(s)$ 入力電圧のラプラス変換です。 $v_i(t)$ および出力電圧、 $v_o(t)$ それぞれ。

ザ・ transfer function 上記のネットワークの

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{sL + \frac{1}{sC}}{R + sL + \frac{1}{sC}}$$

$$\Rightarrow H(s) = \frac{s^2 LC + 1}{s^2 LC + sCR + 1}$$

代替、 $s = j \omega$ 上記の式で。

$$H(j \omega) = \frac{1 - \omega^2 LC}{1 - \omega^2 LC + j \omega CR}$$

伝達関数の大きさは

$$|H(j \omega)| = \frac{1 - \omega^2 LC}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$

• でω = 0、伝達関数の大きさは1に等しいです。

• で $\omega = \frac{1}{\sqrt{LC}}$、伝達関数の大きさは0に等しい。

• でω =∞、伝達関数の大きさは1に等しいです。

したがって、の伝達関数の大きさ Band stop filterωが0から∞まで変化すると、1から0および0から1まで変化します。