ネットワーク理論-AC回路の応答
前の章では、DC回路の過渡応答と定常応答について説明しました。この章では、response of AC circuit。前の章で説明した過渡応答と定常状態応答の両方の概念は、ここでも役立ちます。
シリーズRL回路の応答を見つける
次のことを考慮してください series RL circuit 図。

上記の回路では、 switch 保たれた openまで、T = 0とそれがで閉鎖されたT = 0。したがって、ピーク電圧がV mボルトのAC電圧源は、この時点まで直列RL回路に接続されていません。したがって、no initial current インダクタを流れます。
回路図、 switch にあります closed 位置は、次の図に示されています。
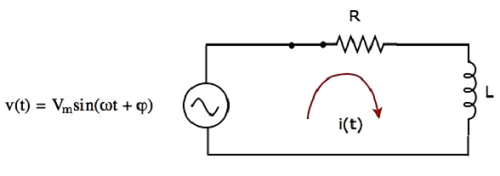
ここで、V mボルトのピーク電圧を持つAC電圧源が直列RL回路に接続されているため、電流i(t)が回路全体に流れます。
上記の回路を流れる電流i(t)には、過渡部分を表す項と定常状態を表す項の2つの項があることがわかっています。
数学的には、次のように表すことができます。
$ i(t)= i_ {Tr}(t)+ i_ {ss}(t)$Equation 1
どこ、
$ i_ {Tr}(t)$は、回路を流れる電流の過渡応答です。
$ i_ {ss}(t)$は、回路を流れる電流の定常状態応答です。
前の章では、直列RL回路を流れる電流の過渡応答を取得しました。$ Ke ^ {-\ lgroup \ frac {t} {\ tau} \ rgroup} $の形式です。
式1に$ i_ {Tr}(t)= Ke ^ {-\ lgroup \ frac {t} {\ tau} \ rgroup} $を代入します。
$ i(t)= Ke ^ {-\ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss}(t)$Equation 2
定常電流の計算
正弦波信号が線形電気回路への入力として適用されると、定常状態の出力が生成されます。これは、 sinusoidal signal。入力と出力の両方の正弦波信号は同じ周波数を持ちますが、振幅と位相角は異なります。
電気回路が正弦波電圧源によって励起されたときの定常状態応答は、次を使用して計算できます。 Laplace Transform approach。
sドメイン回路図、 switch にあります closed 位置は、次の図に示されています。
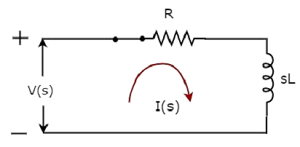
上記の回路では、すべての量とパラメータは次のように表されます。 s-domain。これらは、時間領域の量とパラメーターのラプラス変換です。
ザ・ Transfer function 上記の回路の
$$ H(s)= \ frac {I(s)} {V(s)} $$
$$ \ Rightarrow H(s)= \ frac {1} {Z(s)} $$
$$ \ Rightarrow H(s)= \ frac {1} {R + sL} $$
上記の式に$ s = j \ omega $を代入します。
$$ H(j \ omega)= \ frac {1} {R + j \ omega L} $$
Magnitude of $ \ mathbf {\ mathit {H(j \ omega)}} $は
$$ | H(j \ omega)| = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$
Phase angle of $ \ mathbf {\ mathit {H(j \ omega)}} $は
$$ \ angle H(j \ omega)= -tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$
取得します steady state current $ i_ {ss}(t)$次の2つの手順を実行します-
入力正弦波電圧のピーク電圧と$ H(j \ omega)$の大きさを乗算します。
入力正弦波電圧と$ H(j \ omega)$の位相角を追加します。
ザ・ steady state current $ i_ {ss}(t)$は
$$ i_ {ss}(t)= \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi --tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
式2の$ i_ {ss}(t)$の値を代入します。
$ i(t)= Ke ^ {-\ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi --tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 3
回路には初期電流がないことがわかっています。したがって、定数Kの値を見つけるには、式3にt = 0&i(t)= 0を代入します。
$$ 0 = Ke ^ {-\ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \オメガ(0)+ \ varphi --tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi --tan ^ {-1} \ lgroup \ frac {\オメガL} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow K =-\ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi --tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
式3にKの値を代入します。
$ i(t)=-\ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi --tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {-\ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi --tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 4
式4は、正弦波電圧源によって励起されたときに直列RL回路を流れる電流を表しています。それは2つの用語を持っています。第1項と第2項は、それぞれ電流の過渡応答と定常状態応答を表します。
私たちはできる neglect the first termその値は1より非常に小さいため、式4の したがって、回路を流れる結果として生じる電流は次のようになります。
$$ i(t)= \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi --tan ^ {-1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
のみが含まれています steady state term。したがって、AC回路の定常応答のみを見つけ、その過渡応答を無視することができます。