ネットワーク理論-受動素子
この章では、抵抗、インダクタ、コンデンサなどの受動素子について詳しく説明します。抵抗器から始めましょう。
抵抗器
抵抗器の主な機能は、電流の流れに対抗するか制限することです。したがって、抵抗は、電流の量および/または分割(共有)電圧を制限するために使用されます。
抵抗器を流れる電流を1アンペア、両端の電圧をVボルトとします。ザ・symbol 次の図に、抵抗器と電流Iおよび電圧Vを示します。
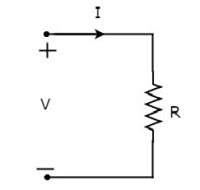
による Ohm’s law、抵抗器の両端の電圧は、抵抗器を流れる電流とその抵抗器の抵抗の積です。 Mathematically、次のように表すことができます
$ V = IR $ Equation 1
$ \ Rightarrow I = \ frac {V} {R} $Equation 2
どこ、 R は抵抗器の抵抗です。
式2から、抵抗を流れる電流は抵抗の両端に印加される電圧に正比例し、抵抗の抵抗に反比例すると結論付けることができます。
Power 電気回路要素では、次のように表すことができます
$ P = VI $Equation 3
式3の式1を代入します。
$ P =(IR)I $
$ \ Rightarrow P = I ^ 2 R $ Equation 4
式3の式2を代入します。
$ P = V \ lgroup \ frac {V} {R} \ rgroup $
$ \ Rightarrow P = \ frac {V ^ 2} {R} $ Equation 5
したがって、式3〜5に記載されている式のいずれかを使用して、抵抗で消費される電力量を計算できます。
インダクタ
一般に、インダクタには巻数があります。したがって、電流が流れると磁束が発生します。したがって、インダクタによって生成される総磁束の量は電流に依存し、私はインダクタを流れ、それらは線形関係にあります。
Mathematically、次のように書くことができます
$$ \ Psi \:\ alpha \:I $$
$$ \ Rightarrow \ Psi = LI $$
どこ、
Ψ は総磁束です
L インダクタのインダクタンスです
インダクタを流れる電流を1アンペア、両端の電圧をVボルトとします。ザ・symbol次の図に、インダクタの電流Iと電圧Vを示します。
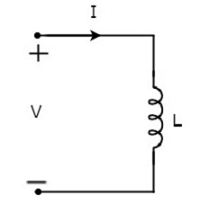
による Faraday’s law、インダクタ両端の電圧は次のように書くことができます。
$$ V = \ frac {d \ Psi} {dt} $$
置換Ψ= LIを上記式に。
$$ V = \ frac {d(LI)} {dt} $$
$$ \ Rightarrow V = L \ frac {dI} {dt} $$
$$ \ Rightarrow I = \ frac {1} {L} \ int V dt $$
上記の式から、次の式が存在すると結論付けることができます。 linear relationship インダクタ両端の電圧とインダクタを流れる電流の間。
私達はことを知っています power 電気回路要素では、次のように表すことができます
$$ P = VI $$
上記の式に$ V = L \ frac {dI} {dt} $を代入します。
$$ P = \ lgroup L \ frac {dI} {dt} \ rgroup I $$
$$ \ Rightarrow P = LI \ frac {dI} {dt} $$
上記の式を積分することにより、次の式が得られます。 energy としてインダクタに格納されます
$$ W = \ frac {1} {2} LI ^ 2 $$
したがって、インダクタはエネルギーを磁場の形で蓄積します。
コンデンサ
一般に、コンデンサには、誘電体媒体によって分離された2つの導電性プレートがあります。コンデンサの両端に正の電圧が印加されると、正の電荷が蓄積されます。同様に、コンデンサの両端に負の電圧が印加されると、負の電荷が蓄積されます。
したがって、コンデンサに蓄積される電荷の量は、印加電圧に依存します Vそれを横切って、彼らは線形関係を持っています。数学的には、次のように書くことができます
$$ Q \:\ alpha \:V $$
$$ \ Rightarrow Q = CV $$
どこ、
Q はコンデンサに蓄積された電荷です。
C はコンデンサの静電容量です。
コンデンサを流れる電流を1アンペア、両端の電圧をVボルトとします。次の図に、コンデンサの記号と電流Iおよび電圧Vを示します。
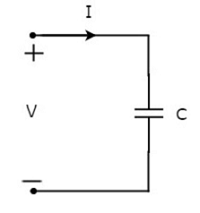
私たちは、 current に他なりません time rate of flow of charge。数学的には、次のように表すことができます。
$$ I = \ frac {dQ} {dt} $$
上記の式に$ Q = CV $を代入します。
$$ I = \ frac {d(CV)} {dt} $$
$$ \ Rightarrow I = C \ frac {dV} {dt} $$
$$ \ Rightarrow V = \ frac {1} {C} \ int I dt $$
上記の式から、次の式が存在すると結論付けることができます。 linear relationship コンデンサ両端の電圧とコンデンサを流れる電流の間。
私達はことを知っています power 電気回路要素では、次のように表すことができます
$$ P = VI $$
上記の式に$ I = C \ frac {dV} {dt} $を代入します。
$$ P = V \ lgroup C \ frac {dV} {dt} \ rgroup $$
$$ \ Rightarrow P = CV \ frac {dV} {dt} $$
上記の式を積分することにより、次の式が得られます。 energy としてコンデンサに格納されます
$$ W = \ frac {1} {2} CV ^ 2 $$
したがって、コンデンサは電界の形でエネルギーを蓄えます。