디지털 신호 처리-기본 CT 신호
시스템을 테스트하기 위해 일반적으로 표준 또는 기본 신호가 사용됩니다. 이러한 신호는 많은 복잡한 신호의 기본 구성 요소입니다. 따라서 신호 및 시스템 연구에서 매우 중요한 역할을합니다.
단위 임펄스 또는 델타 함수
조건 $ \ delta (t) = \ lim _ {\ epsilon \ to \ infty} x (t) $를 만족하는 신호를 단위 임펄스 신호라고합니다. 이 신호는 t = 0 일 때 무한대가되고 t ≠ 0 일 때 0이되는 경향이있어 곡선 아래의 면적이 항상 1과 같습니다. 델타 함수는 t = 0에서 excunit_impulse.jpgept 모든 곳에서 진폭이 0입니다.

단위 임펄스 신호의 속성
- δ (t)는 짝수 신호입니다.
- δ (t)는 에너지도 전력 (NENP) 신호도 아닌 예입니다.
- 단위 임펄스 신호의 영역은 다음과 같이 쓸 수 있습니다. $$ A = \ int _ {-\ infty} ^ {\ infty} \ delta (t) dt = \ int _ {-\ infty} ^ {\ infty} \ lim _ {\ epsilon \ to 0} x (t) dt = \ lim _ {\ epsilon \ to 0} \ int _ {-\ infty} ^ {\ infty} [x (t) dt] = 1 $$
- 신호의 무게 또는 강도는 다음과 같이 쓸 수 있습니다. $$ y (t) = A \ 델타 (t) $$
- 가중 된 임펄스 신호의 영역은 다음과 같이 쓸 수 있습니다. $$ y (t) = \ int _ {-\ infty} ^ {\ infty} y (t) dt = \ int _ {-\ infty} ^ {\ infty} A \ delta (t) = A [\ int _ {- \ infty} ^ {\ infty} \ delta (t) dt] = A = 1 = Wigthedimpulse $$
단위 단계 신호
다음 두 조건을 만족하는 신호-
- $ U (t) = 1 (when \ quad t \ geq 0) 및 $
- $ U (t) = 0 (\ quad t <0) $
단위 단계 신호라고합니다.
t = 0에서 불연속성을 나타내는 속성을 가지고 있습니다. 불연속 점에서 신호 값은 신호 값의 평균으로 주어집니다. 이 신호는 불연속 지점 (Gib 's Phenomena에 따르면) 직전과 직후에 취해졌습니다.
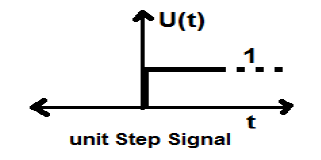
시간 스케일링 된 다른 단계 신호에 단계 신호를 추가하면 결과는 단일성이됩니다. 전력 형 신호이며 전력 값은 0.5입니다. RMS (루트 평균 제곱) 값은 0.707이고 평균 값도 0.5입니다.
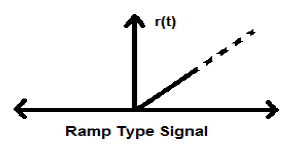
램프 신호
단계 신호를 통합하면 램프 신호가 생성됩니다. r (t)로 표시됩니다. 램프 신호는 $ r (t) = \ int _ {-\ infty} ^ {t} U (t) dt = tU (t) $ 조건도 충족합니다. 에너지도 전력 (NENP) 유형 신호도 아닙니다.
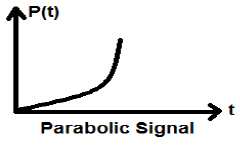
포물선 신호
램프 신호의 통합은 포물선 신호로 이어집니다. p (t)로 표시됩니다. 포물선 신호는 조건 $ p (t) = \ int _ {-\ infty} ^ {t} r (t) dt = (t ^ {2} / 2) U (t) $를 충족합니다. 에너지도 전력 (NENP) 유형 신호도 아닙니다.
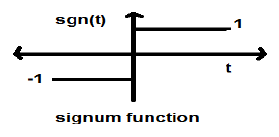
Signum 기능
이 기능은 다음과 같이 표현됩니다.
$$ sgn (t) = \ begin {cases} 1 & for \ quad t> 0 \\-1 & for \ quad t <0 \ end {cases} $$파워 타입 신호입니다. 전력 값과 RMS (Root mean square) 값은 모두 1입니다. signum 함수의 평균 값은 0입니다.
Sinc 기능
또한 사인의 함수이며 다음과 같이 작성됩니다.
$$ SinC (t) = \ frac {Sin \ Pi t} {\ Pi T} = Sa (\ Pi t) $$Sinc 함수의 특성
에너지 유형 신호입니다.
$ Sinc (0) = \ lim_ {t \ to 0} \ frac {\ sin \ Pi t} {\ Pi t} = 1 $
$ Sinc (\ infty) = \ lim_ {t \ to \ infty} \ frac {\ sin \ Pi \ infty} {\ Pi \ infty} = 0 $ (sinπ∞의 범위는 -1에서 +1까지 다양하지만 나누어 진 것은 무한대로 0과 같음)
-
$ \ sin c (t) = 0 => \ sin \ Pi t = 0 $ 인 경우
$ \ Rightarrow \ Pi t = n \ Pi $
$ \ 오른쪽 화살표 t = n (n \ neq 0) $
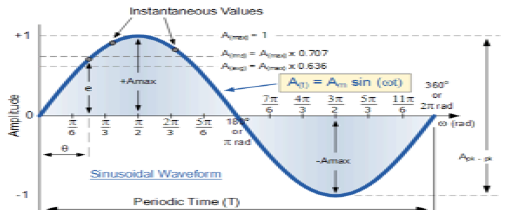
정현파 신호
본질적으로 연속적인 신호를 연속 신호라고합니다. 정현파 신호의 일반적인 형식은 다음과 같습니다.
$$ x (t) = A \ sin (\ omega t + \ phi) $$여기,
A = 신호의 진폭
ω = 신호의 각 주파수 (라디안으로 측정)
φ = 신호의 위상 각 (라디안으로 측정)
이 신호는 일정 시간이 지나면 반복되는 경향이 있으므로 주기적 신호라고합니다. 신호의 기간은 다음과 같습니다.
$$ T = \ frac {2 \ pi} {\ omega} $$정현파 신호의 다이어그램보기는 다음과 같습니다.
직사각형 기능
신호가 다음 조건을 충족하면 직사각형 함수 유형이라고합니다.
$$ \ pi (\ frac {t} {\ tau}) = \ begin {cases} 1, for \ quad t \ leq \ frac {\ tau} {2} \\ 0, 그렇지 않으면 \ end {cases} $$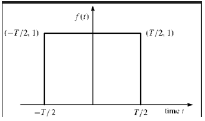
Y 축에 대해 대칭이기 때문에이 신호를 짝수 신호라고합니다.
삼각 펄스 신호
다음 조건을 충족하는 모든 신호를 삼각 신호라고합니다.
$$ \ Delta (\ frac {t} {\ tau}) = \ begin {cases} 1-(\ frac {2 | t |} {\ tau}) & for | t | <\ frac {\ tau} { 2} \\ 0 및 for | t |> \ frac {\ tau} {2} \ end {cases} $$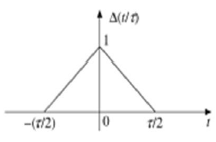
이 신호는 Y 축에 대해 대칭입니다. 따라서 짝수 신호라고도합니다.