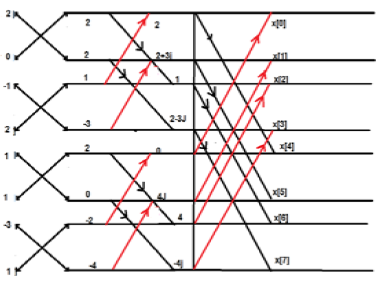
DSP-고속 푸리에 변환
이전 DFT 방법에서는 계산 부분이 너무 깁니다. 우리는 그것을 줄이고 싶습니다. 이는 FFT 또는 고속 푸리에 변환을 통해 수행 할 수 있습니다. 따라서 FFT는 계산 부분이 감소되는 알고리즘 형식의 이산 푸리에 변환 계산에 불과하다고 말할 수 있습니다.
FFT를 사용하는 가장 큰 장점은 FFT를 통해 FIR 필터를 설계 할 수 있다는 것입니다. 수학적으로 FFT는 다음과 같이 작성할 수 있습니다.
$$ x [K] = \ displaystyle \ sum \ limits_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$더 잘 이해하기 위해 예를 들어 보겠습니다. $ x_0 \ quad에서 \ quad x_7 $까지 이름이 지정된 8 개의 포인트를 고려했습니다. 한 그룹에서는 짝수 항을 선택하고 다른 그룹에서는 홀수 항을 선택합니다. 위의 다이어그램보기는 아래에 나와 있습니다.
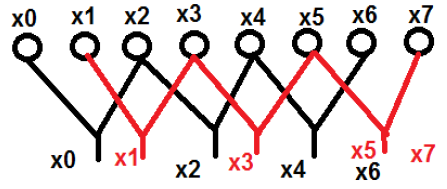
여기서 포인트 x 0 , x 2 , x 4 및 x 6 은 하나의 범주로 그룹화되었으며 유사하게 x 1 , x 3 , x 5 및 x 7 점이 다른 범주에 포함되었습니다. 이제 우리는 그것들을 두 그룹으로 더 만들고 계산을 진행할 수 있습니다. 이제이 두 개로 나뉘어 계산이 어떻게 도움이되는지 살펴 보겠습니다.
$ x [k] = \ displaystyle \ sum \ limits_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limits_ {r = 0 } ^ {\ frac {N} {2} -1} x [2r + 1] W_N ^ {(2r + 1) k} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ times W_N ^ k $
$ = G [k] + H [k] \ times W_N ^ k $
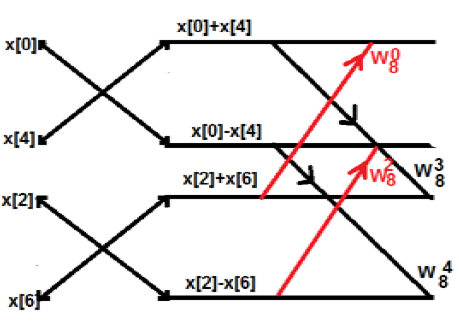
처음에는 8 점 시퀀스를 사용했지만 나중에이 시퀀스를 G [k]와 H [k] 두 부분으로 분리했습니다. G [k]는 짝수 부분을 나타내고 H [k]는 홀수 부분을 나타냅니다. 다이어그램을 통해 실현하고 싶다면 다음과 같이 나타낼 수 있습니다.
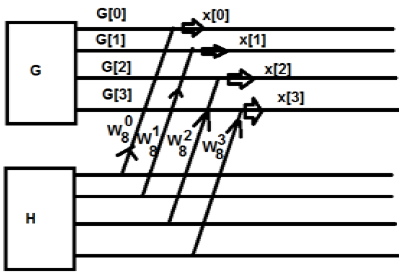
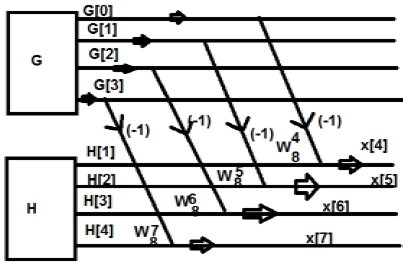
위 그림에서 우리는
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
마찬가지로 최종 값은 다음과 같이 쓸 수 있습니다.
$ G [0] ~ H [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
위의 것은 주기적 시리즈입니다. 이 시스템의 단점은 K가 4 점 이상으로 깨질 수 없다는 것입니다. 이제 위의 내용을 더 자세히 살펴 보겠습니다. 우리는 다음과 같은 구조를 얻을 것입니다.
예
x [n] = {2,1, -1, -3,0,1,2,1} 시퀀스를 고려하십시오. FFT를 계산합니다.
Solution − 주어진 시퀀스는 x [n] = {2,1, -1, -3,0,1,2,1}입니다.
아래와 같이 용어를 정렬하십시오.