DSP-신호 통합 작업
모든 신호의 통합은 수정 된 신호를 얻기 위해 특정 시간 도메인에서 해당 신호의 합계를 의미합니다. 수학적으로 이것은 다음과 같이 나타낼 수 있습니다.
$$ x (t) \ rightarrow y (t) = \ int _ {-\ infty} ^ {t} x (t) dt $$여기에서도 대부분의 경우 수학적 통합을 수행하고 결과 신호를 찾을 수 있지만 직사각형 형식으로 그래픽으로 표시된 신호에 대해 빠른 연속 직접 통합이 가능합니다. 미분과 마찬가지로 여기에서도 결과를 빠르게 얻기 위해 표를 참조합니다.
| 원래 신호 | 통합 신호 |
|---|---|
| 1 | 충동 |
| 충동 | 단계 |
| 단계 | 비탈길 |
예
$ x (t) = u (t) -u (t-3) $ 신호를 생각해 봅시다. 아래 그림 -1에 나와 있습니다. 분명히 우리는 그것이 단계 신호라는 것을 알 수 있습니다. 이제 우리는 그것을 통합 할 것입니다. 표를 참조하면 단계 신호의 통합이 램프 신호를 생성한다는 것을 알고 있습니다.
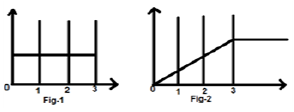
그러나 우리는 그것을 수학적으로 계산할 것입니다.
$ y (t) = \ int _ {-\ infty} ^ {t} x (t) dt $
$ = \ int _ {-\ infty} ^ {t} [u (t) -u (t-3)] dt $
$ = \ int _ {-\ infty} ^ {t} u (t) dt- \ int _ {-\ infty} ^ {t} u (t-3) dt $
$ = r (t) -r (t-3) $
그림 2와 같이 동일하게 표시됩니다.