DSP-Z- 변환 속성
이 장에서는 Z 변환의 기본 속성을 이해합니다.
선형성
두 개 이상의 개별 이산 신호에 상수를 곱하면 해당 Z 변환도 동일한 상수로 곱해집니다.
수학적으로
$$ a_1x_1 (n) + a_2x_2 (n) = a_1X_1 (z) + a_2X_2 (z) $$Proof − 우리는 알고 있습니다.
$$ X (Z) = \ sum_ {n =-\ infty} ^ \ infty x (n) Z ^ {-n} $$$ = \ sum_ {n =-\ infty} ^ \ infty (a_1x_1 (n) + a_2x_2 (n)) Z ^ {-n} $
$ = a_1 \ sum_ {n =-\ infty} ^ \ infty x_1 (n) Z ^ {-n} + a_2 \ sum_ {n =-\ infty} ^ \ infty x_2 (n) Z ^ {-n} $
$ = a_1X_1 (z) + a_2X_2 (z) $ (따라서 입증 됨)
여기서 ROC는 $ ROC_1 \ bigcap ROC_2 $입니다.
시간 이동
시간 이동 속성은 이산 신호에서 시간 도메인의 변화가 Z 도메인에 어떻게 영향을 미치는지 보여줍니다.
$$ x (n-n_0) \ longleftrightarrow X (Z) Z ^ {-n} $$또는 $ x (n-1) \ longleftrightarrow Z ^ {-1} X (Z) $
Proof −
하자 $ Y (P) = X (PK)을 $
$ Y (z) = \ sum_ {p =-\ infty} ^ \ infty y (p) Z ^ {-p} $
$ = \ sum_ {p =-\ infty} ^ \ infty (x (pk)) Z ^ {-p} $
s = pk
$ = \ sum_ {s =-\ infty} ^ \ infty x (s) Z ^ {-(s + k)} $
$ = \ sum_ {s =-\ infty} ^ \ infty x (s) Z ^ {-s} Z ^ {-k} $
$ = Z ^ {-k} [\ sum_ {s =-\ infty} ^ \ infty x (m) Z ^ {-s}] $
$ = Z ^ {-k} X (Z) $ (따라서 입증 됨)
여기서 ROC는 Z = 0 (p> 0) 또는 Z = ∞ (p <0)로 쓸 수 있습니다.
예
U (n) 및 U (n-1)은 다음과 같이 플로팅 할 수 있습니다.
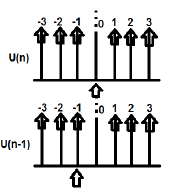
U (n) cab의 Z 변환은 다음과 같이 작성됩니다.
$ \ sum_ {n =-\ infty} ^ \ infty [U (n)] Z ^ {-n} = 1 $
U (n-1)의 Z 변환은 다음과 같이 쓸 수 있습니다.
$ \ sum_ {n =-\ infty} ^ \ infty [U (n-1)] Z ^ {-n} = Z ^ {-1} $
그래서 여기 $ x (n-n_0) = Z ^ {-n_0} X (Z) $ (따라서 입증 됨)
시간 척도
Time Scaling 속성은 시간이 불연속적인 형태로 스케일 될 때 신호의 Z 영역이 무엇인지 알려줍니다. 다음과 같이 쓸 수 있습니다.
$$ a ^ nx (n) \ longleftrightarrow X (a ^ {-1} Z) $$Proof −
하자 $ Y (p) = A ^ {P} × (P)을 $
$ Y (P) = \ sum_ {p =-\ infty} ^ \ infty y (p) Z ^ {-p} $
$ = \ sum_ {p =-\ infty} ^ \ infty a ^ px (p) Z ^ {-p} $
$ = \ sum_ {p =-\ infty} ^ \ infty x (p) [a ^ {-1} Z] ^ {-p} $
$ = X (a ^ {-1} Z) $ (따라서 입증 됨)
ROC : = Mod (ar1) <Mod (Z) <Mod (ar2) 여기서 Mod = Modulus
예
시간 스케일링 속성을 사용하여 $ x (n) = a ^ n \ cos \ omega n $의 Z 변환을 결정하겠습니다.
Solution −
우리는 이미 $ \ cos (\ omega n) $ 신호의 Z- 변환이-
$$ \ sum_ {n =-\ infty} ^ \ infty (\ cos \ omega n) Z ^ {-n} = (Z ^ 2-Z \ cos \ omega) / (Z ^ 2-2Z \ cos \ omega +1) $$
이제 시간 스케일링 속성을 적용하여 $ a ^ n \ cos \ omega n $의 Z 변환을 다음과 같이 작성할 수 있습니다.
$ \ sum_ {n =-\ infty} ^ \ infty (a ^ n \ cos \ omega n) Z ^ {-n} = X (a ^ {-1} Z) $
$ = [(a ^ {-1} Z) ^ 2- (a ^ {-1} Z \ cos \ omega n)] / ((a ^ {-1} Z) ^ 2-2 (a ^ {- 1} Z \ cos \ omega n) +1) $
$ = Z (Za \ cos \ omega) / (Z ^ 2-2az \ cos \ omega + a ^ 2) $
연속적인 차별화
연속적인 미분 속성은 시간과 관련하여 시간 도메인에서 이산 신호를 미분 할 때 Z 변환이 발생 함을 보여줍니다. 다음과 같이 표시됩니다.
$$ \ frac {dx (n)} {dn} = (1-Z ^ {-1}) X (Z) $$Proof −
방정식의 LHS를 고려하십시오 − $ \ frac {dx (n)} {dn} $
$$ = \ frac {[x (n) -x (n-1)]} {[n- (n-1)]} $$$ = x (n) -X (n-1) $
$ = x (Z) -Z ^ {-1} x (Z) $
$ = (1-Z ^ {-1}) x (Z) $ (따라서 입증 됨)
ROC : R1 <Mod (Z) <R2
예
$ x (n) = n ^ 2u (n) $에 의해 주어진 신호의 Z 변환을 찾아 봅시다.
속성으로 우리는 쓸 수 있습니다
$ Zz [nU (n)] = -Z \ frac {dZ [U (n)]} {dz} $
$ = -Z \ frac {d [\ frac {Z} {Z-1}]} {dZ} $
$ = Z / ((Z-1) ^ 2 $
$ = y (렛) $
이제 속성을 다시 적용하여 Z [ny]를 찾을 수 있습니다.
$ Z (n, y) = -Z \ frac {dy} {dz} $
$ = -Z \ frac {d [Z / (Z-1) ^ 3]} {dz} $
$ = Z (Z + 1) / (Z-1) ^ 2 $
회선
이것은 컨볼 루션이 이산 신호 형태로 발생할 때 시스템의 Z 영역의 변화를 묘사하며 다음과 같이 쓸 수 있습니다.
$ x_1 (n) * x_2 (n) \ longleftrightarrow X_1 (Z) .X_2 (Z) $
Proof −
$ X (Z) = \ sum_ {n =-\ infty} ^ \ infty x (n) Z ^ {-n} $
$ = \ sum_ {n =-\ infty} ^ \ infty [\ sum_ {k =-\ infty} ^ \ infty x_1 (k) x_2 (nk)] Z ^ {-n} $
$ = \ sum_ {k =-\ infty} ^ \ infty x_1 (k) [\ sum_n ^ \ infty x_2 (nk) Z ^ {-n}] $
$ = \ sum_ {k =-\ infty} ^ \ infty x_1 (k) [\ sum_ {n =-\ infty} ^ \ infty x_2 (nk) Z ^ {-(nk)} Z ^ {-k}] $
nk = l, 위의 방정식 cab은 다음과 같이 작성됩니다.
$ X (Z) = \ sum_ {k =-\ infty} ^ \ infty x_1 (k) [Z ^ {-k} \ sum_ {l =-\ infty} ^ \ infty x_2 (l) Z ^ {-l }] $
$ = \ sum_ {k =-\ infty} ^ \ infty x_1 (k) X_2 (Z) Z ^ {-k} $
$ = X_2 (Z) \ sum_ {k =-\ infty} ^ \ infty x_1 (Z) Z ^ {-k} $
$ = X_1 (Z) .X_2 (Z) $ (따라서 입증 됨)
ROC : $ ROC \ bigcap ROC2 $
예
두 신호에 의해 주어진 컨볼 루션을 찾아 보자
$ x_1 (n) = \ lbrace 3, -2,2 \ rbrace $ ... ( 등식 1)
$ x_2 (n) = \ lbrace 2,0 \ leq 4 \ quad 및 \ quad 0 \ quad 다른 곳 \ rbrace $ ... (eq. 2)
첫 번째 방정식의 Z 변환은 다음과 같이 쓸 수 있습니다.
$ \ sum_ {n =-\ infty} ^ \ infty x_1 (n) Z ^ {-n} $
$ = 3-2Z ^ {-1} + 2Z ^ {-2} $
두 번째 신호의 Z- 변환은 다음과 같이 쓸 수 있습니다.
$ \ sum_ {n =-\ infty} ^ \ infty x_2 (n) Z ^ {-n} $
$ = 2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4} $
따라서 위 두 신호의 컨볼 루션은 다음과 같습니다.
$ X (Z) = [x_1 (Z) ^ * x_2 (Z)] $
$ = [3-2Z ^ {-1} + 2Z ^ {-2}] \ times [2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4 }] $
$ = 6 + 2Z ^ {-1} + 6Z ^ {-2} + 6Z ^ {-3} + ... \ quad ... \ quad ... $
역 Z- 변환을 취하면
$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $
초기 값 정리
x (n)이 Z 변환이 X (z) 인 인과 시퀀스이면 초기 값 정리는 다음과 같이 쓸 수 있습니다.
$ X (n) (at \ quad n = 0) = \ lim_ {z \ to \ infty} X (z) $
Proof − 우리는 알고 있습니다.
$ X (Z) = \ sum_ {n = 0} ^ \ infty x (n) Z ^ {-n} $
위의 시리즈를 확장하면 다음과 같습니다.
$ = X (0) Z ^ 0 + X (1) Z ^ {-1} + X (2) Z ^ {-2} + ... \ quad ... $
$ = X (0) \ times 1 + X (1) Z ^ {-1} + X (2) Z ^ {-2} + ... \ quad ... $
위의 경우 Z → ∞이면 $ Z ^ {-n} \ rightarrow 0 $ (n> 0이기 때문에)
따라서 우리는 말할 수 있습니다.
$ \ lim_ {z \ to \ infty} X (z) = X (0) $ (따라서 입증 됨)
최종 가치 정리
최종 값 정리에 따르면 신호의 Z 변환이 X (Z)로 표시되고 극점이 모두 원 안에 있으면 최종 값은 x (n) 또는 X (∞)로 표시되며 다음과 같이 쓸 수 있습니다. −
$ X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {-1})] $
Conditions −
- 인과 시스템에만 적용됩니다.
- $ X (Z) (1-Z ^ {-1}) $에는 Z 평면의 단위 원 안에 극이 있어야합니다.
Proof − 우리는
$ Z ^ + [x (n + 1) -x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x (n + 1) -x (n)] $
$ \ 오른쪽 화살표 Z ^ + [x (n + 1)]-Z ^ + [x (n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x (n + 1) -x (n)] $
$ \ 오른쪽 화살표 Z [X (Z) ^ +-x (0)]-X (Z) ^ + = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x (n + 1) -x (n)] $
여기서 우리는 단측 Z- 변환의 고급 속성을 적용 할 수 있습니다. 따라서 위의 방정식은 다음과 같이 다시 작성할 수 있습니다.
$ Z ^ + [x (n + 1)] = Z [X (2) ^ +-x (0) Z ^ 0] = Z [X (Z) ^ +-x (0)] $
이제 위 방정식에 z = 1을 입력하면 위 방정식을 확장 할 수 있습니다.
$ \ lim_ {k \ to \ infty} {[x (1) -x (0) + x (6) -x (1) + x (3) -x (2) + ... \ quad ... \ quad ... + x (x + 1) -x (k)]} $
이것은 다음과 같이 공식화 될 수 있습니다.
$ X (\ infty) = \ lim_ {n \ to \ infty} X (n) = \ lim_ {z \ to 1} [X (Z) (1-Z ^ {-1})] $ (따라서 입증 됨)
예
신호가 다음과 같이 주어진 x (n)의 초기 값과 최종 값을 찾아 봅시다.
$ X (Z) = 2 + 3Z ^ {-1} + 4Z ^ {-2} $
Solution − 먼저 정리를 적용하여 신호의 초기 값을 찾아 보겠습니다.
$ x (0) = \ lim_ {z \ to \ infty} X (Z) $
$ = \ lim_ {z \ to \ infty} [2 + 3Z ^ {-1} + 4Z ^ {-2}] $
$ = 2 + (\ frac {3} {\ infty}) + (\ frac {4} {\ infty}) = 2 $
이제 정리를 적용한 신호의 최종 값을 찾으십시오.
$ x (\ infty) = \ lim_ {z \ to \ infty} [(1-Z ^ {-1}) X (Z)] $
$ = \ lim_ {z \ to \ infty} [(1-Z ^ {-1}) (2 + 3Z ^ {-1} + 4Z ^ {-2})] $
$ = \ lim_ {z \ to \ infty} [2 + Z ^ {-1} + Z ^ {-2} -4Z ^ {-3}] $
$ = 2 + 1 + 1-4 = 0 $
Some other properties of Z-transform are listed below −
주파수의 차별화
이산 신호가 시간에 따라 미분 될 때 신호의 Z 도메인 변화를 제공합니다.
$ nx (n) \ longleftrightarrow -Z \ frac {dX (z)} {dz} $
ROC는 다음과 같이 작성할 수 있습니다.
$ r_2 <Mod (Z) <r_1 $
예
주파수 미분을 통해 x (n)의 값을 구해 보겠습니다. Z 도메인의 이산 신호는 $ x (n) \ longleftrightarrow X (Z) = log (1 + aZ ^ {-1}) $로 주어집니다.
속성별로 다음과 같이 작성할 수 있습니다.
$ nx (n) \ longleftrightarrow -Z \ frac {dx (Z)} {dz} $
$ = -Z [\ frac {-aZ ^ {-2}} {1 + aZ ^ {-1}}] $
$ = (aZ ^ {-1}) / (1 + aZ ^ {-1}) $
$ = 1-1 / (1 + aZ ^ {-1}) $
$ nx (n) = \ delta (n)-(-a) ^ nu (n) $
$ \ 오른쪽 화살표 x (n) = 1 / n [\ delta (n)-(-a) ^ nu (n)] $
시간의 곱셈
이산 신호 레벨에서 곱셈이 발생할 때 신호의 Z 도메인 변화를 제공합니다.
$ x_1 (n) .x_2 (n) \ longleftrightarrow (\ frac {1} {2 \ Pi j}) [X1 (Z) * X2 (Z)] $
시간 활용
이것은 Z- 도메인에서 공액 된 이산 신호의 표현을 묘사합니다.
$ X ^ * (n) \ longleftrightarrow X ^ * (Z ^ *) $