DSP-CT 신호 분류
연속 시간 신호는 신호에 대해 수행되는 여러 조건 또는 작업에 따라 분류 될 수 있습니다.
짝수 및 홀수 신호
짝수 신호
신호는 다음 조건을 만족해도된다고합니다.
$$ x (-t) = x (t) $$신호의 시간 반전은 여기에서 진폭의 변화를 의미하지 않습니다. 예를 들어 아래에 표시된 삼각파를 고려하십시오.
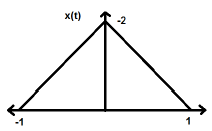
삼각 신호는 짝수 신호입니다. 따라서 Y 축에 대해 대칭입니다. Y 축에 대한 거울상이라고 할 수 있습니다.
아래 그림과 같이 다른 신호를 고려하십시오.
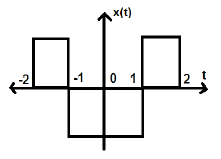
위의 신호가 Y 축에 대해 대칭 인 것을 알 수 있습니다.
이상한 신호
다음 조건을 충족하는 신호는 홀수라고합니다.
$$ x (-t) = -x (t) $$여기서 시간 반전과 진폭 변경이 동시에 발생합니다.
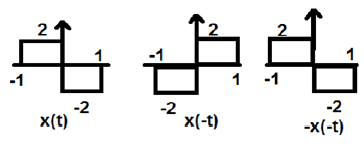
위 그림에서 단계 신호 x (t)를 볼 수 있습니다. 그것이 홀수 신호인지 아닌지를 테스트하기 위해 먼저 시간 반전 즉 x (-t)를 수행하고 그 결과는 그림과 같습니다. 그런 다음 결과 신호의 진폭, 즉 –x (-t)를 반전하고 그림과 같이 결과를 얻습니다.
첫 번째와 세 번째 파형을 비교해 보면 두 파형이 동일하다는 것을 알 수 있습니다. 즉, x (t) = -x (-t)가 기준을 충족합니다. 따라서 위의 신호는 Odd 신호입니다.
짝수 및 홀수 신호와 관련된 몇 가지 중요한 결과가 아래에 나와 있습니다.
- 짝수 × 짝수 = 짝수
- 홀수 × 홀수 = 짝수
- 짝수 × 홀수 = 홀수
- 짝수 ± 짝수 = 짝수
- 홀수 ± 홀수 = 홀수
- 짝수 ± 홀수 = 짝수도 홀수도 아님
모든 신호를 짝수 또는 홀수 형태로 표현
일부 신호는 짝수 또는 홀수 유형으로 직접 분류 할 수 없습니다. 이들은 짝수 및 홀수 신호의 조합으로 표시됩니다.
$$ x (t) \ rightarrow x_ {e} (t) + x_ {0} (t) $$여기서 x e (t)는 짝수 신호를 나타내고 x o (t)는 홀수 신호를 나타냅니다.
$$ x_ {e} (t) = \ frac {[x (t) + x (-t)]} {2} $$과
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$예
신호에서 짝수와 홀수 부분 찾기 $ x (n) = t + t ^ {2} + t ^ {3} $
Solution − x (n)을 반대로하면
$$ x (-n) = -t + t ^ {2} -t ^ {3} $$
이제 공식에 따르면 짝수 부분은
$$ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) + (-t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t ^ {2} $$
마찬가지로 공식에 따르면 홀수 부분은
$$ x_ {0} (t) = \ frac {[x (t) -x (-t)]} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3})-(-t + t ^ {2} -t ^ {3})]} {2} $$
$$ = t + t ^ {3} $$
주기적 및 비 주기적 신호
주기적 신호
주기적 신호는 일정한 시간 간격이 지나면 자체적으로 반복됩니다. 우리는 이것을 방정식 형태로 다음과 같이 보여줄 수 있습니다.
$$ x (t) = x (t) \ pm nT $$여기서 n = 정수 (1,2,3 ……)
T = 기본 기간 (FTP) ≠ 0 및 ≠ ∞
기본 기간 (FTP)은 신호가주기적인 가장 작은 양의 고정 시간 값입니다.
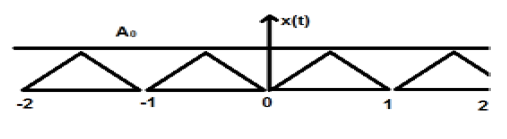
진폭 A의 위 그림에는 삼각형 신호가 표시되어 있습니다. 여기서 신호는 1 초마다 반복됩니다. 따라서 신호는 주기적이며 FTP는 1 초라고 말할 수 있습니다.
비 주기적 신호
간단히 말해 주기적이지 않은 신호는 본질적으로 비 주기적이라고 말할 수 있습니다. 당연히 이러한 신호는 간격 시간이 지나면 반복되지 않습니다.
비 주기적 신호는 특정 형식을 따르지 않습니다. 따라서 특별한 수학적 방정식이이를 설명 할 수 없습니다.
에너지 및 전력 신호
포함 된 총 에너지가 유한하고 0이 아닌 경우 (0 <E <∞) 인 경우에만 신호를 에너지 신호라고합니다. 따라서 모든 에너지 유형 신호의 경우 총 정규화 된 신호는 유한하고 0이 아닙니다.
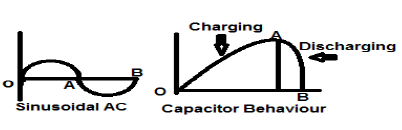
정현파 AC 전류 신호는 에너지 유형 신호의 완벽한 예입니다. 한 경우에는 양의 반주기에 있고 다음 반주기에는 음의 신호이기 때문입니다. 따라서 평균 전력은 0이됩니다.
무손실 커패시터는 또한 에너지 유형 신호의 완벽한 예입니다. 소스에 연결하면 최적 레벨까지 충전되고 소스가 제거되면 부하를 통해 동일한 양의 에너지를 소산하고 평균 전력을 제로.
유한 신호 x (t)에 대해 에너지는 E로 기호화 될 수 있으며 다음과 같이 작성됩니다.
$$ E = \ int _ {-\ infty} ^ {+ \ infty} x ^ {2} (t) dt $$에너지 유형 신호의 스펙트럼 밀도는 다양한 주파수 수준에서 분산 된 에너지의 양을 제공합니다.
전원 유형 신호
신호는 정규화 된 평균 전력이 유한하고 0이 아닌 경우 (0 <p <∞) 인 경우에만 전력 유형 신호라고합니다. 전력 유형 신호의 경우 정규화 된 평균 전력은 유한하고 0이 아닙니다. 거의 모든 주기적 신호는 전력 신호이며 평균 전력은 유한하고 0이 아닙니다.
수학적 형식에서 신호 x (t)의 거듭 제곱은 다음과 같이 쓸 수 있습니다.
$$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {-T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$에너지와 전력 신호의 차이
다음 표에는 에너지 및 전력 신호의 차이점이 요약되어 있습니다.
| 전원 신호 | 에너지 신호 |
|---|---|
| 실제 주기적 신호는 전력 신호입니다. | 비 주기적 신호는 에너지 신호입니다. |
| 여기서 정규화 된 평균 전력은 유한하고 0이 아닙니다. | 여기서 총 정규화 된 에너지는 유한하고 0이 아닙니다. |
|
수학적으로 $$ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {-T / 2} ^ {+ T / 2} x ^ {2} (t) dt $$ |
수학적으로 $$ E = \ int _ {-\ infty} ^ {+ \ infty} x ^ {2} (t) dt $$ |
| 이러한 신호의 존재는 시간이 지남에 따라 무한합니다. | 이러한 신호는 제한된 기간 동안 존재합니다. |
| 전력 신호의 에너지는 무한한 시간에 무한합니다. | 에너지 신호의 전력은 무한한 시간 동안 0입니다. |
해결 된 예
Example 1 − 신호의 거듭 제곱 구하기 $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $
Solution− 위의 두 신호는 주파수 항이 서로 동일하고 위상차도 동일하기 때문에 서로 직교합니다. 따라서 총 권력은 개별 권력의 합이 될 것입니다.
$ z (t) = x (t) + y (t) $
$ x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ 및 $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $
$ x (t)의 거듭 제곱 = \ frac {2 ^ {2}} {2} = 2 $
$ y (t)의 거듭 제곱 = \ frac {4 ^ {2}} {2} = 8 $
따라서 $ P (z) = p (x) + p (y) = 2 + 8 = 10 $ … Ans.
Example 2 − $ x (t) = t ^ {2} + j \ sin t $에 주어진 신호가 켤레인지 여부를 테스트합니까?
Solution- 여기, 실제 부품의 존재의 t 2 $ \ 죄 t $으로 홀수 인 짝수 및 홀수 부분 (가상)입니다. 따라서 위의 신호는 Conjugate 신호입니다.
Example 3 − $ X (t) = \ sin \ omega t $가 홀수 신호인지 짝수 신호인지 확인합니다.
Solution − 주어진 $ X (t) = \ sin \ omega t $
시간 반전으로 $ \ sin (-\ omega t) $
그러나 우리는 $ \ sin (-\ phi) =-\ sin \ phi $라는 것을 알고 있습니다.
따라서,
$$ \ sin (-\ omega t) =-\ sin \ omega t $$이것은 신호가 홀수 인 조건을 만족합니다. 따라서 $ \ sin \ omega t $는 홀수 신호입니다.