Prinsip Divisi Kuantitas Listrik
Dalam bab ini, mari kita bahas tentang dua prinsip pembagian besaran listrik berikut.
- Prinsip Divisi Saat Ini
- Prinsip Divisi Tegangan
Prinsip Divisi Saat Ini
Ketika dua atau lebih elemen pasif dihubungkan secara paralel, jumlah arus yang mengalir melalui setiap elemen didapat divided (dibagi) di antara mereka sendiri dari arus yang memasuki node.
Simak berikut ini circuit diagram.
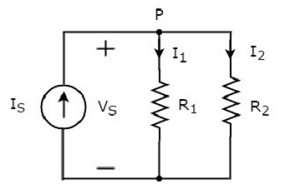
Diagram rangkaian di atas terdiri dari sumber arus masukan IS secara paralel dengan dua resistor R1 dan R2. Tegangan di setiap elemen adalahVS. Arus mengalir melalui resistorR1 dan R2 adalah I1 dan I2 masing-masing.
Itu KCL equation di node P akan
$$ I_S = I_1 + I_2 $$
Gantikan $ I_1 = \ frac {V_S} {R_1} $ dan $ I_2 = \ frac {V_S} {R_2} $ dalam persamaan di atas.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$
Gantikan nilai V S ke $ I_1 = \ frac {V_S} {R_1} $.
$$ I_1 = \ frac {I_S} {R_1} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Gantikan nilai V S menjadi $ I_2 = \ frac {V_S} {R_2} $.
$$ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Dari persamaan I 1 dan I 2 , kita dapat menggeneralisasi bahwa arus yang mengalir melalui elemen pasif dapat diketahui dengan menggunakan rumus berikut.
$$ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert ... \ rVert Z_ {N-1}} {Z_1 + Z_2 + ... + Z_N} \ rgroup $$
Ini dikenal sebagai current division principle dan itu berlaku, ketika dua atau lebih elemen pasif dihubungkan secara paralel dan hanya satu arus yang masuk ke node.
Dimana,
Aku N adalah arus yang mengalir melalui elemen pasif N th cabang.
I S adalah arus masukan, yang memasuki node.
Z 1 , Z 2 , ..., Z N adalah impedansi dari 1 st cabang, 2 nd cabang, ..., N th cabang masing-masing.
Prinsip Divisi Tegangan
Ketika dua atau lebih elemen pasif dihubungkan secara seri, jumlah tegangan yang ada di setiap elemen didapat divided (dibagi) di antara mereka sendiri dari tegangan yang tersedia di seluruh kombinasi itu.
Simak berikut ini circuit diagram.
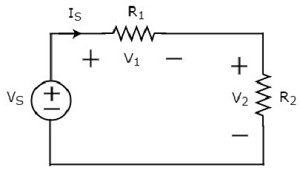
Diagram rangkaian di atas terdiri dari sumber tegangan, V S secara seri dengan dua resistor R 1 dan R 2 . Arus yang mengalir melalui elemen-elemen ini adalah saya S . Tegangan turun di resistor R 1 dan R 2 adalah V 1 dan V 2 masing-masing.
Itu KVL equation sekitar loop akan
$$ V_S = V_1 + V_2 $$
Substitusi V 1 = I S R 1 dan V 2 = I S R 2 pada persamaan di atas
$$ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $$
$$ I_S = \ frac {V_S} {R_1 + R_2} $$
Gantikan nilai I S di V 1 = I S R 1 .
$$ V_1 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_1 $$
$$ \ Rightarrow V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Gantikan nilai I S di V 2 = I S R 2 .
$$ V_2 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_2 $$
$$ \ Rightarrow V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Dari persamaan V 1 dan V 2 , kita dapat menggeneralisasi bahwa tegangan di semua elemen pasif dapat ditemukan dengan menggunakan rumus berikut.
$$ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + .... + Z_N} \ rgroup $$
Ini dikenal sebagai voltage division principle dan itu berlaku, ketika dua atau lebih elemen pasif dihubungkan secara seri dan hanya satu voltase tersedia di seluruh kombinasi.
Dimana,
V N adalah tegangan yang melintasi elemen pasif ke- N .
V S adalah tegangan input, yang ada di seluruh kombinasi elemen pasif seri.
Z 1 , Z 2 , ..., Z 3 adalah impedansi dari 1 st elemen pasif, 2 nd elemen pasif, ..., N th elemen pasif masing-masing.