Teori Jaringan - Teorema Thevenin
Thevenin’s theoremmenyatakan bahwa setiap dua jaringan atau rangkaian linier terminal dapat diwakili dengan jaringan atau rangkaian ekivalen, yang terdiri dari sumber tegangan secara seri dengan resistor. Ini dikenal sebagai sirkuit ekivalen Thevenin. Sirkuit linier dapat berisi sumber independen, sumber dependen, dan resistor.
Jika rangkaian berisi beberapa sumber independen, sumber dependen, dan resistor, maka respons dalam suatu elemen dapat dengan mudah ditemukan dengan mengganti seluruh jaringan di sebelah kiri elemen itu dengan a Thevenin’s equivalent circuit.
Itu response in an element dapat berupa tegangan melintasi elemen itu, arus yang mengalir melalui elemen itu, atau daya yang dihamburkan melintasi elemen itu.
Konsep ini diilustrasikan pada gambar berikut.
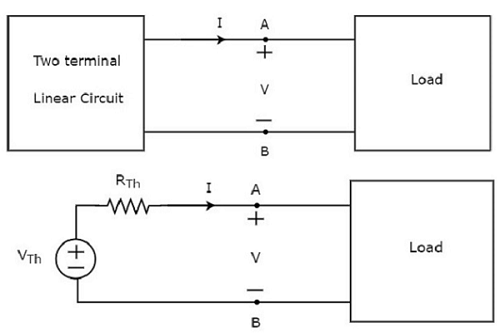
Thevenin’s equivalent circuitmenyerupai sumber tegangan praktis. Oleh karena itu, ia memiliki sumber tegangan secara seri dengan resistor.
Sumber tegangan yang ada di rangkaian ekivalen Thevenin disebut sebagai tegangan ekivalen Thevenin atau sederhananya Thevenin’s voltage, VTh.
Resistor yang ada dalam rangkaian ekivalen Thevenin disebut sebagai resistor ekivalen Thevenin atau sederhananya Thevenin’s resistor, RTh.
Metode untuk Menemukan Sirkuit Ekuivalen Thevenin
Ada tiga metode untuk menemukan rangkaian ekivalen Thevenin. Berdasarkantype of sourcesyang ada di jaringan, kita dapat memilih salah satu dari tiga metode ini. Sekarang, mari kita bahas dua metode satu per satu. Kami akan membahas metode ketiga di bab berikutnya.
Metode 1
Ikuti langkah-langkah ini untuk menemukan rangkaian ekivalen Thevenin, jika hanya sources of independent type hadir.
Step 1 - Pertimbangkan diagram sirkuit dengan membuka terminal yang berkenaan dengan sirkuit ekivalen Thevenin.
Step 2 - Temukan voltase Thevenin VTh melintasi terminal terbuka dari sirkuit di atas.
Step 3 - Temukan perlawanan Thevenin RTh melintasi terminal terbuka dari rangkaian di atas dengan menghilangkan sumber independen yang ada di dalamnya.
Step 4 - Gambarlah Thevenin’s equivalent circuitdengan menghubungkan tegangan Thevenin V Th secara seri dengan resistansi Thevenin R Th .
Sekarang, kita dapat menemukan respons dalam elemen yang terletak di sisi kanan rangkaian ekivalen Thevenin.
Contoh
Temukan arus yang mengalir melalui resistor 20 Ω dengan cara mencari a Thevenin’s equivalent circuit di sebelah kiri terminal A dan B.
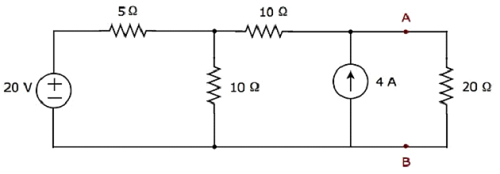
Step 1 - Untuk menemukan rangkaian ekivalen Thevenin di sisi kiri terminal A & B, kita harus melepaskan resistor 20 Ω dari jaringan dengan opening the terminals A & B. Diagram rangkaian yang dimodifikasi ditunjukkan pada gambar berikut.
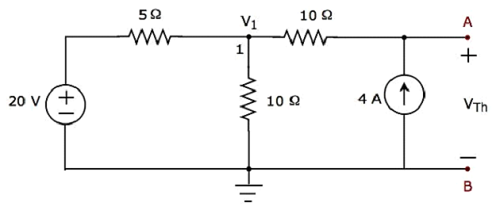
Step 2 - Perhitungan Thevenin’s voltage VTh.
Hanya ada satu node utama kecuali Ground di sirkuit di atas. Jadi, kita bisa menggunakannodal analysismetode. Tegangan node V 1 dan tegangan Thevenin V Th diberi label pada gambar di atas. Di sini, V 1 adalah tegangan dari node 1 terhadap Ground dan V Th adalah tegangan pada sumber arus 4 A.
Itu nodal equation di node 1 adalah
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} - 4 = 0 $$
$$ \ Rightarrow \ frac {2V_1 - 40 + V_1 - 40} {10} = 0 $$
$$ \ Rightarrow 3V_1 - 80 = 0 $$
$$ \ Rightarrow V_1 = \ frac {80} {3} V $$
Tegangan pada resistor 10 Ω cabang seri adalah
$$ V_ {10 \ Omega} = (-4) (10) = -40V $$
Ada dua mata jaring di sirkuit di atas. ItuKVL equation sekitar jala kedua
$$ V_1 - V_ {10 \ Omega} - V_ {Th} = 0 $$
Gantikan nilai $ V_1 $ dan $ V_ {10 \ Omega} $ dalam persamaan di atas.
$$ \ frac {80} {3} - (-40) - V_ {Th} = 0 $$
$$ V_ {Th} = \ frac {80 + 120} {3} = \ frac {200} {3} V $$
Oleh karena itu, tegangan Thevenin adalah $ V_ {Th} = \ frac {200} {3} V $
Step 3 - Perhitungan Thevenin’s resistance RTh.
Hubung singkat sumber tegangan dan hubung -singkatkan sumber arus dari rangkaian di atas untuk menghitung resistansi Thevenin R Th melintasi terminal A & B.modified circuit diagram ditunjukkan pada gambar berikut.
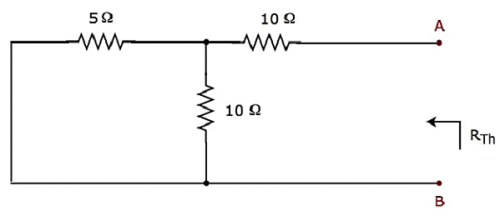
Resistensi Thevenin di terminal A & B akan terjadi
$$ R_ {Th} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
Oleh karena itu, hambatan Thevenin adalah $ \ mathbf {R_ {Th} = \ frac {40} {3} \ Omega} $.
Step 4- Sirkuit ekivalen Thevenin ditempatkan di sebelah kiri terminal A & B pada sirkuit yang diberikan. Diagram sirkuit ini ditunjukkan pada gambar berikut.

Arus yang mengalir melalui resistor 20 Ω dapat diketahui dengan mensubstitusi nilai V Th , R Th dan R pada persamaan berikut.
$$ l = \ frac {V_ {Th}} {R_ {Th} + R} $$
$$ l = \ frac {\ frac {200} {3}} {\ frac {40} {3} + 20} = \ frac {200} {100} = 2A $$
Oleh karena itu, arus yang mengalir melalui resistor 20 Ω adalah 2 A.
Metode 2
Ikuti langkah-langkah ini untuk menemukan rangkaian ekivalen Thevenin, saat sources of both independent type and dependent type hadir.
Step 1 - Pertimbangkan diagram sirkuit dengan membuka terminal yang dengannya, sirkuit ekivalen Thevenin dapat ditemukan.
Step 2 - Temukan voltase Thevenin VTh melintasi terminal terbuka dari sirkuit di atas.
Step 3 - Temukan arus hubung singkat ISC dengan korsleting dua terminal terbuka dari sirkuit di atas.
Step 4 - Temukan perlawanan Thevenin RTh dengan menggunakan rumus berikut.
$$ R_ {Th} = \ frac {V_ {Th}} {I_ {SC}} $$
Step 5 - Gambarlah Thevenin’s equivalent circuitdengan menghubungkan tegangan Thevenin V Th secara seri dengan resistansi Thevenin R Th .
Sekarang, kita dapat menemukan respons dalam elemen yang terletak di sisi kanan rangkaian ekivalen Thevenin.