Teori Jaringan - Jaringan Dua Port
Secara umum, mudah untuk menganalisis jaringan listrik apa pun, jika direpresentasikan dengan model yang setara, yang memberikan hubungan antara variabel input dan output. Untuk ini, kita bisa menggunakantwo port networkrepresentasi. Seperti namanya, dua jaringan port berisi dua port. Diantaranya, satu port digunakan sebagai port input dan port lainnya digunakan sebagai port output. Port pertama dan kedua masing-masing disebut sebagai port1 dan port2.
One port networkadalah jaringan listrik dua terminal di mana arus masuk melalui satu terminal dan keluar melalui terminal lain. Resistor, induktor, dan kapasitor adalah contoh dari satu jaringan port karena masing-masing memiliki dua terminal. Representasi jaringan satu port ditunjukkan pada gambar berikut.
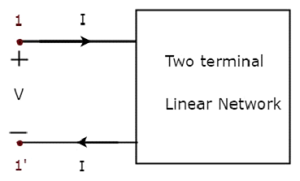
Di sini, pasangan terminal, 1 & 1 'mewakili sebuah port. Dalam kasus ini, kami hanya memiliki satu port karena ini adalah jaringan satu port.
Demikian pula, two port networkadalah sepasang jaringan listrik dua terminal di mana arus masuk melalui satu terminal dan keluar melalui terminal lain dari setiap port. Representasi jaringan dua port ditunjukkan pada gambar berikut.
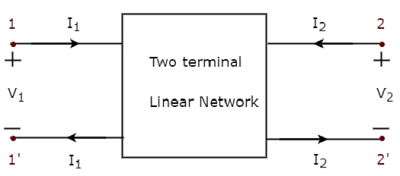
Di sini, sepasang terminal, 1 & 1 'mewakili satu port, yang disebut sebagai port1 dan pasangan terminal lainnya, 2 & 2 'mewakili port lain, yang disebut sebagai port2.
Ada four variablesV 1 , V 2 , I 1 dan I 2 dalam jaringan dua port seperti yang ditunjukkan pada gambar. Dari situ, kita dapat memilih dua variabel sebagai independen dan dua variabel lainnya sebagai dependen. Jadi, kita akan mendapatkan enam kemungkinan pasang persamaan. Persamaan ini merepresentasikan variabel dependen dalam istilah variabel independen. Koefisien variabel independen disebut sebagaiparameters. Jadi, setiap pasangan persamaan akan memberikan satu set empat parameter.
Dua Parameter Jaringan Port
Parameter jaringan dua port disebut sebagai two port network parametersatau sederhananya, dua parameter port. Berikut adalah jenis dari dua parameter jaringan port.
- Parameter Z.
- Parameter Y
- Parameter T.
- Parameter T '
- h-parameters
- g-parameters
Sekarang, mari kita bahas tentang dua parameter jaringan port ini satu per satu.
Parameter Z.
Kita akan mendapatkan dua persamaan berikut dengan menganggap variabel V 1 & V 2 sebagai dependen dan I 1 & I 2 sebagai variabel independen. Koefisien variabel independen, I 1 dan I 2 disebut sebagaiZ parameters.
$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$
$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$
Itu Z parameters adalah
$$ Z_ {11} = \ frac {V_1} {I_1}, \: saat \: I_2 = 0 $$
$$ Z_ {12} = \ frac {V_1} {I_2}, \: ketika \: I_1 = 0 $$
$$ Z_ {21} = \ frac {V_2} {I_1}, \: ketika \: I_2 = 0 $$
$$ Z_ {22} = \ frac {V_2} {I_2}, \: ketika \: I_1 = 0 $$
Parameter Z disebut sebagai impedance parameterskarena ini hanyalah rasio tegangan dan arus. Satuan parameter Z adalah Ohm (Ω).
Kita dapat menghitung dua parameter Z, Z 11 dan Z 21 , dengan melakukan rangkaian terbuka pada port2. Demikian pula, kita dapat menghitung dua parameter Z lainnya, Z 12 dan Z 22 dengan melakukan rangkaian terbuka pada port1. Oleh karena itu, parameter Z juga disebut sebagaiopen-circuit impedance parameters.
Parameter Y
Kita akan mendapatkan dua persamaan berikut dengan mempertimbangkan variabel I 1 & I 2 sebagai dependen dan V 1 & V 2 sebagai variabel independen. Koefisien variabel independen, V 1 dan V 2 disebut sebagaiY parameters.
$$ I_1 = Y_ {11} V_1 + Y_ {12} V_2 $$
$$ I_2 = Y_ {21} V_1 + Y_ {22} V_2 $$
Itu Y parameters adalah
$$ Y_ {11} = \ frac {I_1} {V_1}, \: when \: V_2 = 0 $$
$$ Y_ {12} = \ frac {I_1} {V_2}, \: when \: V_1 = 0 $$
$$ Y_ {21} = \ frac {I_2} {V_1}, \: when \: V_2 = 0 $$
$$ Y_ {22} = \ frac {I_2} {V_2}, \: when \: V_1 = 0 $$
Parameter Y disebut sebagai admittance parameterskarena ini hanyalah rasio arus dan tegangan. Satuan parameter Y adalah mho.
Kita dapat menghitung dua parameter Y, Y 11 dan Y 21 dengan melakukan hubung singkat pada port2. Demikian pula, kita dapat menghitung dua parameter Y lainnya, Y 12 dan Y 22 dengan melakukan hubung singkat pada port1. Oleh karena itu, parameter Y juga disebut sebagaishort-circuit admittance parameters.
Parameter T.
Kita akan mendapatkan dua persamaan berikut dengan menganggap variabel V 1 & I 1 sebagai dependen dan V 2 & I 2 sebagai variabel independen. Koefisien dari V 2 dan -I 2 disebut sebagaiT parameters.
$$ V_1 = A V_2 - B I_2 $$
$$ I_1 = C V_2 - D I_2 $$
Itu T parameters adalah
$$ A = \ frac {V_1} {V_2}, \: saat \: I_2 = 0 $$
$$ B = - \ frac {V_1} {I_2}, \: when \: V_2 = 0 $$
$$ C = \ frac {I_1} {V_2}, \: when \: I_2 = 0 $$
$$ D = - \ frac {I_1} {I_2}, \: when \: V_2 = 0 $$
Parameter T disebut sebagai parameter transmisi atau ABCD parameters. Parameter, A dan D tidak memiliki satuan apapun, karena dimensinya lebih kecil. Satuan parameter, B dan C masing-masing adalah ohm dan mho.
Kita dapat menghitung dua parameter, A dan C dengan melakukan rangkaian terbuka pada port2. Demikian pula, kita dapat menghitung dua parameter lainnya, B dan D dengan melakukan hubung singkat pada port2.
Parameter T '
Kita akan mendapatkan himpunan dua persamaan berikut dengan menganggap variabel V 2 & I 2 sebagai dependen dan V 1 & I 1 sebagai independen. Koefisien dari V 1 dan -I 1 disebut sebagaiT’ parameters.
$$ V_2 = A 'V_1 - B' I_1 $$
$$ I_2 = C 'V_1 - D' I_1 $$
Itu T’ parameters adalah
$$ A '= \ frac {V_2} {V_1}, \: when \: I_1 = 0 $$
$$ B '= - \ frac {V_2} {I_1}, \: when \: V_1 = 0 $$
$$ C '= \ frac {I_2} {V_1}, \: when \: I_1 = 0 $$
$$ D '= - \ frac {I_2} {I_1}, \: when \: V_1 = 0 $$
Parameter T 'disebut sebagai parameter transmisi terbalik atau A’B’C’D’ parameters. Parameter A 'dan D' tidak memiliki satuan apapun, karena dimensinya lebih kecil. Satuan parameter, B 'dan C', masing-masing adalah Ohm dan Mho.
Kita dapat menghitung dua parameter, A 'dan C', dengan melakukan rangkaian terbuka pada port1. Demikian pula, kita dapat menghitung dua parameter lainnya, B 'dan D', dengan melakukan hubung singkat pada port1.
h-parameter
Kita akan mendapatkan dua persamaan berikut dengan mempertimbangkan variabel V 1 & I 2 sebagai dependen dan I 1 & V 2 sebagai variabel independen. Koefisien variabel independen, I 1 dan V 2 , disebut sebagaih-parameters.
$$ V_1 = h_ {11} I_1 + h_ {12} V_2 $$
$$ I_2 = h_ {21} I_1 + h_ {22} V_2 $$
Parameter h adalah
$$ h_ {11} = \ frac {V_1} {I_1}, \: when \: V_2 = 0 $$
$$ h_ {12} = \ frac {V_1} {V_2}, \: when \: I_1 = 0 $$
$$ h_ {21} = \ frac {I_2} {I_1}, \: when \: V_2 = 0 $$
$$ h_ {22} = \ frac {I_2} {V_2}, \: when \: I_1 = 0 $$
h-parameter disebut sebagai hybrid parameters. Parameternya, h 12 dan h 21 , tidak memiliki satuan apa pun, karena tidak berdimensi. Satuan parameter, h 11 dan h 22 , masing-masing adalah Ohm dan Mho.
Kita dapat menghitung dua parameter, h 11 dan h 21 dengan melakukan hubung singkat port2. Demikian pula, kita dapat menghitung dua parameter lainnya, h 12 dan h 22 dengan melakukan rangkaian terbuka port1.
Parameter h atau parameter hybrid berguna dalam rangkaian pemodelan transistor (jaringan).
g-parameter
Kita akan mendapatkan dua persamaan berikut dengan menganggap variabel I 1 & V 2 sebagai dependen dan V 1 & I 2 sebagai variabel independen. Koefisien variabel independen, V 1 dan I 2 disebut sebagaig-parameters.
$$ I_1 = g_ {11} V_1 + g_ {12} I_2 $$
$$ V_2 = g_ {21} V_1 + g_ {22} I_2 $$
Itu g-parameters adalah
$$ g_ {11} = \ frac {I_1} {V_1}, \: when \: I_2 = 0 $$
$$ g_ {12} = \ frac {I_1} {I_2}, \: when \: V_1 = 0 $$
$$ g_ {21} = \ frac {V_2} {V_1}, \: ketika \: I_2 = 0 $$
$$ g_ {22} = \ frac {V_2} {I_2}, \: when \: V_1 = 0 $$
g-parameter disebut sebagai inverse hybrid parameters. Parameter, g 12 dan g 21 tidak memiliki satuan apapun, karena dimensinya lebih kecil. Satuan parameter, g 11 dan g 22 masing-masing adalah mho dan ohm.
Kita dapat menghitung dua parameter, g 11 dan g 21 dengan melakukan rangkaian terbuka pada port2. Demikian pula, kita dapat menghitung dua parameter lainnya, g 12 dan g 22 dengan melakukan hubung singkat port1.