Teori Jaringan - Konversi Bintang ke Delta
Pada bab sebelumnya kita telah membahas tentang konversi jaringan delta menjadi jaringan bintang yang setara. Sekarang, mari kita bahas tentang konversi jaringan bintang menjadi jaringan delta yang setara. Konversi ini disebut sebagaiStar to Delta Conversion.
Di bab sebelumnya, kami mendapatkan file resistances of star network dari jaringan delta sebagai
$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ Equation 3
Resistensi Jaringan Delta dalam hal Resistensi Jaringan Star
Mari kita manipulasi persamaan di atas untuk mendapatkan resistansi jaringan delta dalam hal resistansi jaringan star.
Multiply setiap set dari dua persamaan dan kemudian add.
$$ R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 ^ 2 R_3 + R_2 R_3 ^ 2 R_1 + R_3 R_1 ^ 2 R_2} {(R_1 + R_2 + R_3) ^ 2} $$
$$ \ Sisi Kanan R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3 (R_1 + R_2 + R_3)} {(R_1 + R_2 + R_3) ^ 2} $$
$ \ Panah Kanan R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3} {R_1 + R_2 + R_3} $ Equation 4
Dengan membagi Persamaan 4 dengan Persamaan 2, kita akan mendapatkan
$$ \ frac {R_A R_B + R_B R_C + R_C R_A} {R_B} = R_1 $$
$$ \ Rightarrow R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
Dengan membagi Persamaan 4 dengan Persamaan 3, kita akan mendapatkan
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
Dengan membagi Persamaan 4 dengan Persamaan 1, kita akan mendapatkan
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
Dengan menggunakan relasi di atas, kita dapat mengetahui resistansi jaringan delta dari resistansi jaringan star. Dengan cara ini, kita bisa bertobatstar network into delta network.
Contoh
Mari kita hitung resistances of delta network, yang setara dengan jaringan bintang seperti yang ditunjukkan pada gambar berikut.
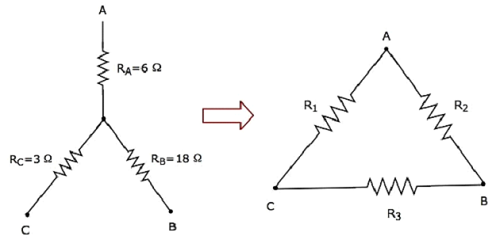
Mengingat resistances of star networksebagai R A = 6 Ω, R B = 18 Ω dan R C = 3 Ω .
Kami tahu hubungan berikut dari resistances of delta network dalam hal resistensi jaringan bintang.
$$ R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
Gantikan nilai R A , R B, dan R C dalam persamaan di atas.
$$ R_1 = 3 + 6 + \ frac {3 \ times 6} {18} = 9 + 1 = 10 \ Omega $$
$$ R_2 = 6 + 18 + \ frac {6 \ times 18} {3} = 24 + 36 = 60 \ Omega $$
$$ R_3 = 18 + 3 + \ frac {18 \ times 3} {6} = 21 + 9 = 30 \ Omega $$
Jadi, kami mendapat resistansi jaringan delta sebagai R1 = 10 Ω, R2 = 60 Ω dan R3 = 30 Ω, yang setara dengan resistansi jaringan bintang yang diberikan.