Teori Jaringan - Topologi Jaringan
Topologi jaringan adalah representasi grafis dari rangkaian listrik. Ini berguna untuk menganalisis rangkaian listrik yang kompleks dengan mengubahnya menjadi grafik jaringan. Topologi jaringan juga disebut sebagaiGraph theory.
Terminologi Dasar Topologi Jaringan
Sekarang, mari kita bahas tentang terminologi dasar yang terlibat dalam topologi jaringan ini.
Grafik
Grafik jaringan disebut sebagai graph. Ini terdiri dari satu set node yang dihubungkan oleh cabang. Dalam grafik, node adalah titik persekutuan dari dua cabang atau lebih. Terkadang, hanya satu cabang yang dapat terhubung ke node. Cabang adalah ruas garis yang menghubungkan dua node.
Sirkuit atau jaringan listrik apa pun dapat diubah menjadi padanannya graphdengan mengganti elemen pasif dan sumber tegangan dengan hubung singkat dan sumber arus dengan rangkaian terbuka. Artinya, segmen garis pada grafik mewakili cabang-cabang yang berhubungan dengan elemen pasif atau sumber tegangan rangkaian listrik.
Contoh
Mari kita simak berikut ini electric circuit.
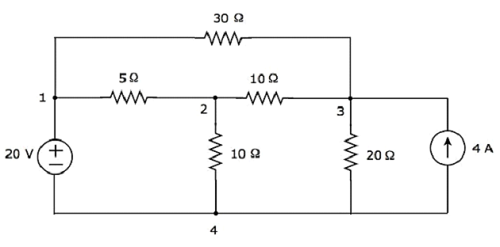
Di sirkuit di atas, ada four principal nodes dan yang diberi label 1, 2, 3, dan 4. Ada seven branches pada rangkaian di atas, di antaranya satu cabang berisi sumber tegangan 20 V, cabang lain berisi sumber arus 4 A dan lima cabang lainnya berisi resistor yang masing-masing memiliki resistansi 30 Ω, 5 Ω, 10 Ω, 10 Ω dan 20 Ω.
Setara graph sesuai dengan rangkaian listrik di atas ditunjukkan pada gambar berikut.
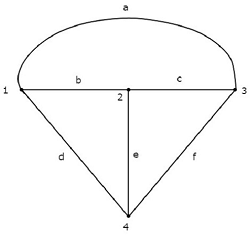
Pada grafik di atas, ada four nodesdan masing-masing diberi label dengan 1, 2, 3 & 4. Ini sama dengan node utama dalam rangkaian listrik. Adasix branches pada grafik di atas dan masing-masing diberi label dengan a, b, c, d, e & f.
Dalam hal ini, kami mendapat one branch less dalam grafik karena sumber arus 4 A dibuat sebagai rangkaian terbuka, sekaligus mengubah rangkaian listrik menjadi grafik ekuivalennya.
Dari Contoh ini, kita dapat menyimpulkan poin-poin berikut -
Itu number of nodes hadir dalam grafik akan sama dengan jumlah node utama yang ada dalam rangkaian listrik.
Itu number of branches hadir dalam grafik akan kurang dari atau sama dengan jumlah cabang yang ada dalam rangkaian listrik.
Jenis Grafik
Berikut adalah jenis-jenis grafiknya -
- Grafik Terhubung
- Grafik Tidak Terhubung
- Grafik Berarah
- Grafik Tidak Berarah
Sekarang, mari kita bahas grafik tersebut satu per satu.
Grafik Terhubung
Jika terdapat setidaknya satu cabang antara salah satu dari dua node grafik, maka itu disebut sebagai a connected graph. Artinya, setiap node pada graph yang terhubung akan memiliki satu atau lebih cabang yang terhubung dengannya. Jadi, tidak ada node yang akan ditampilkan sebagai terisolasi atau terpisah.
Grafik yang ditunjukkan pada Contoh sebelumnya adalah a connected graph. Di sini, semua node dihubungkan oleh tiga cabang.
Grafik Tidak Terhubung
Jika terdapat setidaknya satu node dalam grafik yang tetap tidak terhubung bahkan oleh satu cabang, maka itu disebut sebagai unconnected graph. Jadi, akan ada satu atau lebih node yang terisolasi dalam grafik yang tidak terhubung.
Perhatikan grafik yang ditunjukkan pada gambar berikut.
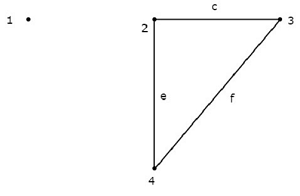
Pada grafik ini, node 2, 3, dan 4 dihubungkan oleh dua cabang masing-masing. Tapi, tidak ada satu pun cabang yang terhubung kenode 1. Jadi, simpul 1 menjadiisolated node. Oleh karena itu, grafik di atas adalahunconnected graph.
Grafik Berarah
Jika semua cabang dari suatu grafik diwakili oleh panah, maka grafik tersebut disebut sebagai a directed graph. Tanda panah ini menunjukkan arah aliran arus di setiap cabang. Karenanya, grafik ini juga disebut sebagaioriented graph.
Perhatikan grafik yang ditunjukkan pada gambar berikut.
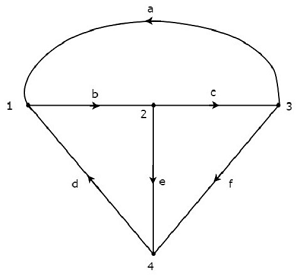
Pada grafik di atas, arah aliran arus direpresentasikan dengan panah di setiap cabang. Oleh karena itu, ini adalah adirected graph.
Grafik Tidak Berarah
Jika cabang dari suatu grafik tidak diwakili oleh panah, maka grafik tersebut disebut sebagai undirected graph. Karena tidak ada arah aliran arus, grafik ini disebut juga sebagaiunoriented graph.
Grafik yang ditunjukkan pada Contoh pertama bab ini adalah unoriented graph, karena tidak ada panah di cabang grafik itu.
Subgraf dan Jenisnya
Bagian dari grafik disebut sebagai a subgraph. Kami mendapatkan subgraf dengan menghapus beberapa node dan / atau cabang dari grafik tertentu. Jadi, jumlah cabang dan / atau node subgraf akan lebih sedikit dari graf aslinya. Oleh karena itu, kita dapat menyimpulkan bahwa subgraf adalah himpunan bagian dari grafik.
Berikut ini adalah two types dari subgraf.
- Tree
- Co-Tree
Pohon
Pohon adalah subgraf terhubung dari grafik tertentu, yang berisi semua node dari grafik. Tapi, seharusnya tidak ada loop apa pun di subgraf itu. Cabang-cabang pohon disebut sebagaitwigs.
Simak berikut ini connected subgraph grafik, yang ditunjukkan pada Contoh di awal bab ini.
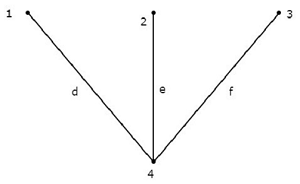
Subgraf yang terhubung ini berisi keempat node dari grafik yang diberikan dan tidak ada loop. Oleh karena itu, ini adalah aTree.
Pohon ini hanya memiliki tiga cabang dari enam cabang grafik yang diberikan. Karena, jika kita menganggap bahkan satu cabang dari cabang grafik yang tersisa, maka akan ada loop pada subgraf yang terhubung di atas. Kemudian, subgraf terhubung yang dihasilkan tidak akan menjadi Pohon.
Dari Pohon di atas, kita dapat menyimpulkan bahwa number of branches yang ada di Pohon harus sama dengan n - 1 di mana 'n' adalah jumlah node dari grafik yang diberikan.
Co-Tree
Co-Tree adalah subgraf, yang dibentuk dengan cabang-cabang yang dibuang saat membentuk Pohon. Oleh karena itu, disebut sebagaiComplementdari Pohon. Untuk setiap Pohon, akan ada Co-Tree yang sesuai dan cabangnya disebut sebagailinksatau akord. Secara umum, tautan direpresentasikan dengan garis putus-putus.
Itu Co-Tree sesuai dengan Pohon di atas ditunjukkan pada gambar berikut.
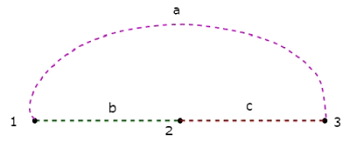
Co-Tree ini hanya memiliki tiga node, bukan empat node dari grafik yang diberikan, karena Node 4 diisolasi dari Co-Tree di atas. Oleh karena itu, Co-Tree tidak perlu berupa subgraf yang terhubung. Co-Tree ini memiliki tiga cabang dan membentuk lingkaran.
Itu number of branchesyang ada di pohon pendamping akan sama dengan selisih antara jumlah cabang dari grafik dan jumlah ranting. Secara matematis, dapat ditulis sebagai
$$ l = b - (n - 1) $$
$$ l = b - n + 1 $$
Dimana,
- l adalah jumlah tautan.
- b adalah jumlah cabang yang ada dalam grafik tertentu.
- n adalah jumlah node yang ada dalam grafik tertentu.
Jika kita menggabungkan Pohon dan Co-Tree yang sesuai, maka kita akan mendapatkan file original graph seperti gambar dibawah.
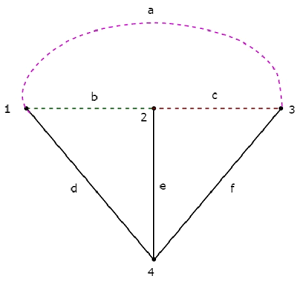
Cabang pohon d, e & f diwakili dengan garis padat. Cabang Co-Tree a, b & c diwakili dengan garis putus-putus.