Teori Jaringan - Respon Sirkuit AC
Pada bab sebelumnya kita telah membahas mengenai respon transient dan respon steady state dari rangkaian DC. Dalam bab ini, mari kita bahasresponse of AC circuit. Konsep respons transient dan respons kondisi tunak, yang telah kita bahas di bab sebelumnya, juga akan berguna di sini.
Menemukan Respon dari Rangkaian RL Seri
Simak berikut ini series RL circuit diagram.

Di sirkuit di atas, switch disimpan opensampai t = 0 dan ditutup pada t = 0 . Jadi, sumber tegangan AC yang memiliki tegangan puncak V m volt tidak tersambung ke rangkaian RL seri hingga saat ini. Karena itu, adano initial current mengalir melalui induktor.
Diagram sirkuit, saat switch masuk closed posisi, ditunjukkan pada gambar berikut.
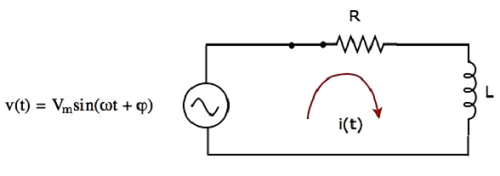
Sekarang, arus i (t) mengalir di seluruh rangkaian, karena sumber tegangan AC yang memiliki tegangan puncak V m volt dihubungkan ke rangkaian RL seri.
Kita tahu bahwa arus i (t) yang mengalir melalui rangkaian di atas akan memiliki dua suku, satu yang mewakili bagian transien dan istilah lainnya mewakili kondisi tunak.
Secara matematis, ini dapat direpresentasikan sebagai
$ i (t) = i_ {Tr} (t) + i_ {ss} (t) $Equation 1
Dimana,
$ i_ {Tr} (t) $ adalah respon transien dari arus yang mengalir melalui rangkaian.
$ i_ {ss} (t) $ adalah respon kondisi tunak dari arus yang mengalir melalui rangkaian.
Pada bab sebelumnya, kita mendapatkan respon transien dari arus yang mengalir melalui rangkaian RL seri. Ini dalam bentuk $ Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $.
Gantikan $ i_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ dalam Persamaan 1.
$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss} (t) $Equation 2
Perhitungan Arus Stabil
Jika sinyal sinusoidal diterapkan sebagai masukan pada rangkaian listrik Linear, maka ia menghasilkan keluaran keadaan tunak, yang juga merupakan a sinusoidal signal. Baik sinyal sinusoidal input maupun output akan memiliki frekuensi yang sama, tetapi amplitudo dan sudut fasa berbeda.
Kita dapat menghitung respon steady state dari suatu rangkaian listrik, ketika digairahkan oleh sumber tegangan sinusoidal menggunakan Laplace Transform approach.
Diagram sirkuit domain-s, ketika switch masuk closed posisi, ditunjukkan pada gambar berikut.
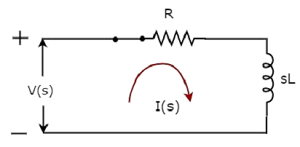
Di sirkuit di atas, semua kuantitas dan parameter diwakili s-domain. Ini adalah transformasi Laplace dari kuantitas dan parameter domain waktu.
Itu Transfer function dari rangkaian di atas adalah
$$ H (s) = \ frac {I (s)} {V (s)} $$
$$ \ Rightarrow H (s) = \ frac {1} {Z (s)} $$
$$ \ Rightarrow H (s) = \ frac {1} {R + sL} $$
Gantikan $ s = j \ omega $ dalam persamaan di atas.
$$ H (j \ omega) = \ frac {1} {R + j \ omega L} $$
Magnitude of $ \ mathbf {\ mathit {H (j \ omega)}} $ adalah
$$ | H (j \ omega) | = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$
Phase angle of $ \ mathbf {\ mathit {H (j \ omega)}} $ adalah
$$ \ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$
Kami akan mendapatkan steady state current $ i_ {ss} (t) $ dengan melakukan dua langkah berikut -
Kalikan tegangan puncak tegangan sinusoidal masukan dan besarnya $ H (j \ omega) $.
Tambahkan sudut fasa tegangan sinusoidal masukan dan $ H (j \ omega) $.
Itu steady state current $ i_ {ss} (t) $ akan menjadi
$$ i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Gantikan nilai $ i_ {ss} (t) $ dalam Persamaan 2.
$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 3
Kita tahu bahwa tidak ada arus awal di sirkuit. Jadi, gantikan t = 0 & i (t) = 0 pada Persamaan 3 untuk mencari nilai konstanta, K.
$$ 0 = Ke ^ {- \ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega (0) + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow K = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Gantikan nilai K dalam Persamaan 3.
$ i (t) = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 4
Persamaan 4 mewakili arus yang mengalir melalui rangkaian RL seri, ketika dieksitasi oleh sumber tegangan sinusoidal. Ini memiliki dua istilah. Suku pertama dan kedua masing-masing mewakili respon transien dan respon kondisi tunak dari arus.
Kita dapat neglect the first termPersamaan 4 karena nilainya akan sangat kurang dari satu. Jadi, arus resultan yang mengalir melalui rangkaian akan menjadi
$$ i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Ini hanya berisi steady state term. Oleh karena itu, kita hanya dapat menemukan respon kondisi tunak dari rangkaian AC dan mengabaikan respon transiennya.