Teori Jaringan - Respon Sirkuit DC

Jika keluaran dari rangkaian listrik untuk suatu masukan bervariasi terhadap waktu, maka itu disebut sebagai time response. Tanggapan waktu terdiri dari dua bagian berikut.

Respon sementara
Respon Stabil

Dalam bab ini, pertama-tama mari kita bahas tentang dua respons ini dan kemudian amati dua respons ini dalam rangkaian RL seri, ketika dieksitasi oleh sumber tegangan DC.

Respon sementara

Setelah menerapkan input ke rangkaian listrik, output membutuhkan waktu tertentu untuk mencapai kondisi tunak. Jadi, output akan berada dalam kondisi transien hingga mencapai kondisi mapan. Oleh karena itu, respons rangkaian listrik selama keadaan transien dikenal sebagaitransient response.

Respon transien akan menjadi nol untuk nilai besar 't'. Idealnya, nilai 't' harus tak terhingga. Tapi, secara praktisfive time constants cukup.

Ada atau Tidak Ada Transien

Transien terjadi dalam respons karena sudden changedalam sumber yang diterapkan ke sirkuit listrik dan / atau karena aksi sakelar. Ada dua kemungkinan tindakan pengalihan. Itu adalah saklar pembuka dan saklar penutup.

Itu transient sebagian akan not presentdalam respons rangkaian listrik atau jaringan, jika hanya berisi resistansi. Karenaresistor adalah memiliki kemampuan untuk menyesuaikan sejumlah tegangan dan arus.
Itu transient part occurs dalam respons rangkaian listrik atau jaringan karena adanya elemen penyimpan energi seperti inductor and capacitor. Karena mereka tidak dapat mengubah energi yang tersimpan dalam elemen tersebut secara instan.

Perilaku Induktor

Asumsikan aksi switching terjadi pada t = 0.Inductor currenttidak berubah secara instan, saat tindakan pengalihan terjadi. Itu berarti, nilai arus induktor tepat setelah tindakan pengalihan akan sama dengan nilai sebelum tindakan pengalihan.

Secara matematis, ini dapat direpresentasikan sebagai

$$ i_L (0 ^ +) = i_L (0 ^ -) $$

Perilaku Kapasitor

Itu capacitor voltagetidak berubah secara instan mirip dengan arus induktor, ketika aksi switching terjadi. Itu berarti, nilai tegangan kapasitor setelah aksi switching akan sama dengan sebelum aksi switching.

Secara matematis, ini dapat direpresentasikan sebagai

$$ v_c (0 ^ +) = v_c (0 ^ -) $$

Respon Stabil

Bagian dari respon waktu yang tersisa bahkan setelah respon transien menjadi nilai nol untuk nilai besar 't' dikenal sebagai steady state response. Artinya, tidak akan ada bagian sementara dalam respons selama kondisi stabil.

Perilaku Induktor

Jika sumber independen dihubungkan ke rangkaian atau jaringan listrik yang memiliki satu atau lebih induktor dan resistor (opsional) dalam waktu yang lama, maka rangkaian atau jaringan listrik tersebut dikatakan dalam keadaan stabil. Oleh karena itu, energi yang disimpan dalam induktor dari rangkaian listrik tersebut adalah maksimum dan konstan.

Secara matematis, ini dapat direpresentasikan sebagai

$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Maksimum & konstan

$ \ Rightarrow i_L = $ Maksimum & konstan

Oleh karena itu, induktor bertindak sebagai a constant current source dalam kondisi mapan.

Tegangan di induktor akan

$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$

Jadi, induktor bertindak sebagai a short circuit dalam kondisi mapan.

Perilaku Kapasitor

Jika sumber independen dihubungkan ke rangkaian atau jaringan listrik yang memiliki satu atau lebih kapasitor dan resistor (opsional) dalam waktu yang lama, maka rangkaian atau jaringan listrik tersebut dikatakan dalam keadaan stabil. Oleh karena itu, energi yang disimpan dalam kapasitor rangkaian listrik tersebut adalah maksimum dan konstan.

Secara matematis, ini dapat direpresentasikan sebagai

$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Maksimum & konstan

$ \ Rightarrow v_c = $ Maksimum & konstan

Oleh karena itu, kapasitor bertindak sebagai a constant voltage source dalam kondisi mapan.

Arus yang mengalir melalui kapasitor akan

$$ i_c = C \ frac {dv_c} {dt} = 0A $$

Jadi, kapasitor bertindak sebagai sebuah open circuit dalam kondisi mapan.

Menemukan Respon dari Rangkaian RL Seri

Simak berikut ini series RL circuit diagram.

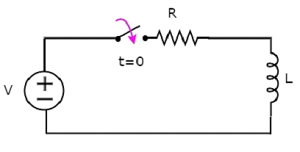
Di sirkuit di atas, switch disimpan openhingga t = 0 dan ditutup pada t = 0. Jadi, sumber tegangan DC yang memiliki V volt tidak terhubung ke rangkaian RL seri hingga saat ini. Oleh karena itu, adano initial current mengalir melalui induktor.

Diagram sirkuit, saat switch masuk closed posisinya ditunjukkan pada gambar berikut.

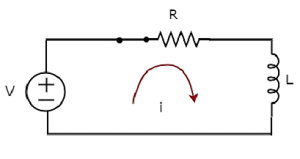
Sekarang, arusnya i mengalir di seluruh rangkaian, karena memiliki sumber tegangan DC V volt terhubung ke rangkaian RL seri.

Sekarang, terapkan KVL di sekitar lingkaran.

$$ V = Ri + L \ frac {di} {dt} $$

$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1

Persamaan di atas adalah persamaan diferensial orde satu dan berbentuk

$ \ frac {dy} {dt} + Py = Q $Equation 2

Oleh comparing Persamaan 1 dan Persamaan 2, kita akan mendapatkan relasi berikut.

$$ x = t $$

$$ y = i $$

$$ P = \ frac {R} {L} $$

$$ Q = \ frac {V} {L} $$

Itu solution dari Persamaan 2 akan

$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3

Dimana, k adalah konstanta.

Gantikan nilai dari x, y, P & Q pada persamaan 3.

$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $

$ \ Rightarrow yaitu ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $

$ \ Rightarrow yaitu ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $

$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4

Kita tahu bahwa tidak ada arus awal di sirkuit. Oleh karena itu, substitusi, t = 0 dan = 0 dalam Persamaan 4 untuk mencari nilai konstanta k.

$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$

$$ 0 = \ frac {V} {R} + k (1) $$

$$ k = - \ frac {V} {R} $$

Gantikan, nilai k dalam Persamaan 4.

$$ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

Oleh karena itu, current mengalir melalui rangkaian tersebut

$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5

Jadi, respons rangkaian RL seri, ketika dieksitasi oleh sumber tegangan DC, memiliki dua istilah berikut.

Suku pertama $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ sesuai dengan transient response.
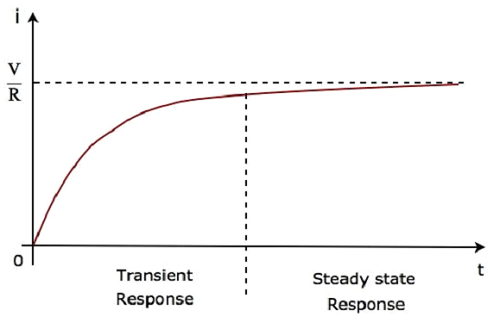
Istilah kedua $ \ frac {V} {R} $ sesuai dengan steady state response. Kedua tanggapan tersebut ditunjukkan pada gambar berikut.

Persamaan 5 dapat ditulis ulang sebagai berikut -

$ i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $

$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6

Dimana, τ adalah time constant dan nilainya sama dengan $ \ frac {L} {R} $.

Persamaan 5 dan Persamaan 6 sama. Tetapi, kita dapat dengan mudah memahami bentuk gelombang arus di atas yang mengalir melalui rangkaian dari Persamaan 6 dengan mengganti beberapa nilait seperti 0, τ, 2τ, 5τ, dll.

Dalam bentuk gelombang arus yang mengalir melalui rangkaian di atas, respons transien akan menampilkan hingga lima konstanta waktu dari nol, sedangkan respons kondisi tunak akan muncul dari lima konstanta waktu dan seterusnya.